Optimizer

机器学习：各种优化器Optimizer的总结与比较

GD(Gradient Descent)

两个缺点:**

• 训练速度慢：每走一步都要要计算调整下一步的方向，下山的速度变慢。需要花费很长时间才能得到收敛解。
• 容易陷入局部最优解：由于是在有限视距内寻找下山的反向。当陷入平坦的洼地，会误以为到达了山地的最低点，从而不会继续往下走。

BGD(Batch Gradient Descent)

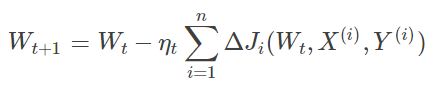
模型参数的调整更新与全部输入样本的代价函数的和（即批量/全局误差）有关。在下山之前掌握了附近的地势情况，选择总体平均梯度最小的方向下山。

SGD(Stochastic Gradient Descent)

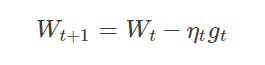
优点：

• 虽然SGD需要走很多步的样子，但是对梯度的要求很低（计算梯度快）。而对于引入噪声，大量的理论和实践工作证明，只要噪声不是特别大，SGD都能很好地收敛。

缺点：

• SGD在随机选择梯度的同时会引入噪声，使得权值更新的方向不一定正确。
• SGD也没能单独克服局部最优解的问题。

**

Momentum（动量优化法）

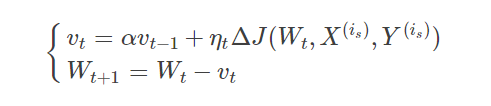
理解策略为：** 由于当前权值的改变会受到上一次权值改变的影响，类似于小球向下滚动的时候带上了惯性。这样可以加快小球向下滚动的速度。
动量主要解决SGD的两个问题：**

• 是随机梯度的方法（引入的噪声）；
• 是Hessian矩阵病态问题（可以理解为SGD在收敛过程中和正确梯度相比来回摆动比较大的问题）。

RMSProp(自适应学习率)

思想：考虑了历史梯度平均值。具有代价函数最大梯度的参数相应地有个小的的学习率，而具有小梯度的参数有个较大的学习率。
RMSProp算法修改了AdaGrad的梯度积累为指数加权的移动平均，使得其在非凸设定下效果更好。
算法描述：RMSProp算法的一般策略可以表示为：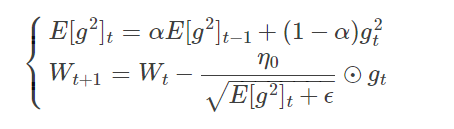

由于取了个加权平均，避免了学习率越来越低的的问题，而且能自适应地调节学习率。

Adam

Adaptive Moment Estimation
Adam 可以认为是 RMSprop 和 Momentum 的结合：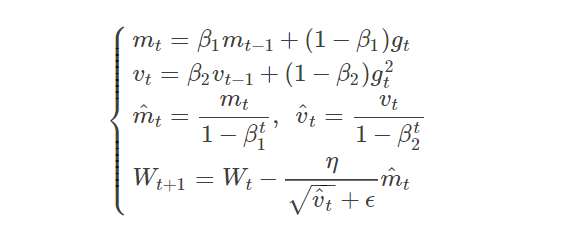

其中，和分别为一阶动量项和二阶动量项。和为动力值大小通常分别取0.9和0.999；和分别为各自的修正值。表示时刻即第迭代模型的参数，表示次迭代代价函数关于的梯度大小；是一个取值很小的数（一般为1e-8）为了避免分母为0.