观察树的图：前中后序遍历的区别就在于根节点的遍历时间的前中后
    默认从左往右，自上而下，所以只有三种

    • 前序遍历：DRL（大树）根——左——右

      （大左子树）根——左——右
      （子子树）根——左——右
      。。。。。。
      （大右子树）根——左——右
      （子子树）根——左——右

    • 中序遍历：RDL
    • 后序遍历：RLD

    观察代码：
    前中后序的原理：三种遍历都是从根结点开始，

    • 前序遍历是先打印再递归左和右。
    • 中序遍历是先递归左再打印后递归右
    • 后序遍历是先递归左和右再打印

    前序遍历：ABDHKECFIGJ

    1. /* 二叉树的前序遍历递归算法 */
    2. void PreOrderTraverse(BiTree T)
    3. {
    4.     if (T == NULL)
    5.         return;
    7.     /* 显示结点数据，可以更改为其他对结点操作 */
    8.     printf("%c", T->data);          
    10.     /* 再先序遍历左子树 */
    11.     PreOrderTraverse(T->lchild);    
    12.     //返回点
    13.     /* 最后先序遍历右子树 */
    14.     PreOrderTraverse(T->rchild);
    15.     //返回点    
    16. }

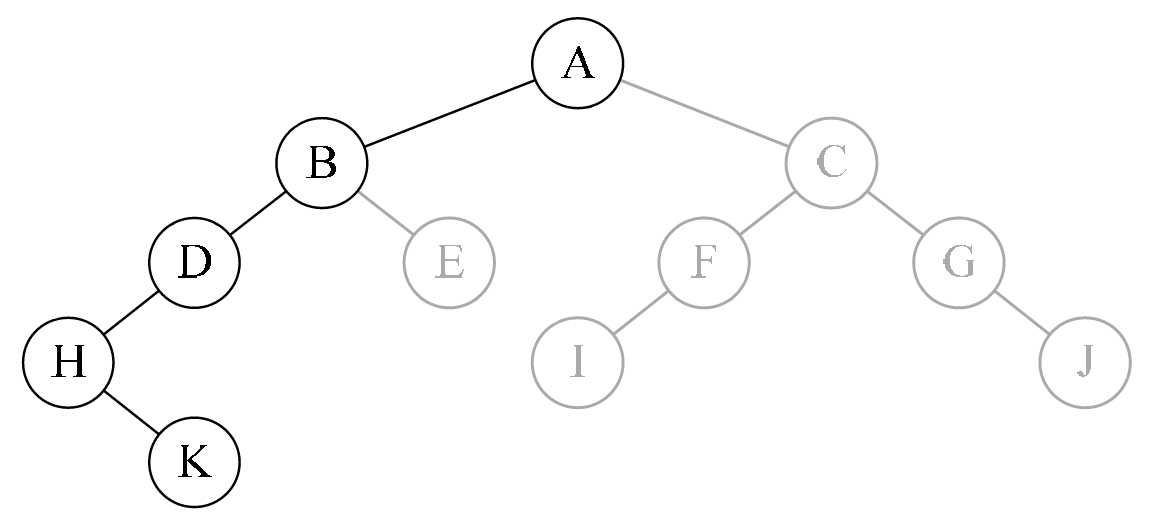
    image.pngimage.png
    再次递归调用PreOrderTraverse(T->lchild);访问了K结点的左孩子，K结点无左孩子，返回，调用PreOrderTra-verse(T->rchild);访问了K结点的右孩子，也是null，返回。于是此函数执行完毕，
    返回到上一级递归的函数（即打印H结点时的函数），也执行完毕，
    返回到打印结点D时的函数，调用PreOrderTraverse(T->rchild);访问了D结点的右孩子，不存在，
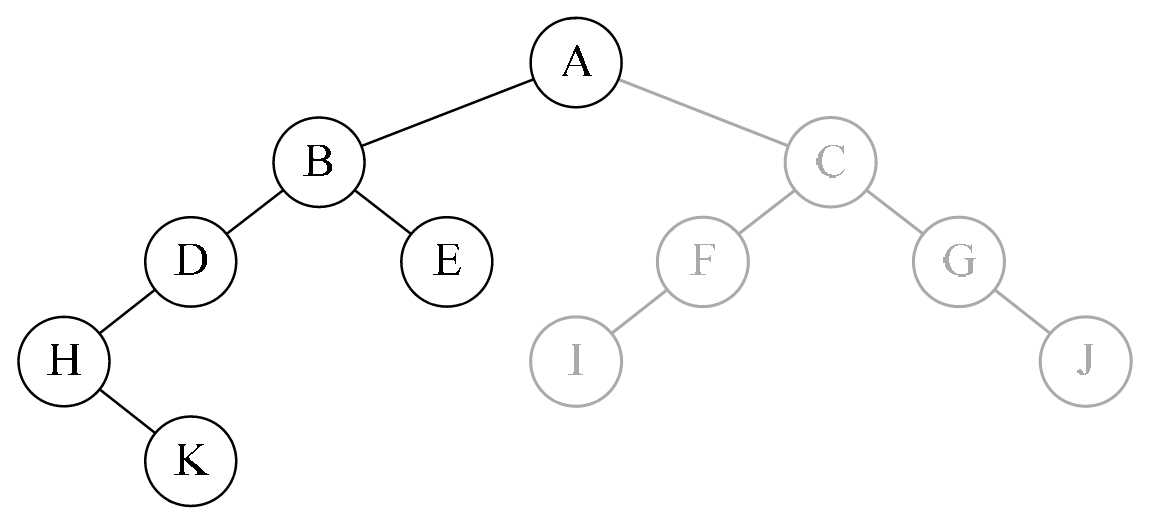
    返回到B结点，调用PreOrderTra-verse(T->rchild);找到了结点E，打印字母E，

    image.png
    由于结点E没有左右孩子，返回打印结点B时的递归函数，递归执行完毕，
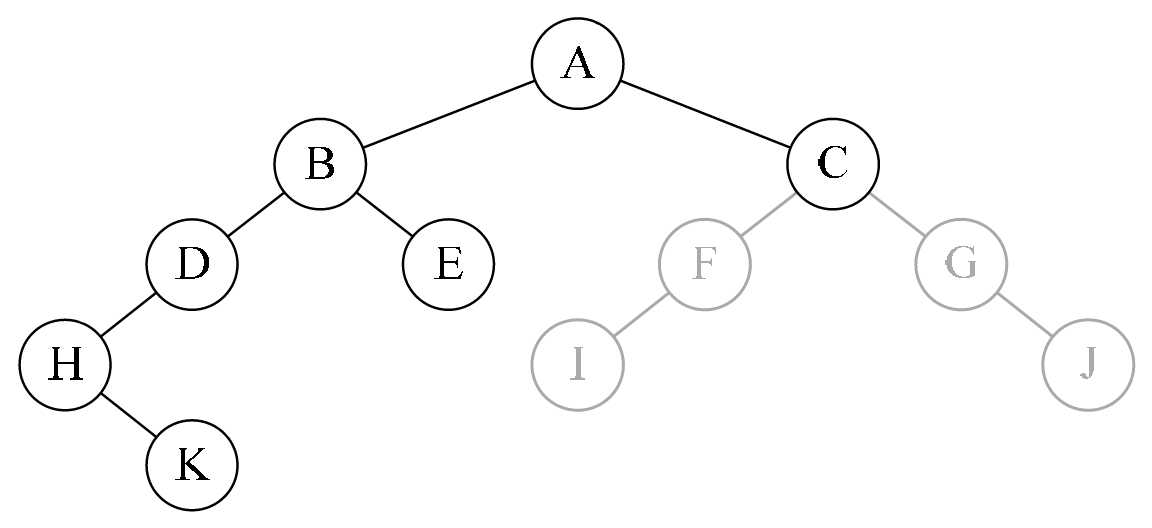
    返回到最初的PreOrderTraverse，调用PreOrderTra-verse(T->rchild);访问结点A的右孩子，打印字母C，

    中序遍历：HKDBEAIFCGJ

    1. /* 二叉树的中序遍历递归算法 */
    2. void InOrderTraverse(BiTree T)
    3. {
    4.     if (T == NULL)
    5.         return;
    7.     /* 中序遍历左子树 */
    8.     InOrderTraverse(T->lchild);    
    10.     /* 显示结点数据，可以更改为其他对结点操作 */
    11.     printf("%c", T->data);         
    13.     /* 最后中序遍历右子树 */
    14.     InOrderTraverse(T->rchild);    
    15. }

    那么二叉树的中序遍历算法是如何呢？
    它和前序遍历算法仅仅只是代码的顺序上的差异。
    换句话说，它等于是把调用左孩子的递归函数提前了。

    后序遍历：

    1. /* 二叉树的后序遍历递归算法 */
    2. void PostOrderTraverse(BiTree T)
    3. {
    4.     if (T == NULL)
    5.         return;
    7.     /* 先后序遍历左子树 */
    8.     PostOrderTraverse(T->lchild);    
    10.     /* 再后序遍历右子树 */
    11.     PostOrderTraverse(T->rchild);    
    13.     /* 显示结点数据，可以更改为其他对结点操作 */
    14.     printf("%c", T->data);           
    15. }

    层序遍历：（Z字遍历）