我们把平时所用的标准四则运算表达式，即“9+(3-1)×3+10÷2”叫做中缀表达式。因为所有的运算符号都在两数字的中间，现在我们的问题就是中缀到后缀的转化。

    中缀表达式“9+(3-1)×3+10÷2”转化为后缀表达式“9 3 1-3*+10 2/+”。
    规则：
    从左到右遍历中缀表达式的每个数字和符号，

    • 若是数字就输出，即成为后缀表达式的一部分；
    • 若是符号，则判断其与栈顶符号的优先级，
      • 是右括号或优先级低于等于栈顶符号（乘除优先加减）则栈顶元素依次出栈并输出，并将当前符号进栈，一直到最终输出后缀表达式为止。

    1．初始化一空栈，用来对符号进出栈使用。如图4-9-6的左图所示。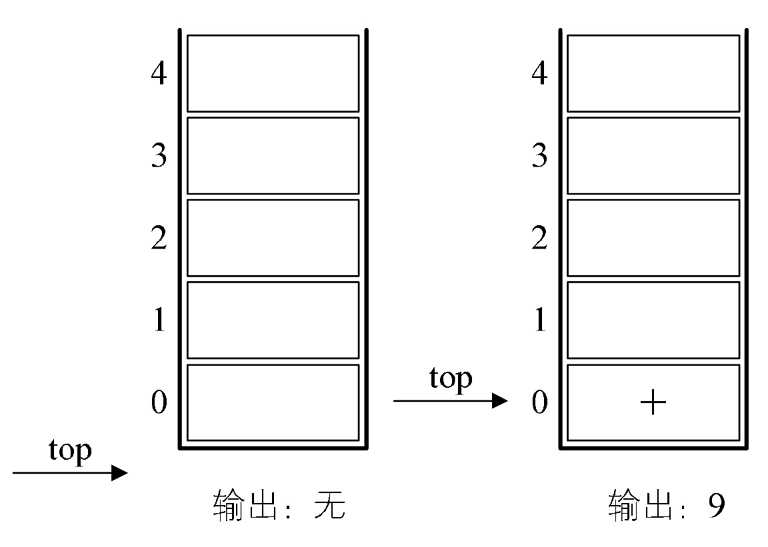
    image.png
    图4-9-6
    “9+(3-1)×3+10÷2”
    2．第一个字符是数字9，输出9，后面是符号“+”，进栈。如图4-9-6的右图所示。
    3．第三个字符是“(”，依然是符号，因其只是左括号，还未配对，故进栈。如图4-9-7的左图所示。
    4．第四个字符是数字3，输出，总表达式为93，接着是“-”，进栈。如图4-9-7的右图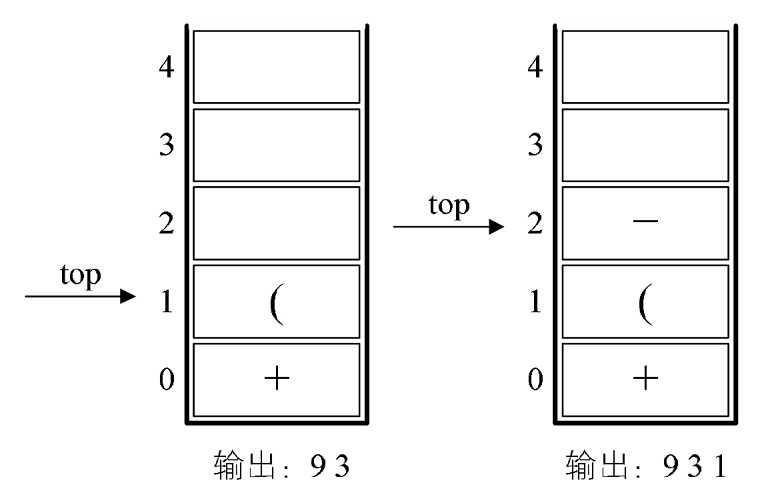
    image.png
    图4-9-7
    “9+(3-1)×3+10÷2”
    5．接下来是数字1，输出，总表达式为 9 31，后面是符号“)”，此时，我们需要去匹配此前的“(”，所以栈顶依次出栈，并输出，直到“(”出栈为止。此时左括号上方只有“-”，因此输出“-”。总的输出表达式为 9 3 1-。如图4-9-8的左图所示。
    6．紧接着是符号“×”，因为此时的栈底符号为“+”号，优先级低于“×”，因此不输出，“”进栈。接着是数字3，输出，总的表达式为 9 3 1-3。如图4-9-8的右图所示。
    “9+(3-1)×3+10÷2”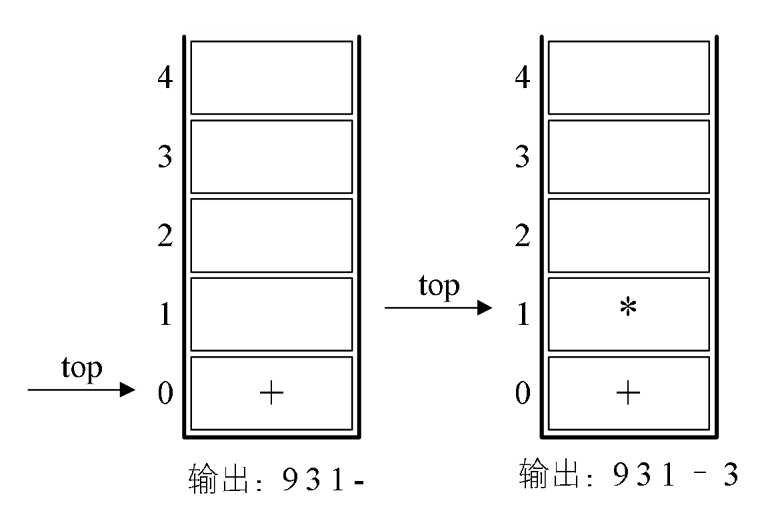
    image.png
    图4-9-8
    “9+(3-1)×3+10÷2”
    7．之后是符号“+”，此时当前栈顶元素“ ”比这个“+”的优先级高，因此栈中元素出栈并输出（没有比“+”号更低的优先级，所以全部出栈），总输出表达式为9 3 1-3 +。然后将当前这个符号“+”进栈。也就是说，前6张图的栈底的“+”是指中缀表达式中开头的9后面那个“+”，而图4-9-9左图中的栈底（也是栈顶）的“+”是指“9+(3-1)×3+”中的最后一个“+”。
    8．紧接着数字10，输出，总表达式变为9 31-3    +10。后是符号“÷”，所以“/”进栈。如图4-9-9的右图所示。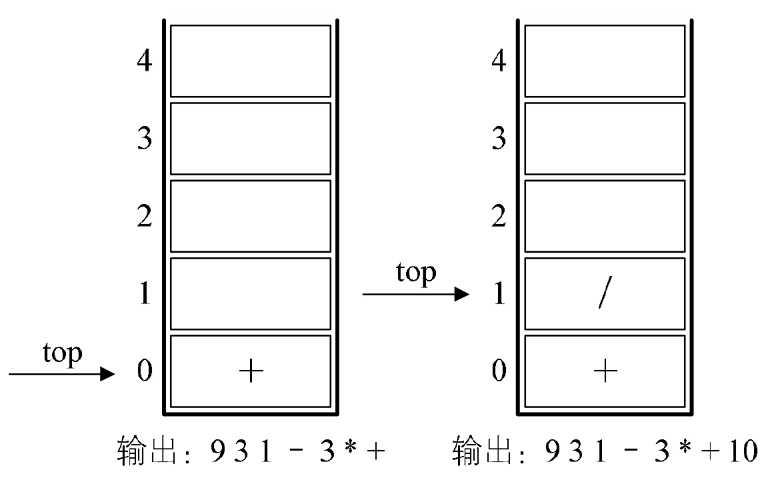
    image.png
    图4-9-9
    9．最后一个数字2，输出，总的表达式为9 3 1 - 3 * + 10 2。如图4-9-10的左图所示。
    10．因已经到最后，所以将栈中符号全部出栈并输出。最终输出的后缀表达式结果为93 1-3 +10 2/+。如图4-9-10的右图所示。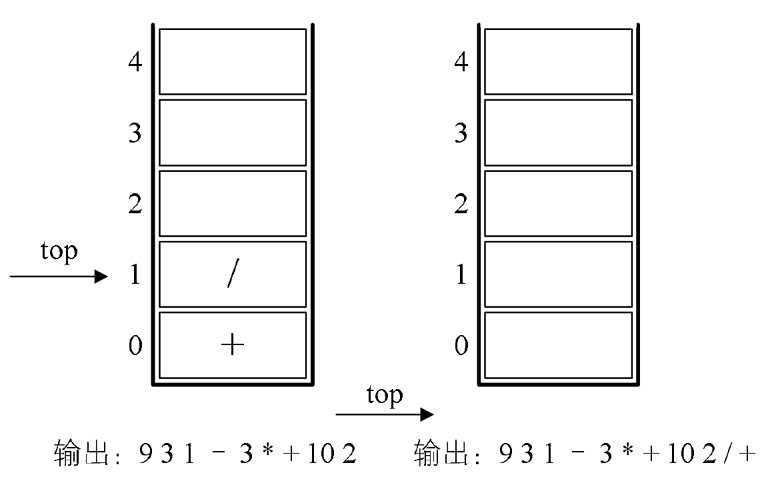
    image.png
    图4-9-10
    从刚才的推导中你会发现，要想让计算机具有处理我们通常的标准（中缀）表达式的能力，最重要的就是两步：

    • 将中缀表达式转化为后缀表达式（栈用来进出运算的符号）。
    • 将后缀表达式进行运算得出结果（栈用来进出运算的数字）。

    整个过程，都充分利用了栈的后进先出特性来处理，理解好它其实也就理解好了栈这个数据结构。
    好了，休息一下，一会儿我们继续，接下来会讲队列。