[

](https://www.zhihu.com/search?type=content&q=%E4%B8%AD%E7%BC%80%E8%A1%A8%E8%BE%BE%E5%BC%8F%E8%BD%AC%E5%90%8E%E7%BC%80%E8%A1%A8%E8%BE%BE%E5%BC%8F)
优先级:https://zhuanlan.zhihu.com/p/422390012
中缀表达式中，优先级：{ (, ) } > { *, / } > { +, - }
注意，同级运算中，先出现的（左侧）优先级高。
后缀表达式中，先出现的运算符优先与操作数结合。即，优先级：{ 靠前 } > { 靠后 }

换元法:https://zhuanlan.zhihu.com/p/135433833
在表达式求值的过程中，常用到将中缀表达式转化为后缀表达式或前缀表达式的过程
我们常见的表达式形式为中缀表达式，对于简单的中缀表达式可以很容易转化为前缀表达式或后缀表达式
例如,中缀表达式a+b，其前缀表达式为+ab,后缀表达式为ab+
较复杂的表达式则不易直接得出结果，这里我们将通过栈来实现相应的转化
示例表达式：[(A+B)*C]-[E-F]
转化为前缀表达式：

  1. 先计算A+B，转化为+AB
  2. +AB作为整体与C运算，转化为*+ABC
  3. 运算E-F，转化为-EF
  4. 将+ABC与E-F都作为整体执行-运算，转化为**-+ABC-EF**

转化为后缀表达式：

  1. 先计算A+B，转化为AB+
  2. AB+作为整体与C运算，转化为AB+C*
  3. 运算E-F，转化为EF-
  4. 将AB+C与EF-作为整体执行-运算，转化为**AB+CEF—**

    算法思想

    如果检测到数字，则直接加入到后缀表达式中
    如果检测到运算符时：
  1. 若为‘（’，入栈
  2. 若为‘）’，则依次将栈中的运算符加入后缀表达式，直到出现‘（’，并从栈中删除‘（’
  3. 若为‘+’，‘-’，‘*’，‘/’
  • 栈空，入栈
  • 栈顶元素为‘（’,入栈
  • 高于栈顶元素优先级，入栈
  • 否则，依次弹出栈顶运算符，直到一个优先级比它低的运算符或‘（’为止

遍历完成，若栈非空，依次弹出栈中所有元素
该算法使得栈顶运算符处于较高优先级，并先弹出栈，进入后缀表达式

过程分析

示例：（（A+B）C）-（E-F）
1.连续两个’（’，入栈
（当前后缀表达式： ）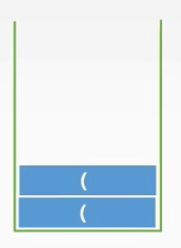
image.png
前缀表达式遍历进度（（
2.遍历到数字A，加入到后缀表达式
（当前后缀表达式：A）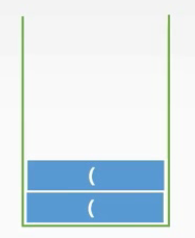
image.png
前缀表达式遍历进度（（A
3.遍历到运算符+，由于栈顶元素为‘（’，直接入栈。
(当前后缀表达式：A)
4.接着遍历数字B，加入到后缀表达式
(当前后缀表达式：AB)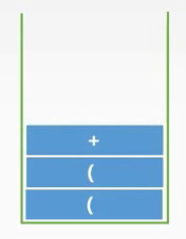
image.png
前缀表达式遍历进度（（A+B
5.遍历‘）’，依次将栈中的运算符加入后缀表达式，直到出现‘（’,并删除栈顶的‘（’
(当前后缀表达式：AB+)
注：括号是不会出现在后缀表达式或前缀表达式中的
image.png
前缀表达式遍历进度（（A+B）
6.遍历到，栈顶为‘（’，直接入栈
7.接着遍历数字C，直接加入到后缀表达式中
(当前后缀表达式：AB+C)
image.png
前缀表达式遍历进度（（A+B）C
8.继续遍历到‘）’，依次将栈中的运算符加入后缀表达式，直到出现‘（’,并删除栈顶的‘（’
【当前后缀表达式：AB+C】
image.png
前缀表达式遍历进度（（A+B）C）
9.接着遍历到-，栈空，入栈
【当前后缀表达式：AB+C】
image.png
前缀表达式遍历进度（（A+B）C）-
10.遍历‘（’，直接入栈
【当前后缀表达式：AB+C】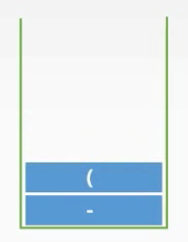
image.png
前缀表达式遍历进度（（A+B）C）-（
11.遍历到数字E,直接加入到后缀表达式
【当前后缀表达式：AB+CE】
12.遍历到-，栈顶元素为‘（’，入栈
【当前后缀表达式：AB+CE】
13.遍历到F，加入到后缀表达式
【当前后缀表达式：AB+CEF】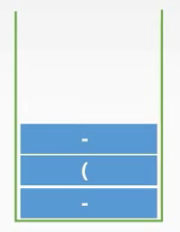
image.png
前缀表达式遍历进度（（A+B）C）-（E-F
14.遍历到‘）’，依次将栈中的运算符加入后缀表达式，直到出现‘（’,并删除栈顶的‘（’
【当前后缀表达式：AB+CEF-】
image.png
前缀表达式遍历进度（（A+B）C）-（E-F）遍历完毕
15.遍历完毕，栈非空，将栈中元素依次弹出
【当前后缀表达式：AB+CEF—】
image.png
成功得到后缀表达式！！！

代码实现

  1. #include<stdio.h>
  3. #define ElemType char
  4. #define MaxSize 50
  6. typedef struct {
  7.     ElemType data[MaxSize];
  8.     int top;
  9. }SqStack;
  11. void initStack(SqStack& S)
  12. {
  13.     S.top = -1;   //初始化栈顶指针
  14. }
  16. bool StackEmpty(SqStack S)
  17. {
  18.     if (S.top == -1)   //栈空
  19.         return true;
  20.     else
  21.         return false;  //栈不空
  22. }
  24. bool Push(SqStack& S, ElemType x)
  25. {
  26.     if (S.top == MaxSize - 1)      //栈满 不能执行入栈操作
  27.         return false;
  28.     S.top++;                      //指针先加1，再入栈
  29.     S.data[S.top] = x;
  30.     return true;
  31. }
  33. bool Pop(SqStack& S, ElemType& x)
  34. {
  35.     if (S.top == -1)              //栈空 不能执行出栈操作
  36.         return false;
  37.     x = S.data[S.top];            //先出栈 指针再减1
  38.     S.top--;
  39.     return true;
  40. }
  42. bool GetPop(SqStack S, ElemType& x)
  43. {
  44.     if (S.top == -1)            //栈空报错
  45.         return false;
  46.     x = S.data[S.top];          //用x存储栈顶元素
  47.     return true;
  48. }
  50. int main()
  51. {
  52.     SqStack S;
  53.     initStack(S);
  55.     char NifixExpression[] = { '(','(','A','+','B',')','*','C',')','-','(','E','-','F',')','\0' };
  56.     char PostfixExpression[60];    //在字符数组最后添加'\0',作为结束标志
  57.     int index = 0;
  58.     char* p = NifixExpression;
  59.     while (*p!='\0')
  60.     {
  61.         if (*p == '(')         //如果为左括号，直接入栈
  62.         {
  63.             Push(S, *p);
  64.             p++;
  65.         }
  66.         else if (*p == ')')//若为右括号，依次弹出栈中运算符，直到'(',并删除'('--用出栈不保存数据实现
  67.         {
  68.             while (S.data[S.top] != '(')
  69.             {
  70.                 char temp;
  71.                 Pop(S, temp);
  72.                 if (temp == '+' || temp == '-' || temp == '*' || temp == '/')
  73.                 {
  74.                     PostfixExpression[index] = temp;
  75.                     index++;
  76.                 }
  77.             }
  78.             char temp;
  79.             Pop(S, temp);     //把左括号也出栈
  80.             p++;
  81.         }
  82.         else if (*p >= 'A' && *p <= 'Z') //这里用大写字母代替表达式中的数字，为大写字母则直接进入后缀表达式
  83.         {
  84.             PostfixExpression[index] = *p;
  85.             index++;
  86.             p++;
  87.         }
  88.         else
  89.         {
  90.             if (*p == '+' || *p == '-')
  91.             {
  92.                 if (S.data[S.top] == '('||StackEmpty)//如果遍历到'+''-',且栈为空或栈顶为'(',直接入栈
  93.                 {
  94.                     Push(S, *p);
  95.                     p++;
  96.                 }
  97.                 else {
  98.                     while (S.data[S.top] != '('&&!StackEmpty)//依次弹出较高优先级运算符，直到'('
  99.                     {
  100.                         char temp;
  101.                         Pop(S, temp);
  102.                         PostfixExpression[index] = temp;
  103.                         index++;
  104.                     }
  105.                 }
  106.             }
  107.             else
  108.             {
  109.                 Push(S, *p);
  110.                 p++;
  111.             }
  112.         }
  113.     }
  114.     if (!StackEmpty(S))          //若栈不为空，依次弹出其中的运算符
  115.     {
  116.         while (S.top != -1)
  117.         {
  118.             char temp;
  119.             Pop(S,temp);
  120.             PostfixExpression[index] = temp;
  121.             index++;
  122.         }
  123.     }
  124.     PostfixExpression[index] = '\0';         //在字符数组后加'\0',作为结束标志
  125.     printf("中缀表达式为：%s",NifixExpression);
  126.     printf("\n");
  127.     printf("后缀表达式为：%s", PostfixExpression);
  130. }