为了解释后缀表达式的好处，我们先来看看，计算机如何应用后缀表达式计算出最终的结果20的。
    后缀表达式：9 3 1-3+10 2/+
    规则：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果。
    1．初始化一个空栈。此栈用来对要运算的数字进出使用。如图4-9-1的左图所示。
    2．后缀表达式中前三个都是数字，所以9、3、1进栈，如图4-9-1的右图所示。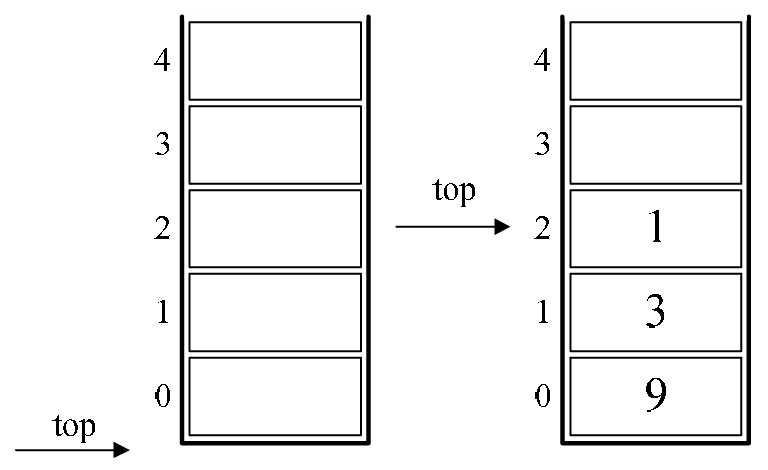
    image.png
    图4-9-1
    后缀表达式：9 3 1-3    +10 2/+
    3．接下来是“-”，所以将栈中的1出栈作为减数，3出栈作为被减数，并运算3-1得到2，再将2进栈，如图4-9-2的左图所示。
    4．接着是数字3进栈，如图4-9-2的右图所示。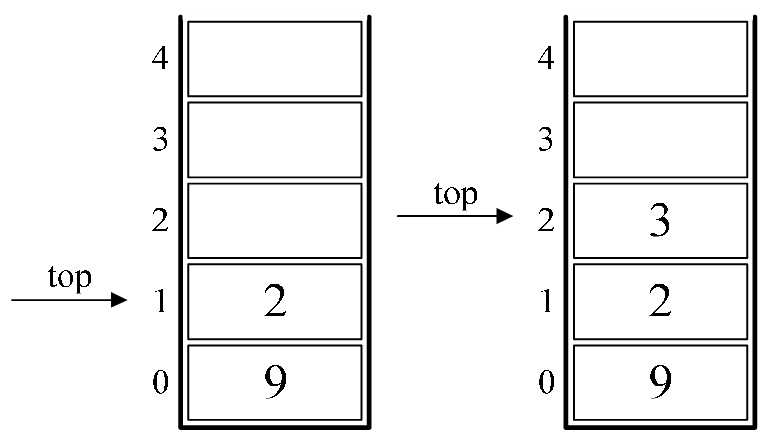
    image.png
    图4-9-2
    后缀表达式：9 3 1-3+10 2/+
    5．后面是“    ”，也就意味着栈中3和2出栈，2与3相乘，得到6，并将6进栈，如图4-9-3的左图所示。
    6．下面是“+”，所以栈中6和9出栈，9与6相加，得到15，将15进栈，如图4-9-3的右图所示。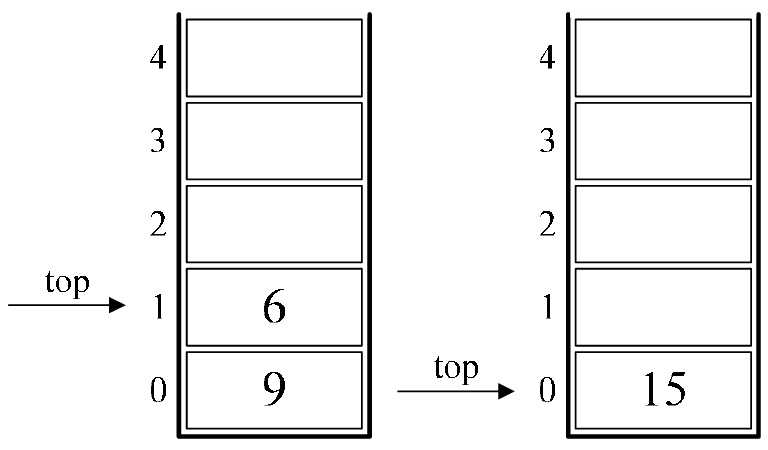
    image.png
    图4-9-3
    后缀表达式：9 3 1-3*+10 2/+
    7．接着是10与2两数字进栈，如图4-9-4的左图所示。
    8．接下来是符号“/”，因此，栈顶的2与10出栈，10与2相除，得到5，将5进栈，如图4-9-4的右图所示。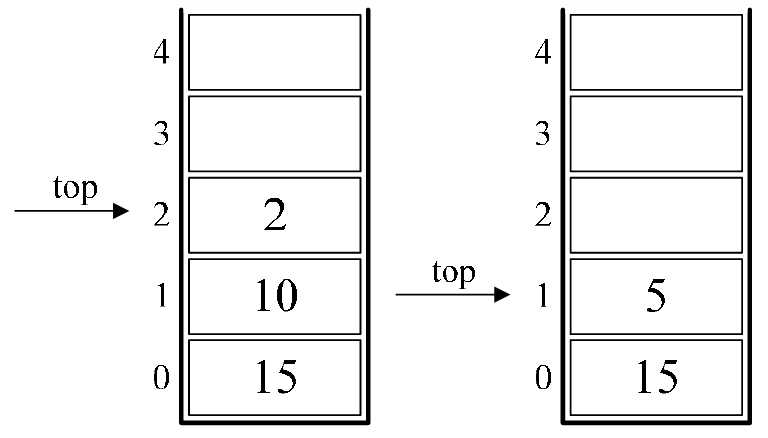
    image.png
    图4-9-4
    9．最后一个是符号“+”，所以15与5出栈并相加，得到20，将20进栈，如图4-9-5的左图所示。10．结果是20出栈，栈变为空，如图4-9-5的右图所示。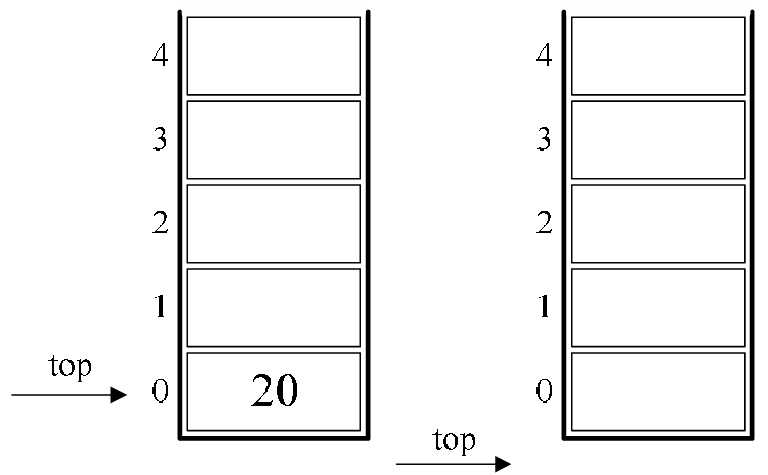
    image.png
    图4-9-5
    果然，后缀表达法可以很顺利解决计算的问题。现在除了睡觉的同学，应该都有同样的疑问，就是这个后缀表达式“9 3 1-3 +10 2/+”是怎么出来的？这个问题不搞清楚，等于没有解决。所以下面，我们就来推导如何让“9+(3-1)×3+10÷2”转化为“9 3 1-3 +10 2/+”。