刚才我们分别从双亲的角度和从孩子的角度研究树的存储结构，
    如果我们从树结点的兄弟的角度考虑又会如何呢？
    当然，对于树这样的层级结构来说，只研究结点的兄弟是不行的，我们观察后发现，任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。
    因此，我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟。
    结点结构如表6-4-9所示。
    表6-4-9
    data firstchild rightsib

    其中data是数据域，
    firstchild为指针域，存储该结点的第一个孩子结点的存储地址，
    right-sib是指针域，存储该结点的右兄弟结点的存储地址。
    结构定义代码如下。

    1. /* 树的孩子兄弟表示法结构定义 */
    2. typedef struct CSNode
    3. {
    4.     TElemType data;
    5.     struct CSNode *firstchild, 
    6.     *rightsib;
    7. } CSNode, *CSTree;

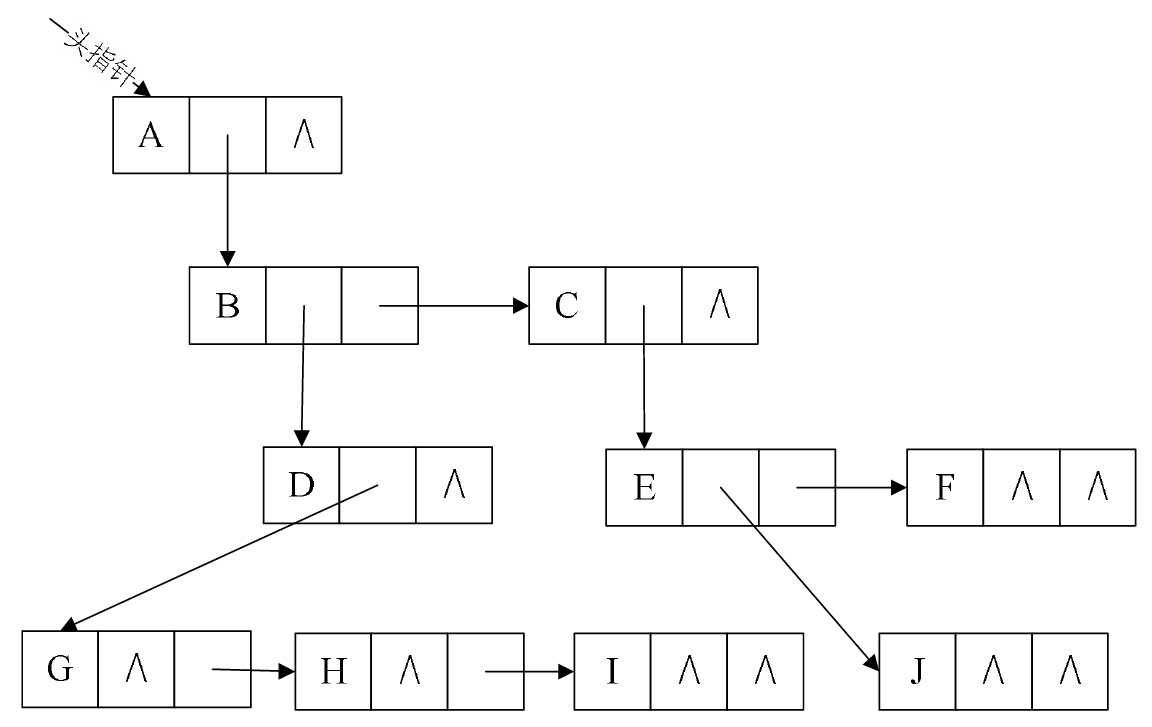
    image.png对于图6-4-1的树来说，这种方法实现的示意图如图6-4-6所示。
    image.png
    图6-4-6
    这种表示法，

    • 给查找某个结点的某个孩子带来了方便，只需要通过fistchild找到此结点的长子，然后再通过长子结点的rightsib找到它的二弟，接着一直下去，直到找到具体的孩子。

    当然，如果想找某个结点的双亲，这个表示法也是有缺陷的，那怎么办呢？
    呵呵，对，如果真的有必要，完全可以再增加一个parent指针域来解决快速查找双亲的问题，这里就不再细谈了。

    • 其实这个表示法的最大好处是它把一棵复杂的树变成了一棵二叉树。

    如何变形：
    如果有1个孩子，正常处理，一下一右
    如果有2个及以上的孩子，
    左孩子一下再右串其兄弟
    兄弟一右
    我们把图6-4-6变变形就成了图6-4-7这个样子。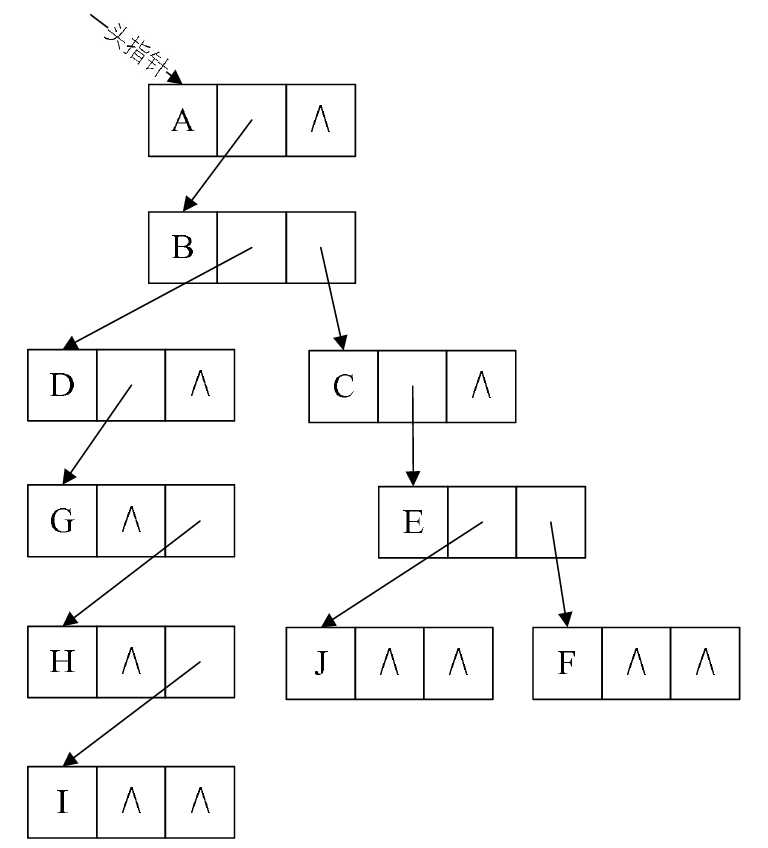
    image.png
    图6-4-7

    这样就可以充分利用二叉树的特性和算法来处理这棵树了。嗯？有人问，二叉树是什么？哈哈，别急，这正是我接下来要重点讲的内容。