广度优先遍历（Breadth_First_Search），又称为广度优先搜索，简称BFS。

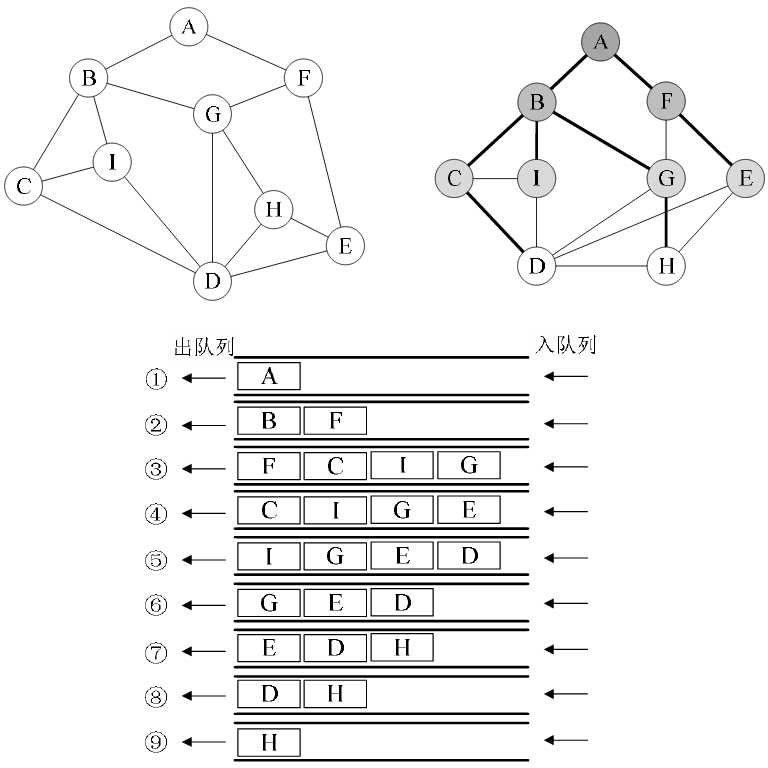
    image.png
    图7-5-3

    如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历了。
    我们将图7-5-3的第一幅图稍微变形，变形原则是顶点A放置在最上第一层，让与它有边的顶点B、F为第二层，再让与B和F有边的顶点C、I、G、E为第三层，再将这四个顶点有边的D、H放在第四层，
    如图7-5-3的第二幅图所示。此时在视觉上感觉图的形状发生了变化，其实顶点和边的关系还是完全相同的。

    1. //以下是邻接矩阵结构的广度优先遍历算法。
    3. /* 邻接矩阵的广度遍历算法 */
    4. void BFSTraverse(MGraph G)
    5. {
    6.     int i, j;
    8.     Queue Q;
    10.     for (i = 0; i < G.numVertexes; i++)
    11.         visited[i] = FALSE;
    13.     /* 初始化一辅助用的队列 */
    14.     InitQueue(&Q);                                   
    16.     /* 对每一个顶点做循环 */
    17.     for (i = 0; i < G.numVertexes; i++)              
    18.     {
    19.         /* 若是未访问过就处理 */
    20.         if (!visited[i])                             
    21.         {
    22.             /* 设置当前顶点访问过 */
    23.             visited[i]=TRUE;                         
    25.             /* 打印顶点，也可以其他操作 */
    26.             printf("%c ", G.vexs[i]);                
    28.             /* 将此顶点入队列 */
    29.             EnQueue(&Q,i);                           
    31.             /* 若当前队列不为空 */
    32.             while (!QueueEmpty(Q))                   
    33.             {
    34.                 /* 将队中元素出队列，赋值给i */
    35.                 DeQueue(&Q, &i);                     
    37.                 for (j = 0; j < G.numVertexes; j++)
    38.                 {
    39.                     /* 判断其他顶点若与当前顶点存在边且未访问过 */
    40.                     if (G.arc[i][j] == 1 && !visited[j])
    41.                     {
    42.                         /* 将找到的此顶点标记为已访问 */
    43.                         visited[j]=TRUE;             
    45.                         /* 打印顶点 */
    46.                         printf("%c ", G.vexs[j]);    
    48.                         /* 将找到的此顶点入队列 */
    49.                         EnQueue(&Q,j);               
    50.                     }
    52.                 }
    54.             }
    56.         }
    58.     }
    60. }
    1. //对于邻接表的广度优先遍历，代码与邻接矩阵差异不大，代码如下。
    3. /* 邻接表的广度遍历算法 */
    4. void BFSTraverse(GraphAdjList GL)
    5. {
    6.     int i;
    8.     EdgeNode *p;
    10.     Queue Q;
    12.     for (i = 0; i < GL->numVertexes; i++)
    13.         visited[i] = FALSE;
    15.     InitQueue(&Q);
    17.     for (i = 0; i < GL->numVertexes; i++)
    18.     {
    19.         if (!visited[i])
    20.         {
    21.             visited[i] = TRUE;
    23.             /* 打印顶点，也可以其他操作 */
    24.             printf("%c ", GL->adjList[i].data);    
    26.             EnQueue(&Q, i);
    28.             while (!QueueEmpty(Q))
    29.             {
    30.                 DeQueue(&Q, &i);
    32.                 /* 找到当前顶点边表链表头指针 */
    33.                 p = GL->adjList[i].firstedge;      
    35.                 while (p)
    36.                 {
    37.                     /* 若此顶点未被访问 */
    38.                     if (!visited[p->adjvex])       
    39.                     {
    40.                         visited[p->adjvex] = TRUE;
    42.                         printf("%c ", GL->adjList[p->adjvex].data);
    44.                         /* 将此顶点入队列 */
    45.                         EnQueue(&Q, p->adjvex);    
    46.                     }
    47.                     /* 指针指向下一个邻接点 */
    48.                     p = p->next;                   
    49.                 }
    51.             }
    53.         }
    55.     }
    57. }

    对比图的深度优先遍历与广度优先遍历算法，
    你会发现，它们在

    • 时间复杂度上是一样的，不同之处仅仅在于对顶点访问的顺序不同。
    • 空间复杂度相同，都是O(n)[借助了堆栈or队列]。

    可见两者在全图遍历上是没有优劣之分的，只是视不同的情况选择不同的算法。

    不过如果图顶点和边非常多，不能在短时间内遍历完成，遍历的目的是为了寻找合适的顶点，那么选择哪种遍历就要仔细斟酌了。

    • 深度优先更适合目标比较明确，以找到目标为主要目的的情况，
    • 广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。

    这里还要再多说几句，对于深度和广度而言，已经不是简单的算法实现问题，完全可以上升到方法论的角度。
    你求学是博览群书、不求甚解，还是深钻细研、鞭辟入里；
    你旅游是走马观花、蜻蜓点水，还是下马看花、深度体验；
    你交友是四海之内皆兄弟，还是人生得一知己足矣……其实都无对错之分，只视不同人的理解而有了不同的诠释。
    我个人觉得深度和广度是既矛盾又统一的两个方面，偏颇都不可取，还望大家自己慢慢体会。