特殊二叉树

1．斜树
顾名思义，斜树一定要是斜的，但是往哪斜还是有讲究。

• 所有的结点都只有左子树的二叉树叫左斜树。
• 所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

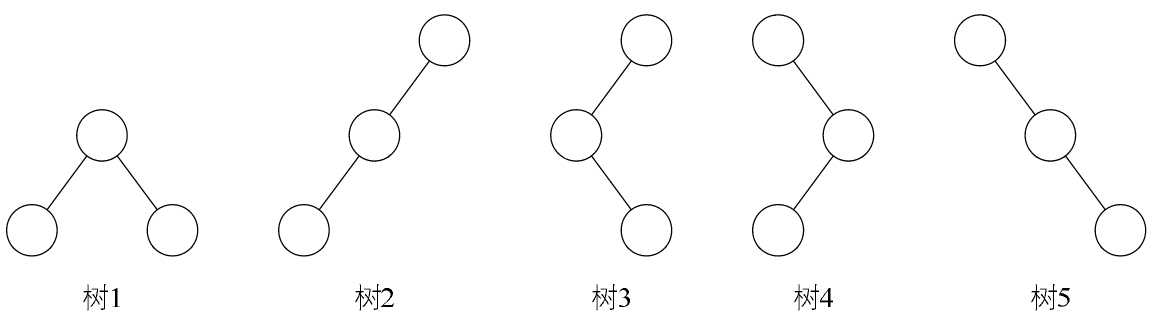
图6-5-4
图6-5-4中的树2就是左斜树，树5就是右斜树。

斜树有很明显的特点，

• 就是每一层都只有一个结点，
• 结点的个数与二叉树的深度相同。

有人会想，这也能叫树呀，与我们的线性表结构不是一样吗。
对的，其实线性表结构就可以理解为是树的一种极其特殊的表现形式。

以下两种特殊的二叉树

• 满二叉树
• 完全二叉树

为什么要研究这两种特殊的二叉树：
因为它们在顺序存储方式下可以复原！

2．满二叉树
苏东坡曾有词云：“人有悲欢离合，月有阴晴圆缺，此事古难全”。
意思就是完美是理想，不完美才是人生。
我们通常举的例子也都是左高右低、参差不齐的二叉树。那是否存在完美的二叉树呢？
嗯，有同学已经在空中手指比划起来。对的，完美的二叉树是存在的。

在一棵二叉树中，

• 如果所有分支结点都存在左子树和右子树，
• 并且所有叶子都在同一层上，

这样的二叉树称为满二叉树。

图6-5-5就是一棵满二叉树，从样子上看就感觉它很完美。

图6-5-5
单是每个结点都存在左右子树，不能算是满二叉树，
还必须要所有的叶子都在同一层上，这就做到了整棵树的平衡。
因此，满二叉树的特点有：
（1）叶子只能出现在最下一层。出现在其他层就不可能达成平衡。
（2）非叶子结点的度一定是2。否则就是“缺胳膊少腿”了。
（3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

3．完全二叉树：编号连续不打断左连续，所以不要右撇子
对一棵具有n个结点的二叉树按层序编号，
如果编号为i（1≤i≤n）的结点 与 同样深度的满二叉树中编号为i的结点
在二叉树中位置完全相同，则这棵二叉树称为完全二叉树，如图6-5-6所示。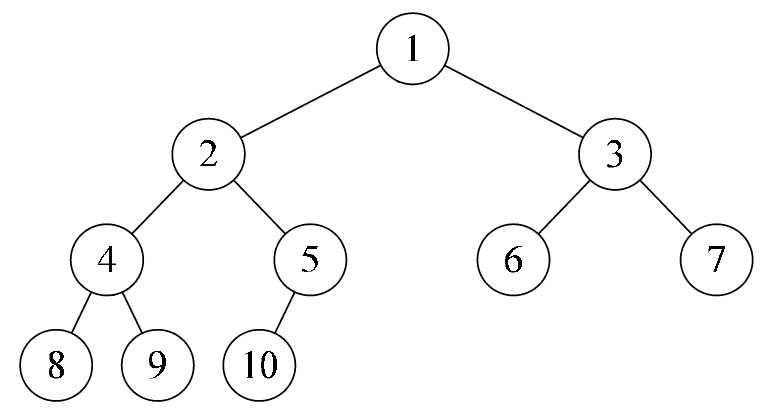

图6-5-6
这是一种有些理解难度的特殊二叉树。
首先从字面上要区分，“完全”和“满”的差异，

• 满二叉树一定是一棵完全二叉树，
• 但完全二叉树不一定是满的。

其次，完全二叉树的所有结点与同样深度的满二叉树，它们按层序编号相同的结点，是一一对应的。
这里有个关键词是按层序编号，

• 像图6-5-7中的树1，因为5结点没有左子树，却有右子树，那就使得按层序编号的第10个编号空档了。
• 同样道理，图6-5-7中的树2，由于3结点没有子树，所以使得6、7编号的位置空档了。
• 图6-5-7中的树3又是因为5编号下没有子树造成第10和第11位置空档。
• 只有图6-5-6中的树，尽管它不是满二叉树，但是编号是连续的，所以它是完全二叉树。

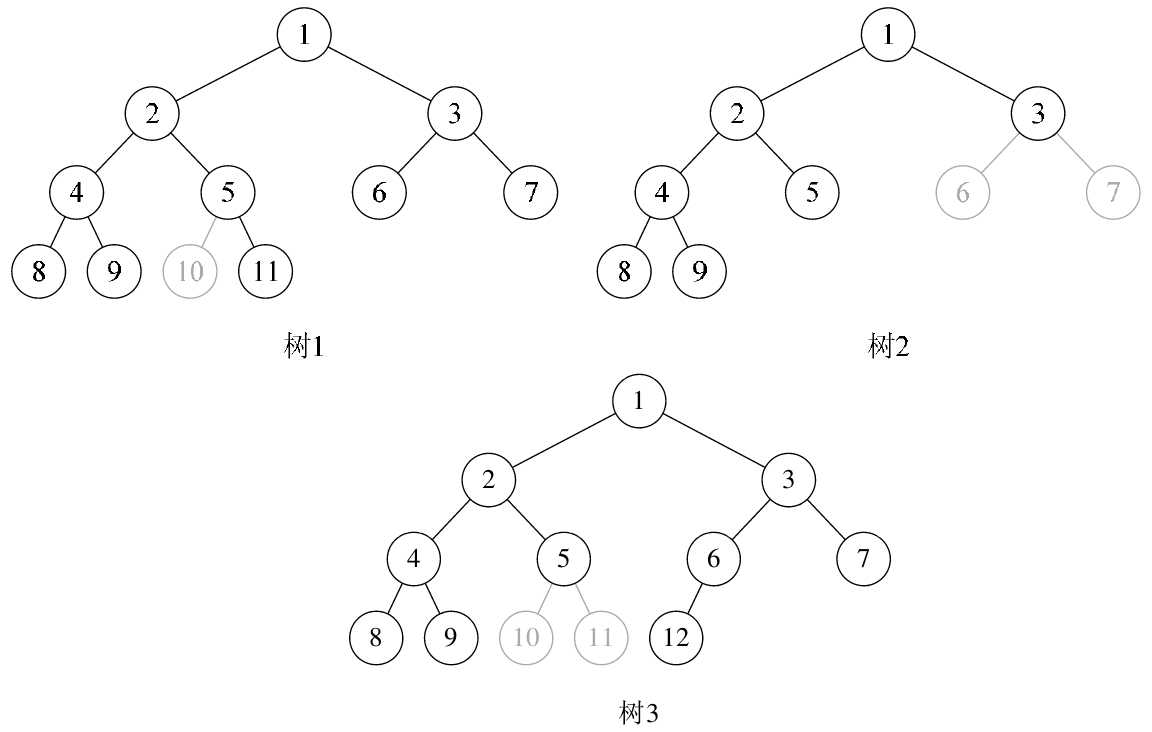
图6-5-7

从这里我也可以得出一些完全二叉树的特点：
（1）叶子结点只能出现在最下两层。
（2）最下层的叶子一定集中在左部连续位置。
（3）倒数二层，若有叶子结点，一定都在右部连续位置。
（4）如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。
（5）同样结点数的二叉树，完全二叉树的深度最小。

从上面的例子，也给了我们一个判断某二叉树是否是完全二叉树的办法，那就是看着树的示意图，心中默默给每个结点按照满二叉树的结构逐层顺序编号，如果编号出现空档，就说明不是完全二叉树，否则就是。

完全二叉树可以包含斜树和满二叉树