既然栈是线性表的特例，那么栈的顺序存储其实也是线性表顺序存储的简化，我们简称为顺序栈。
    线性表是用数组来实现的，想想看，对于栈这种只能一头插入删除的线性表来说，用数组哪一端来作为栈顶和栈底比较好？
    对，没错，下标为0的一端作为栈底比较好，因为首元素都存在栈底，变化最小，所以让它作栈底。栈顶是表尾尾插尾删方便操作。

    我们定义一个top变量来指示栈顶元素在数组中的位置，
    这top就如同中学物理学过的游标卡尺的游标，如图4-4-1，它可以来回移动，意味着栈顶的top可以变大变小，但无论如何游标不能超出尺的长度。同理，若存储栈的长度为StackSize，则栈顶位置top必须小于StackSize。

    当栈存在一个元素时，top等于0，因此通常把空栈的判定条件定为top等于-1。
    image.png
    图4-4-1

    来看栈的结构定义

    1. /* SElemType类型根据实际情况而定，这里假设为int */
    2. typedef int SElemType;    
    3. typedef struct
    4. {
    5.     SElemType data[MAXSIZE];
    6.     /* 用于栈顶指针 */
    7.     int top;              
    8. }SqStack;


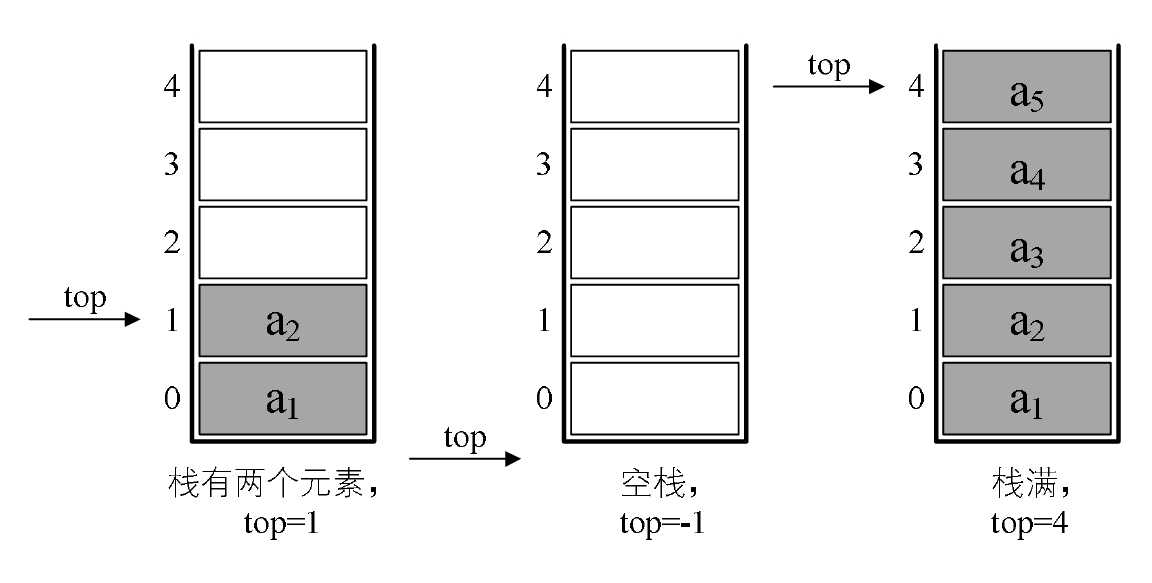
    若现在有一个栈，StackSize是5，
    则栈普通情况、空栈和栈满的情况、空栈和栈满的情况示意图如图所示。
    image.png