我们假设一个队列有n个元素，则顺序存储的队列需建立一个大于n的数组，并把队列的所有元素存储在数组的前n个单元，数组下标为0的一端即是队头。
    所谓的入队列操作，其实就是在队尾追加一个元素，不需要移动任何元素，因此时间复杂度为O(1)，如图4-12-1所示。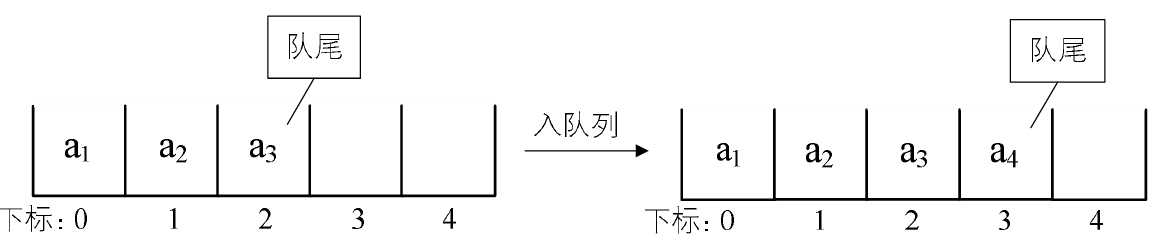
    image.png
    图4-12-1
    与栈不同的是，队列元素的出列是在队头，即下标为0的位置，那也就意味着，队列中的所有元素都得向前移动，以保证队列的队头，也就是下标为0的位置不为空，此时时间复杂度为O(n)，如图4-12-2所示。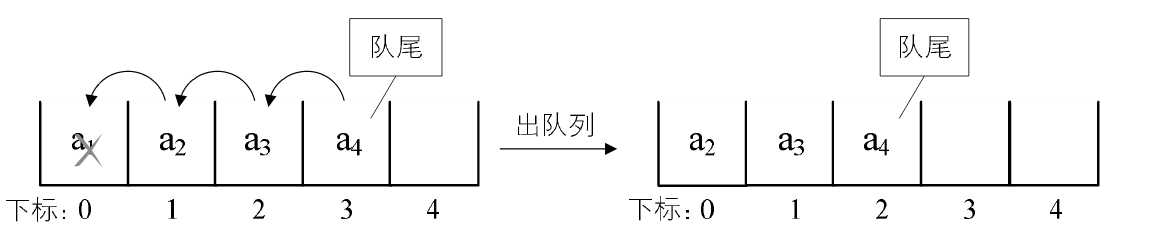
    image.png
    图4-12-2
    这里的实现和线性表的顺序存储结构(线性表挪动数组元素)完全相同，不再详述。

    在现实中也是如此，一群人在排队买票，前面的人买好了离开，后面的人就要全部向前一步，补上空位，似乎这也没什么不好。
    可有时想想，为什么出队列时一定要全部移动呢，如果不去限制队列的元素必须存储在数组的前n个单元这一条件，出队的性能就会大大增加。也就是说，队头不需要一定在下标为0的位置，如图4-12-3所示。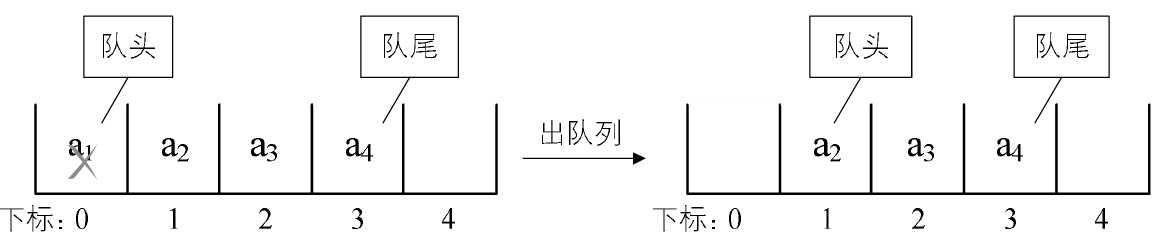
    image.png
    图4-12-3
    为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以引入两个指针，

    • front指针指向队头元素，
    • rear指针指向队尾元素的下一个位置，

    这样当front等于rear时，此队列不是还剩一个元素，而是空队列。

    假设是长度为5的数组，初始状态，空队列如图4-12-4的左图所示，front与rear指针均指向下标为0的位置。然后入队a 1 、a 2 、a 3 、a 4 ，front指针依然指向下标为0位置，而rear指针指向下标为4的位置，如图4-12-4的右图所示。
    image.png
    图4-12-4
    出队a 1 、a 2 ，则front指针指向下标为2的位置，rear不变，如图4-12-5的左图所示，再入队a5 ，此时front指针不变，rear指针移动到数组之外。嗯？数组之外，那将是哪里？如图4-12-5的右图所示。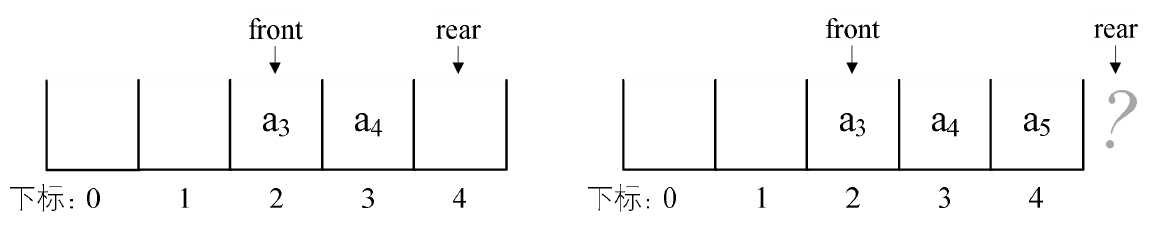
    image.png
    图4-12-5
    问题还不止于此。假设这个队列的总个数不超过5个，但目前如果接着入队的话，因数组末尾元素已经占用，再向后加，就会产生数组越界的错误，可实际上，我们的队列在下标为0和1的地方还是空闲的。我们把这种现象叫做“假溢出”。

    现实当中，你上了公交车，发现前排有两个空座位，而后排所有座位都已经坐满，你会怎么做？立马下车，并对自己说，后面没座了，我等下一辆？
    没有这么笨的人，前面有座位，当然也是可以坐的，除非坐满了，才会考虑下一辆。