深度优先遍历（Depth_First_Search），也有称为深度优先搜索，简称为DFS。

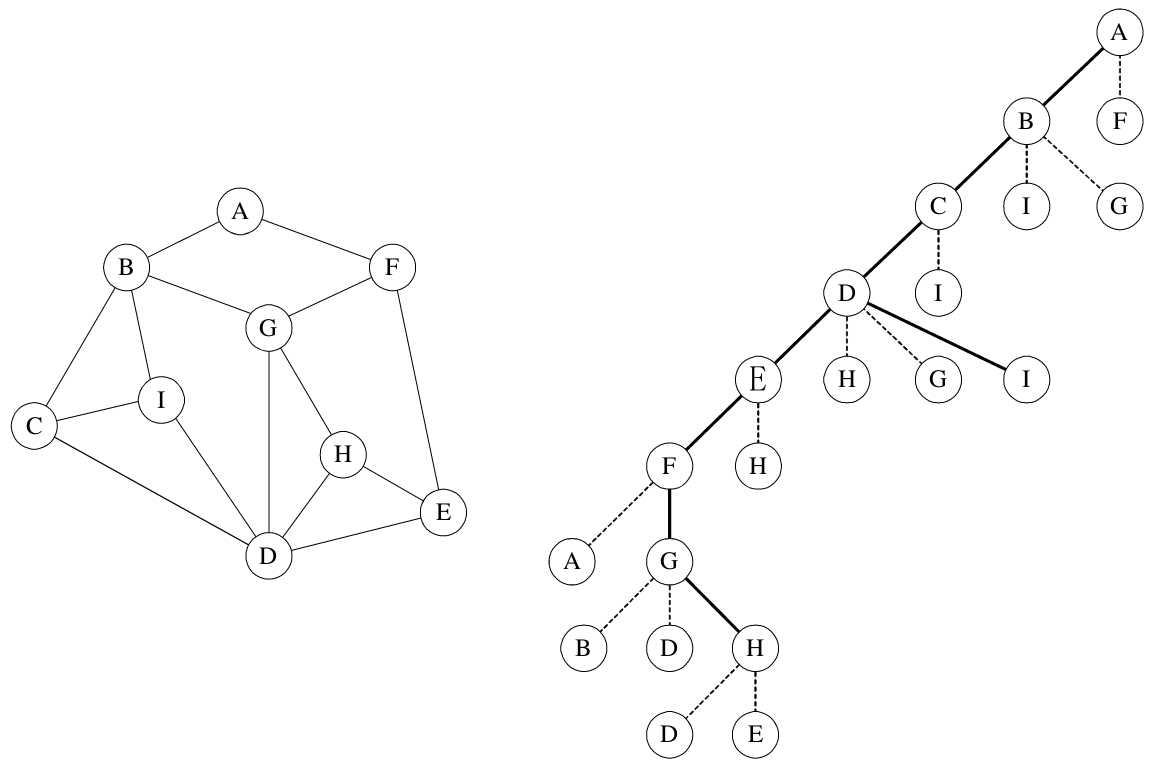
    image.png
    图7-5-2

    反应快的同学一定会感觉到，深度优先遍历其实就是一个递归的过程，
    如果再敏感一些，会发现其实转换成如图7-5-2的右图后，就像是一棵树的前序遍历，

    没错，它就是。它从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。
    事实上，我们这里讲到的是连通图，对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

    1. //如果我们用的是邻接矩阵的方式，则代码如下：
    3. /* Boolean是布尔类型，其值是TRUE或FALSE */
    4. typedef int Boolean;             
    6. /* 访问标志的数组 */
    7. Boolean visited[MAX];            
    9. /* 邻接矩阵的深度优先递归算法 */
    10. void DFS(MGraph G, int i)
    11. {
    12.     int j;
    14.     visited[i] = TRUE;
    16.     /* 打印顶点，也可以其他操作 */
    17.     printf("%c ", G.vexs[i]);    
    19.     for (j = 0; j < G.numVertexes; j++)
    20.         if (G.arc[i][j] == 1 && !visited[j])
    21.             /* 对为访问的邻接顶点递归调用 */
    22.             DFS(G, j);           
    23. }
    25. /* 邻接矩阵的深度遍历操作 */
    26. void DFSTraverse(MGraph G)
    27. {
    28.     int i;
    29.     for (i = 0; i < G.numVertexes; i++)
    30.         /* 初始所有顶点状态都是未访问过状态 */
    31.         visited[i] = FALSE;      
    33.     for (i = 0; i < G.numVertexes; i++)
    34.         /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */
    35.         if (!visited[i])         
    36.             DFS(G, i);
    37. }
    1. //如果图结构是邻接表结构，其DFSTraverse函数的代码是几乎相同的，只是在递归函数中因为将数组换成了链表而有不同，代码如下。
    3. /* 邻接表的深度优先递归算法 */
    4. void DFS(GraphAdjList GL, int i)
    5. {
    6.     EdgeNode *p;
    8.     visited[i] = TRUE;
    10.     /* 打印顶点，也可以其他操作 */
    11.     printf("%c ", GL->adjList[i].data);    
    13.     p = GL->adjList[i].firstedge;
    15.     while (p)
    16.     {
    17.         if (!visited[p->adjvex])
    18.             /* 对为访问的邻接顶点递归调用 */
    19.             DFS(GL, p->adjvex);            
    20.         p = p->next;
    21.     }
    22. }
    24. /* 邻接表的深度遍历操作 */
    25. void DFSTraverse(GraphAdjList GL)
    26. {
    27.     int i;
    29.     for (i = 0; i < GL->numVertexes; i++)
    30.         /* 初始所有顶点状态都是未访问过状态 */
    31.         visited[i] = FALSE;                
    33.     for (i = 0; i < GL->numVertexes; i++)
    34.         /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */
    35.         if (!visited[i])                   
    36.             DFS(GL, i);
    37. }

    对比两个不同存储结构的深度优先遍历算法，

    • 对于n个顶点e条边的图来说，邻接矩阵由于是二维数组，要查找每个顶点的邻接点需要访问矩阵中的所有元素，因此都需要O(n2)的时间。
    • 而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是O(n+e)。

    显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

    对于有向图而言，由于它只是对通道存在可行或不可行，算法上没有变化，是完全可以通用的。这里就不再详述了。