我们把这种指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树（Threaded Binary Tree）。

    image.png
    首先我们要来看看这空指针有多少个呢？

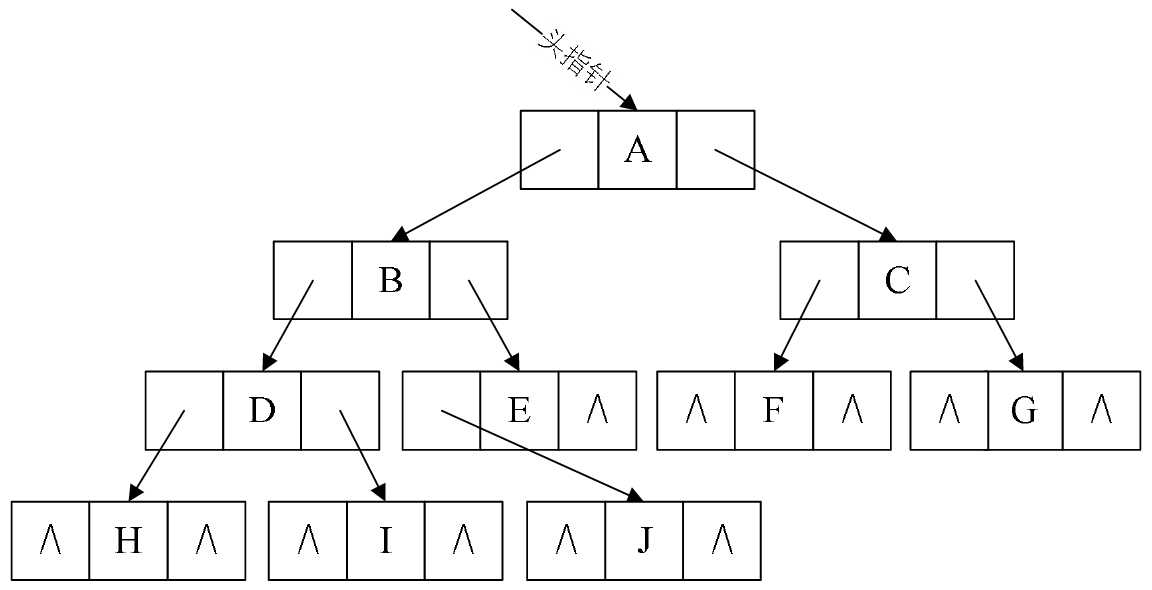
    image.png
    图6-10-1

    比如图6-10-1有10个结点，而带有“∧”空指针域为11。这些空间不存储任何事物，白白的浪费着内存的资源。
    另一方面，我们在做遍历时，比如对图6-10-1做中序遍历时，得到了HDIBJEAFCG这样的字符序列，遍历过后，我们可以知道，结点I的前驱是D，后继是B，结点F的前驱是A，后继是C。
    也就是说，我们可以很清楚的知道任意一个结点，它的前驱和后继是哪一个。

    请看图6-10-2，我们把这棵二叉树进行中序遍历后，将所有的空指针域中的rchild，改为指向它的后继结点。
    于是我们就可以通过指针知道H的后继是D（图中①），I的后继是B（图中②），J的后继是E（图中③），E的后继是A（图中④），F的后继是C（图中⑤），G的后继因为不存在而指向NULL（图中⑥）。
    此时共有6个空指针域被利用。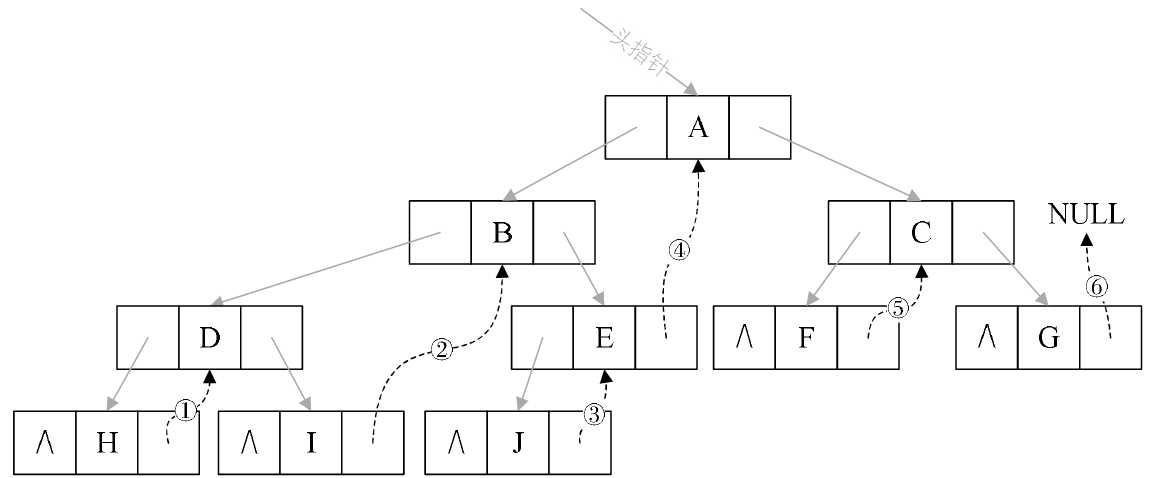
    image.png
    图6-10-2
    再看图6-10-3，我们将这棵二叉树的所有空指针域中的lchild，改为指向当前结点的前驱。
    因此H的前驱是NULL（图中①），I的前驱是D（图中②），J的前驱是B（图中③），F的前驱是A（图中④），G的前驱是C（图中⑤）。
    一共5个空指针域被利用，正好和上面的后继加起来是11个。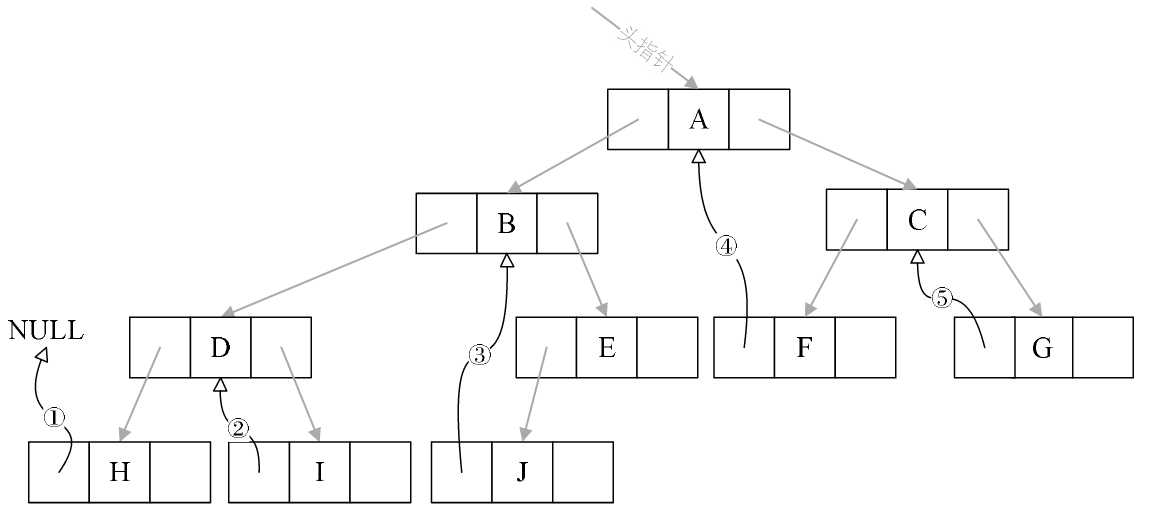
    image.png
    图6-10-3

    通过图6-10-4（空心箭头实线为前驱，虚线黑箭头为后继），就更容易看出，其实线索二叉树，等于是把一棵二叉树转变成了一个双向链表，这样对我们的插入删除结点、查找某个结点都带来了方便。

    所以我们对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化。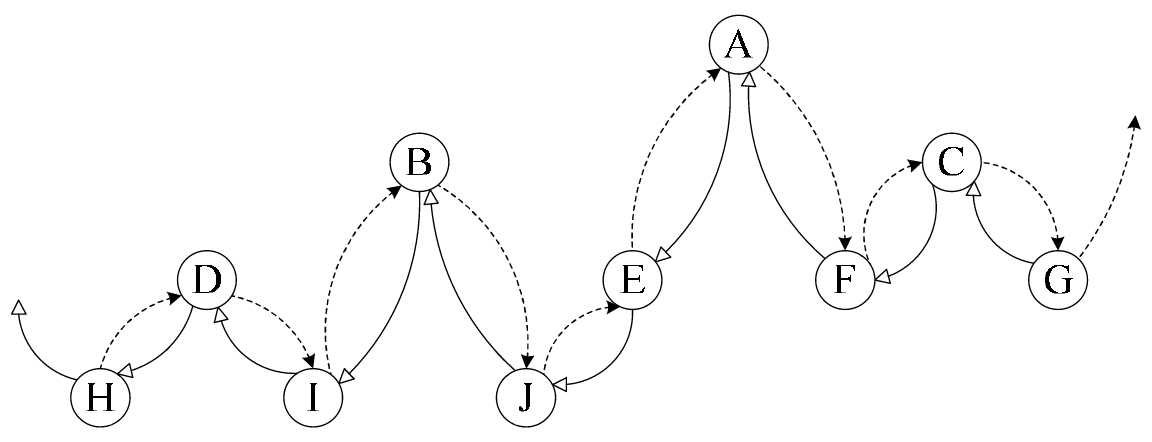
    image.png
    图6-10-4

    不过好事总是多磨的，问题并没有彻底解决。
    我们如何知道某一结点的
    lchild是指向它的左孩子还是指向前驱？
    rchild是指向右孩子还是指向后继？
    比如E结点的lchild是指向它的左孩子J，而rchild却是指向它的后继A。
    显然我们在决定lchild是指向左孩子还是前驱，rchild是指向右孩子还是后继上是需要一个区分标志的。
    因此，我们在每个结点再增设两个标志域ltag和rtag，注意ltag和rtag只是存放0或1数字的布尔型变量，其占用的内存空间要小于像lchild和rchild的指针变量。结点结构如表6-10-1所示。
    image.png
    表6-10-1
    其中：

    • ltag为0时指向该结点的左孩子，为1时指向该结点的前驱。
    • rtag为0时指向该结点的右孩子，为1时指向该结点的后继。
    • 因此对于图6-10-1的二叉链表图可以修改为图6-10-5的样子。

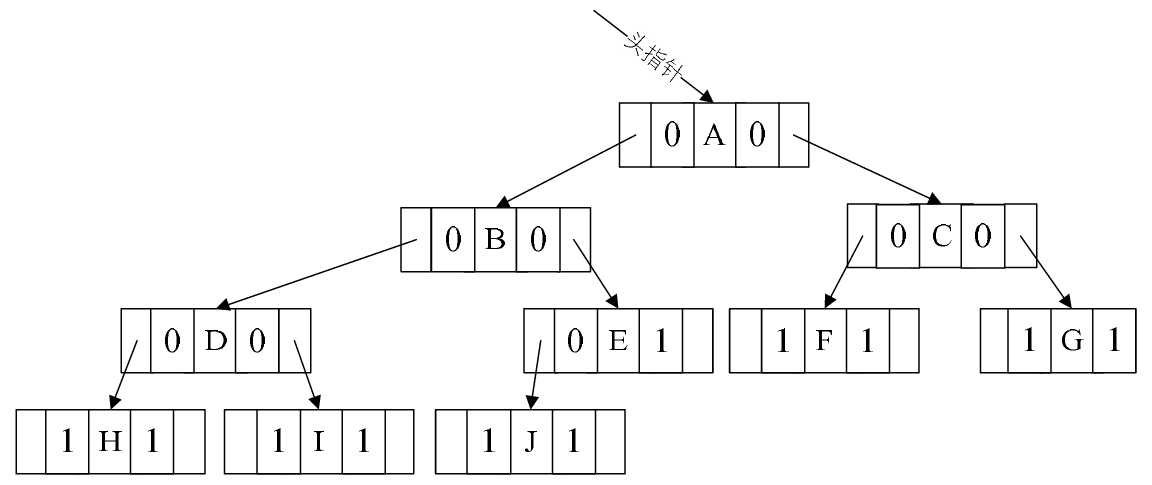
    image.png
    图6-10-5