由此二叉树的线索存储结构定义代码如下：

thread 线

英 [θred]

  1. /* 二叉树的二叉线索存储结构定义 */
  3. /* Link==0表示指向左右孩子指针 */
  4. /* Thread==1表示指向前驱或后继的线索 */
  5. typedef enum {Link, Thread} PointerTag;  
  7. /* 二叉线索存储结点结构 */
  8. typedef struct BiThrNode                   
  9. {
  10.     /* 结点数据 */
  11.     TElemType data;                        
  13.     /* 左右孩子指针 */
  14.     struct BiThrNode *lchild, *rchild;     
  16.     PointerTag LTag;
  17.     /* 左右标志 */
  18.     PointerTag RTag;                       
  20. } BiThrNode, *BiThrTree;

线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。
由于前驱和后继的信息只有在遍历该二叉树时才能得到，所以线索化的过程就是在遍历的过程中修改空指针的过程。

中序遍历线索化的递归函数代码如下：

  1. BiThrTree pre;                     /* 全局变量，始终指向刚刚访问过的结点 */
  2. /* 中序遍历进行中序线索化 */
  3. void InThreading(BiThrTree p)
  4. {
  5.     if (p)
  6.     {
  7.         /* 递归左子树线索化 */
  8.         InThreading(p->lchild);    
  10.         /* 没有左孩子 */
  11.         if (!p->lchild)            
  12.         {
  13.             /* 前驱线索 */
  14.             p->LTag = Thread;      
  15.             /* 左孩子指针指向前驱 */
  16.             p->lchild = pre;       
  17.         }
  19.         /* 前驱没有右孩子 */
  20.         if (!pre->rchild)          
  21.         {
  22.             /* 后继线索 */
  23.             pre->RTag = Thread;    
  24.             /* 前驱右孩子指针指向后继（当前结点p） */
  25.             pre->rchild = p;       
  27.         }
  29.         /* 保持pre指向p的前驱 */
  30.         pre = p;                   
  32.         /* 递归右子树线索化 */
  33.         InThreading(p->rchild);    
  34.     }
  35. }

中间加粗部分代码是做了这样的一些事。

  • if(!p->lchild)表示如果某结点的左指针域为空，因为其前驱结点刚刚访问过，赋值给了pre，所以可以将pre赋值给p->lchild，并修改p->LTag=Thread（也就是定义为1）以完成前驱结点的线索化。
  • 后继就要稍稍麻烦一些。因为此时p结点的后继还没有访问到，因此只能对它的前驱结点pre的右指针rchild做判断，if(!pre->rchild)表示如果为空，则p就是pre的后继，于是pre->rchild=p，并且设置pre->RTag=Thread，完成后继结点的线索化。

完成前驱和后继的判断后，别忘记将当前的结点p赋值给pre，以便于下一次使用。

有了线索二叉树后，我们对它进行遍历时发现，其实就等于是操作一个双向链表结构。
和双向链表结构一样，在二叉树线索链表上添加一个头结点，如图6-10-6所示， 并令

  • 其lchild域的指针指向二叉树的根结点（图中的①），
  • 其rchild域的指针指向中序遍历时访问的最后一个结点（图中的②）。

反之，令二叉树的中序序列中的
第一个结点中，lchild域指针
和最后一个结点的rchild域指针
均指向头结点（图中的③和④）。
这样定义的好处就是我们

  • 既可以从第一个结点起顺后继进行遍历，
  • 也可以从最后一个结点起顺前驱进行遍历。

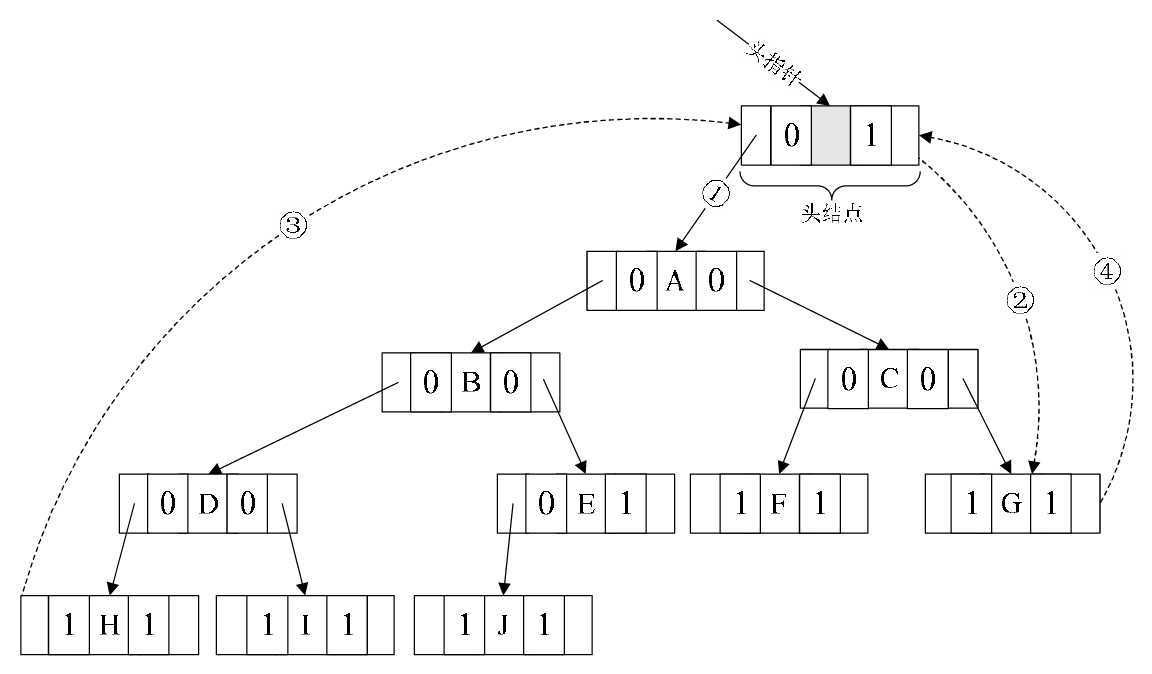
image.png
图6-10-6
遍历的代码如下：

  1. /* T指向头结点，头结点左链lchild指向根结点，
  2.                头结点右链rchild指向中序遍历的最后一个结点。
  3. /* 中序遍历二叉线索链表表示的二叉树T */
  5. Status InOrderTraverse_Thr(BiThrTree T)
  6. {
  7.     BiThrTree p;
  9.     /* p指向根结点 */
  10.     p = T->lchild;                 
  12.     /* 空树或遍历结束时，p==T */
  13.     while (p != T)                 
  14.     {
  15.         /* 当LTag==0时循环到中序序列第一个结点 */
  16.         while (p->LTag == Link)    
  17.             p = p->lchild;
  19.         /* 显示结点数据，可以更改为其他对结点操作 */
  20.         printf("%c", p->data);     
  22.         while (p->RTag == Thread && p->rchild != T)
  23.         {
  24.            p = p->rchild;
  25.            printf("%c", p->data);
  26.         }
  28.         /* p进至其右子树根 */
  29.         p = p->rchild;             
  30.    }
  31.    return OK;
  32. }
  1. 代码中，第10行，p=T->lchild;意思就是图6-10-6中的①，让p指向根结点开始遍历。
  2. 第13～30行，while(p!=T)其实意思就是循环直到图中的④的出现，此时意味着p指向了头结点，于是与T相等（T是指向头结点的指针），结束循环，否则一直循环下去进行遍历操作。
  3. 第16～17行，while(p->LTag==Link)这个循环，就是由A→B→D→H，此时H结点的LTag不是Link（就是不等于0），所以结束此循环。
  4. 第20行，打印H。

  5. 第22～26行，while(p->RTag==Thread&&p->rchild!=T)，由于结点H的RTag==Thread（就是等于1），且不是指向头结点。因此打印H的后继D，之后因为D的RTag是Link，因此退出循环。

  6. 第29行，p=p->rchild;意味着p指向了结点D的右孩子I。

  7. .……，就这样不断循环遍历，路径参照图6-10-4，直到打印出HDIBJEAFCG，结束遍历操作。

从这段代码也可以看出，它等于是一个链表的扫描，所以时间复杂度为O(n)。
由于它充分利用了空指针域的空间（这等于节省了空间），又保证了创建时的一次遍历就可以终生受用前驱后继的信息（这意味着节省了时间）。所以在实际问题中，如果所用的二叉树需经常遍历或查找结点时需要某种遍历序列中的前驱和后继，那么采用线索二叉链表的存储结构就是非常不错的选择。