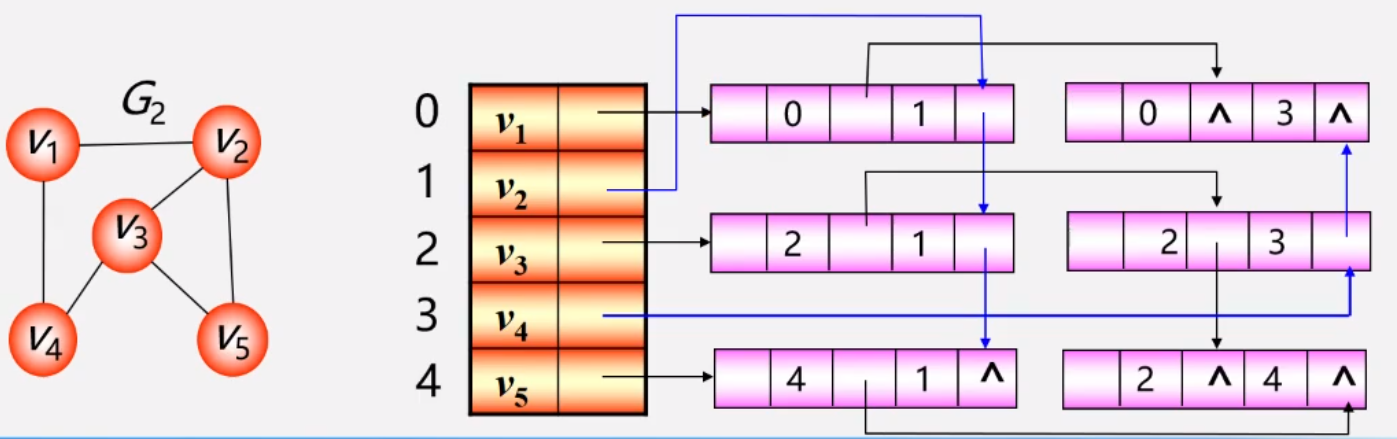
图的存储结构我们一共讲了五种,如图7-10-1所示,
其中比较重要的是邻接矩阵和邻接表,它们分别代表着边集是用数组还是链表的方式存储。
- 十字链表是针对有向图邻接表结构的优化,
- 邻接多重表是针对无向图邻接表结构的优化。
- 边集数组更多考虑的是对边的关注。
用什么存储结构需要具体问题具体分析,
通常稠密图,或读存数据较多,结构修改较少的图,用邻接矩阵要更合适,
反之则应该考虑邻接表。
十字链表(Orthogonal List)是有向图的另一种链式存储结构。
我们也可以把它看成是
- 将有向图的邻接表和逆邻接表结合起来形成的一种链表。
- 有向图中的每一条弧对应十字链表中的一个弧结点,同时有向图中的每个定点在十字链表中对应有一个结点,叫做定点结点。
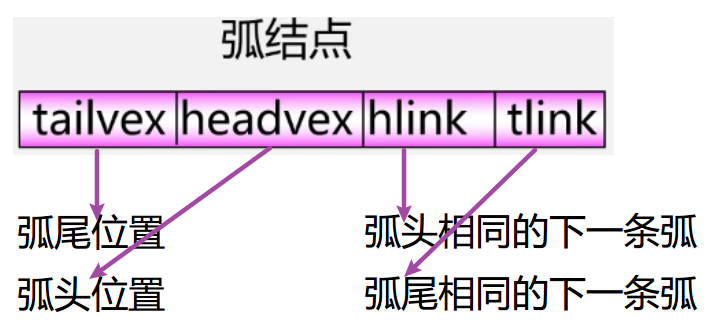
| data | firstin | firstout |
|---|---|---|
其中
- firstin表示入边表头指针,指向该顶点的入边表中第一个结点,
- firstout表示出边表头指针,指向该顶点的出边表中的第一个结点。
重新定义的边表结点结构如表所示。

其中
- tailvex是指弧起点在顶点表的下标,
- headvex是指弧终点在顶点表中的下标,
- headlink是指入边表指针域,指向终点相同的下一条边,
- taillink是指边表指针域,指向起点相同的下一条边。
如果是网,还可以再增加一个weight域来存储权值。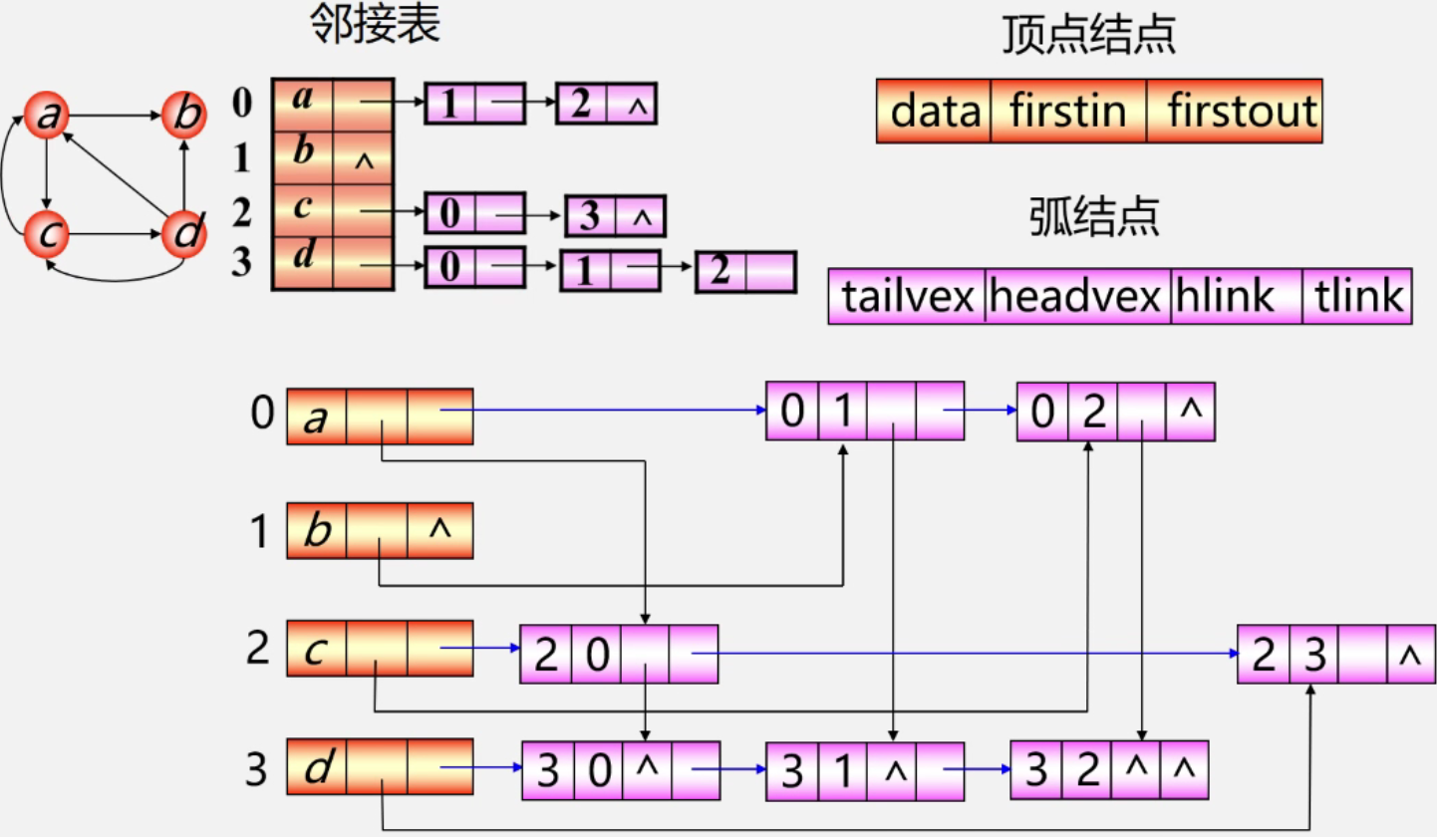
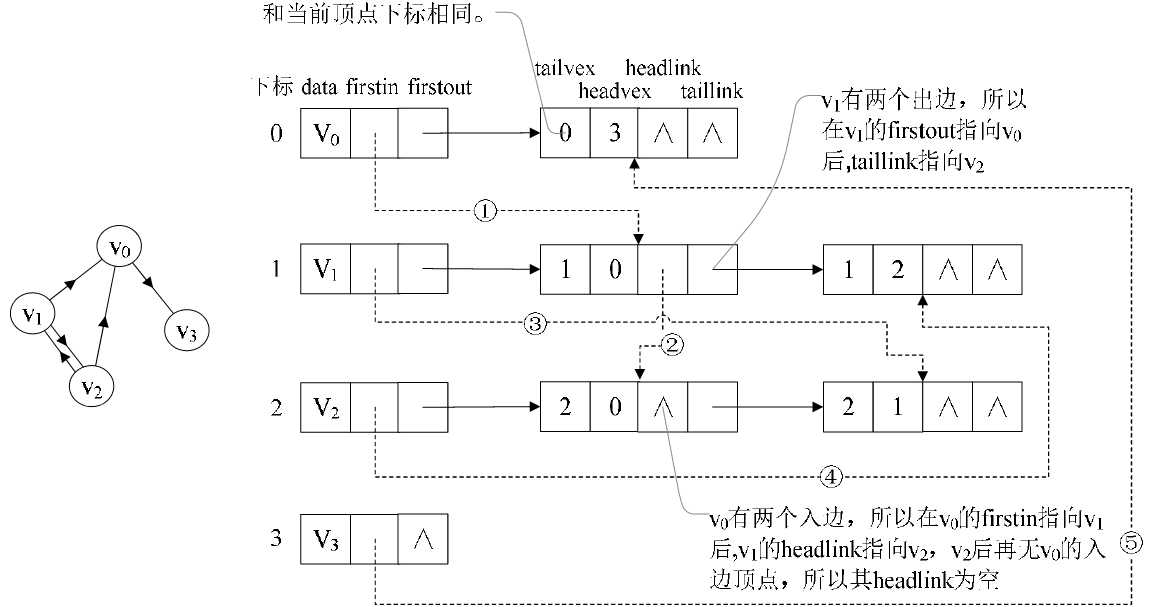
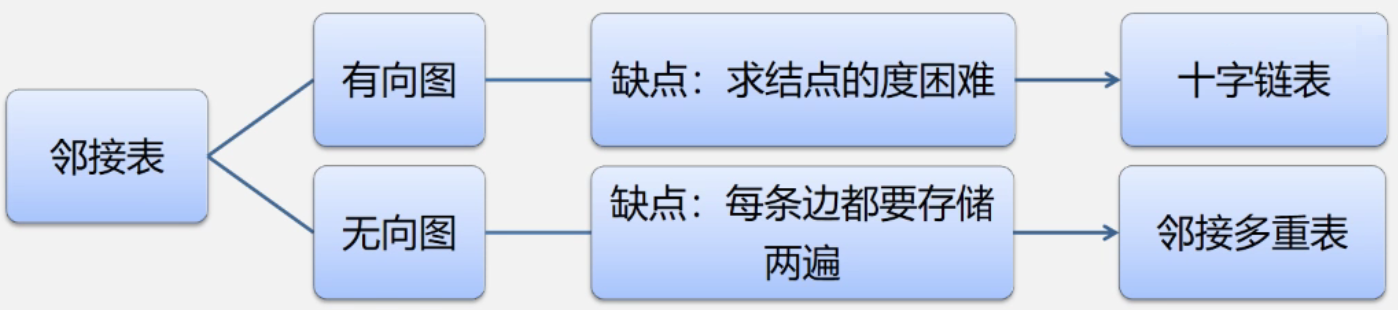
我们重点需要来解释虚线箭头的含义,它其实就是此图的逆邻接表的表示。
- 对于v 0 来说,它有两个顶点v 1 和v 2 的入边。
因此v 0 的firstin指向顶点v 1 的边表结点中headvex为0的结点,如图7-4-10右图中的①。
接着由入边结点的headlink指向下一个入边顶点v 2 ,如图中的②。
- 对于顶点v 1 ,它有一个入边顶点v 2 ,所以它的firstin指向顶点v 2 的边表结点中headvex为1的结点,如图中的③。
- 顶点v 2 和v 3 也是同样有一个入边顶点,如图中④和⑤。
十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以v i 为尾的弧,也容易找到以v i 为头的弧,因而容易求得顶点的出度和入度。
而且它除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的O(n+e),因此,在有向图的应用中,十字链表是非常好的数据结构模型。