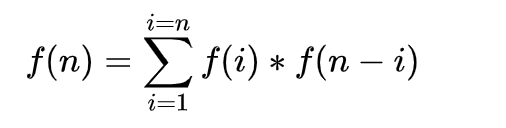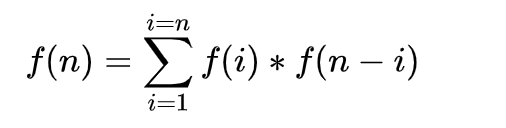0
f1=1
f2=2
f3=5
f4=14
f5 = f0f4 + f1f3 + f2f2 + f3f1 + f4*f0 = 14 + 5 + 4 + 5 + 14 = 42
卡特兰数
一、递推
我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出:
f(1) = 1 //即 1
f(2) = 2 //即 12、21
f(3) = 5 //即 123、132、213、321、231
然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d,
入栈顺序未知
出栈顺序未知,设置位置
那么考虑:元素a只可能出现在1号位置,2号位置,3号位置和4号位置(很容易理解,一共就4个位置,比如abcd,元素a就在1号位置)。
分析:i是i号位置,f(i-1)f(n-i)
1) 如果元素a在1号位置,那么只可能a进栈,马上出栈,此时还剩元素b、c、d等待操作,
就是子问题f(3);
如:0123、0132、0213、0321、0231
2) 如果元素a在2号位置,那么一定有一个元素比a先出栈,即有f(1)种可能顺序(只能是b),还剩c、d,即f(2),
根据乘法原理,一共的顺序个数为f(1) f(2);
3) 如果元素a在3号位置,那么一定有两个元素比1先出栈,即有f(2)种可能顺序(只能是b、c),还剩d,即f(1),
根据乘法原理,一共的顺序个数为f(2) f(1);
4) 如果元素a在4号位置,那么一定是a先进栈,最后出栈,那么元素b、c、d的出栈顺序即是此小问题的解,即
f(3);
结合所有情况,即f(4) = f(3) + f(2) f(1) + f(1) f(2) + f(3);
为了规整化,我们定义f(0) = 1;于是f(4)可以重新写为:
f(4) = f(0)f(3) + f(1)f(2) + f(2) f(1) + f(3)f(0) = 14
然后我们推广到n,推广思路和n=4时完全一样,于是我们可以得到:
f(n) = f(0)f(n-1) + f(1)f(n-2) + … + f(n-1)f(0)
即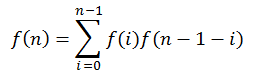
3.1 方法一:第一个入栈的元素是在什么时候出栈的?
3.2 方法二:最后一个出栈的元素是谁?最后一个出栈的元素是第几个进栈的元素
3.3 思路三

现在我要问问大家,这个最先进栈的元素,是不是就只能是最后出栈呢?
答案是不一定,要看什么情况。
栈对线性表的插入和删除的位置进行了限制,
并没有对元素进出的时间进行限制,
也就是说,在不是所有元素都进栈的情况下,事先进去的元素也可以出栈,只要保证是栈顶元素出栈就可以。
举例来说,如果我们现在是有3个整型数字元素1、2、3依次进栈,会有哪些出栈次序呢?
- 第一种:1、2、3进,再3、2、1出。这是最简单的最好理解的一种,出栈次序为321。
- 第二种:1进,1出,2进,2出,3进,3出。也就是进一个就出一个,出栈次序为123。
- 第三种:1进,2进,2出,1出,3进,3出。出栈次序为213。
- 第四种:1进,1出,2进,3进,3出,2出。出栈次序为132。
- 第五种:1进,2进,2出,3进,3出,1出。出栈次序为231。
有没有可能是312这样的次序出栈呢?答案是肯定不会。
因为3先出栈,就意味着,3曾经进栈,既然3都进栈了,那也就意味着,1和2已经进栈了,此时,2一定是在1的上面,就是更接近栈顶,那么出栈只可能是321,不然不满足123依次进栈的要求,所以此时不会发生1比2先出栈的情况。