Improved Adversarial Defense through Robust Bayesian Neural Network
本文是UCLA和UC Davis发表于ICLR 2019的工作,论文提出了一种新的对抗防御方法,结合了贝叶斯神经网络(BNN)和对抗训练的优势,获得了不错的效果。其中,BNN将每个权重参数视作一个随机变量,在预测时相当于一个无限个数的集成模型,实验证明只依靠BNN并不能做好防御,结合对抗训练才会提升模型的防御能力。
评:本文没有提出原创的方法,而是结合两种现有的方法进行了组合测试,取得了不错的效果。
1.前言
首先,尽管最近的研究表明引入随机性可以提高神经网络的稳定性,但是我们发现盲目地给各个层添加噪声不是引入随机性的最优方法。我们可通过贝叶斯神经网络来学习模型的后验分布。第二,我们建立的BNN中的最小最大问题来学习对抗攻击下的最优的模型分布,称为“对抗训练贝叶斯神经网络”。
2.PGD攻击
CW和PGD是公认的两种表现不俗的攻击方法。PGD攻击比CW攻击好的一点在于:PGD攻击可以通过改变γ 来直接控制干扰量,而CW攻击需要调整损失函数中的超参数c,这显然没有PGD更为直接。
PGD攻击的目标函数为: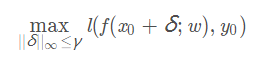
PGD攻击可以利用投影梯度下降来迭代更新对抗样本: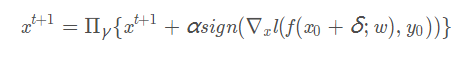
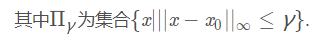
对于随机神经网络,攻击者试图寻找寻找一个通用的干扰来欺骗大多数随机权重。该通用干扰可最大化损失函数的期望来获得: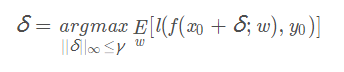
该优化问题与PGD和CW的求解方法类似,唯一的区别是我们需要在每次迭代时对w ww进行采样。
3.BNN
对于观测随机变量( x , y ) (x,y)(x,y),我们的目标是估计隐变量w ww的分布。给定先验分布p ( w ) p(w)p(w),后验分布为: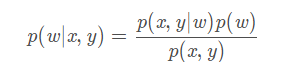
后验分布的分母是一个无穷积分,因此该后验分布很难计算。通常有两种处理方式:
(1)SGLD:在不知道闭式解的情况下采样w ∼ p ( w ∣ x , y ) w\sim p(w|x,y)w∼p(w∣x,y)
该方法的本质是带高斯噪声的随机梯度下降,很容易实现。但是每次minbatch迭代只能得到一个样本,对快速推断不是很有效。并且随着SGLD中步长ϵ t \epsilon{t}ϵt减小,样本之间的相关性增大,因此需要生成更多的样本来保证具有一定的方差。
(2)利用某一参数分布q θ ( w ) q{\theta}(w)_qθ(_w)来近似 p ( w ∣ x , y ) p(w|x,y)p(w∣x,y),其中θ \thetaθ的确定可通过最小化 K L ( q θ ( w ) ∣ ∣ p ( w ∣ x , y ) ) KL(q{\theta}(w)||p(w|x,y))_KL(q__θ(w)∣∣p(w∣x,y))
该变分推断是生成样本的有效方法,因为我们通过最小化KL散度后知道近似后验分布q θ ( w ) q{\theta}(w)q_θ(w)。为了简单起见,我们可以假设近似后验分布是全分解高斯分布: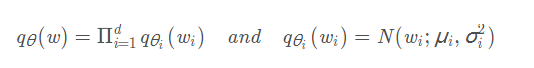
当变量之间相关性比较大时,该简单形式会导致q θ ( w ) q{\theta}(w)q_θ(w)与p ( w ∣ x , y ) p(w|x,y)p(w∣x,y)存在很大偏差。
4.adv-BNN
我们将对抗训练(Mardry 2017)与BNN结合起来。
对于任意两个高斯分布s ss和t tt,其KL-divergence为: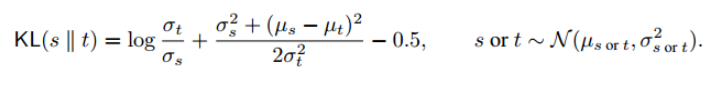
变分推断:
方法一:

摘要
提出了一种新的算法来训练抗对抗性攻击的鲁棒神经网络。我们的算法是由以下两个想法驱动的。首先,尽管最近的工作表明融合随机性可以提高神经网络的鲁棒性(Liu et al., 2017),但我们注意到,盲目地向所有层添加噪声并不是融合随机性的最佳方式。相反,我们在贝叶斯神经网络(BNN)框架下建模随机性,以一种可扩展的方式正式学习模型的后验分布。其次,我们在BNN中建立最小最大问题来学习在对抗攻击下的最佳模型分布,从而形成一个对抗训练的贝叶斯神经网络。实验结果表明,在较强的攻击下,该算法达到了最先进的性能。在使用VGG网络的CIFAR-10上,我们的模型在0:035失真的PGD攻击下,与对抗训练(Madry et al., 2017)和随机自集成(Liu et al., 2017)相比,准确率提高了14%,而在ImageNet1子集上,差距甚至更大。
深度神经网络已经在许多困难的机器学习任务中展示了最先进的性能。尽管深度神经网络在各种任务上取得了根本性的突破,但已经被证明在对抗攻击中完全是脆弱的(Szegedy等人,2013;Goodfellow等,2015)。精心设计的扰动可以添加到目标模型的输入中,以推动深层神经网络的性能达到随机水平。在图像分类的背景下,这些扰动是人眼无法察觉的,但会使分类模型预测到错误的类别。寻找这种扰动的算法被表示为对抗性攻击(Chen等人,2018;Carlini & Wagner, 2017b;Papernot等人,2017),一些攻击在物理世界中仍然有效(Kurakin等人,2017;Evtimov等,2017)。深度神经网络对对抗实例缺乏鲁棒性这一固有弱点引起了安全问题,特别是在要求高可靠性的安全敏感应用中。为了防止对抗例子和提高神经网络的鲁棒性,最近提出了许多算法(Papernot et al., 2016;Zantedeschi等人,2017;Kurakin等人,2017;黄等,2015;Xu等,2015)。其中,有两项工作显示了中型数据的有效结果(如CIFAR-10)。
第一行工作使用对抗训练来提高鲁棒性,最近在Madry等人(2017)中提出的算法被认为是最成功的防御之一,如Athalye等人(2018)所示。
第二种方法是在神经网络中加入随机成分,以隐藏梯度信息。在黑盒设置下,随机输出可以显著增加使用有限差分技术进行攻击的查询计数(Chen et al., 2018;Ilyas等人,2018年),甚至在白盒设置下,Liu等人(2017)最近提出的随机自集成(RSE)方法也达到了与Madry的对抗训练算法类似的性能。
本文提出了一种新的防御算法ad - bnn。这个想法是将对抗性训练和贝叶斯网络结合起来,尽管在对抗性攻击中尝试BNNs并不新鲜(例如:
(Li & Gal, 2017;Feinman等人,2017;Smith & Gal, 2018)),最近Ye & Zhu(2018)也尝试将贝叶斯学习与对抗性训练结合起来,这是我们第一次将问题扩展到复杂数据,我们的方法比以前的防御方法获得了更好的鲁棒性。
本文的贡献可以总结如下:
•我们不像在RSE中那样给每一层的输入添加随机性,而是直接假设网络中的所有权值都是随机的,并使用贝叶斯神经网络(BNN)中常用的技术进行训练。
•我们提出了一个新的最小最大公式,将对抗训练与BNN相结合,显示问题可以通过投影梯度下降和SGD之间的交替来解决。
•我们在CIFAR10、STL10和ImageNet143数据集上测试了提出的advn - bnn方法,并显示了与之前的方法(包括RSE和对抗训练)相比的显著改进
2背景
2.1对抗性的攻防在本节中,我们总结了对抗性攻防的相关工作。
攻击:大多数算法基于相对于输入的损失函数梯度生成对抗性的例子。例如,FGSM (Goodfellow等人,2015)通过梯度的符号对一个例子进行扰动,并使用步长来控制扰动的‘1范数。Kurakin等人(2017)提出运行FGSM的多次迭代。最近,C&W攻击Carlini & Wagner (2017a)正式将攻击作为一个优化问题提出,并应用基于梯度的迭代求解器来获得一个对抗的例子。C&W攻击和PGD攻击(Madry et al., 2017)由于其有效性,经常被用于基准防御算法(Athalye et al., 2018)。
在整个过程中,我们以PGD攻击为例,主要遵循Madry et al.(2017)。
PGD攻击的目标是在γ-球中寻找对抗的例子,可以自然地表述为以下目标函数:
防御:近年来提出了多种多样的防御方法,如基于去噪器的高分辨率图像处理(Liao et al., 2017)和随机图像预处理(Xie et al., 2017)。读者可以从库拉金等人(2018)那里找到更多信息。下面我们选择了两个对白盒攻击有效的具有代表性的方法。它们是我们实验的主要基线。
第一个例子是对抗性训练(Szegedy et al., 2013;Goodfellow等,2015)。它本质上是一种数据增强方法,通过对抗性的例子训练深度神经网络,直到损失收敛。Madry等人(2017)提出将对抗性搜索纳入训练过程,解决了以下鲁棒优化问题,而不是搜索对抗性实例并将其添加到训练数据中:
其中Dtr为训练数据分布。通过使用PGD攻击生成对抗例,然后最小化对抗例的分类损失,近似解决了上述问题。在本文中,我们建议在贝叶斯神经网络中加入对抗训练以获得更好的鲁棒性。
另一个例子是RSE (Liu et al., 2017),在该算法中,作者提出了一个“噪声层”,将输入特征与高斯噪声融合。他们根据经验表明,模型的集合可以增加深度神经网络的鲁棒性。此外,他们的方法可以在不增加任何内存成本的情况下实时生成无限个模型。由于在训练和测试阶段都使用了噪声层,所以对预测精度的影响不大。我们的算法与RSE有两个不同之处:1)我们在每个权值上加入噪声而不是输入或隐藏特征,并将其正式建模为BNN。2)我们采用对抗性训练来进一步提高成绩。
2.2贝叶斯神经网络(BNN)-0.8
0.4
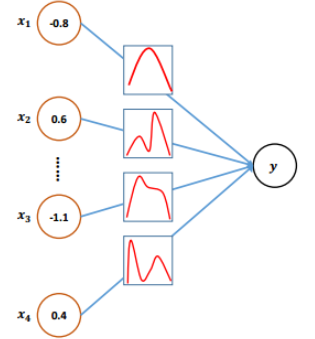
0.6 - -1.1𝒚……𝒙𝟏𝒙𝟐𝒙𝟑𝒙𝟒图1:贝叶斯神经网络的说明。
图1说明了BNN的思想。给定可观察随机变量(x;y),我们的目标是估计隐藏变量w的分布。在我们的情况下,可观察随机变量对应于特征x和标签y,我们感兴趣的是权重p(wjx;y)已知先验p(w)然而,后验的精确解往往是难以解决的:注意p(wjx;y) = p(x;yjw)p(w)p(x;y)但分母涉及高维积分(Blei et al., 2017),因此条件概率很难计算。
为了加速推理,我们通常有两种方法——我们可以对w和p(wjx;y)有效地不需要知道封闭形式的公式,例如随机梯度朗之万动力学(SGLD) (Welling & Teh, 2011),或者我们可以近似真实的后置p(wjx;其中未知参数θ通过最小化KLqθ(w) k p(wjx)估计;y) θ。
神经网络中,kl散度的精确形式是无法获得的,但我们可以很容易地通过反向传播找到它的无偏梯度估计,即通过Backprop的贝叶斯(Blundell et al., 2015)。
尽管这两种方法都得到了广泛的应用和深入的分析,但都存在一些明显的缺陷,使得高维贝叶斯推理仍然是一个有待解决的问题。对于SGLD及其扩展(例如(Li et al., 2016)),由于算法本质上是带有额外高斯噪声的SGD更新,所以它们非常容易实现。然而,他们只能得到一个样本w∼p(wjx;y)在每个小批迭代中以一个前向向后传播为代价,因此对于快速推理来说效率不够。此外,随着SGLD中的步长ηt的减小,样品之间的相关性越来越强,需要生成很多样品来控制方差。相反,变分推理方法是有效的生成样本,因为我们知道,一旦我们最小化kl散度后验qθ(w)。问题是,为了简单起见,我们通常假设近似qθ是一个完全分解的高斯分布:

