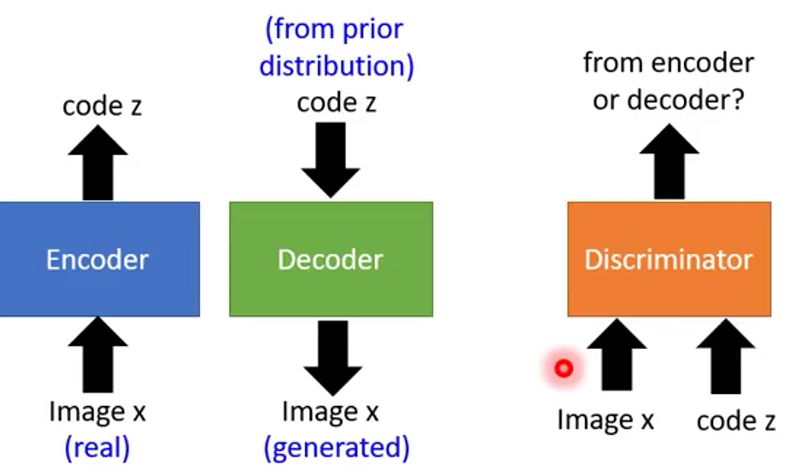
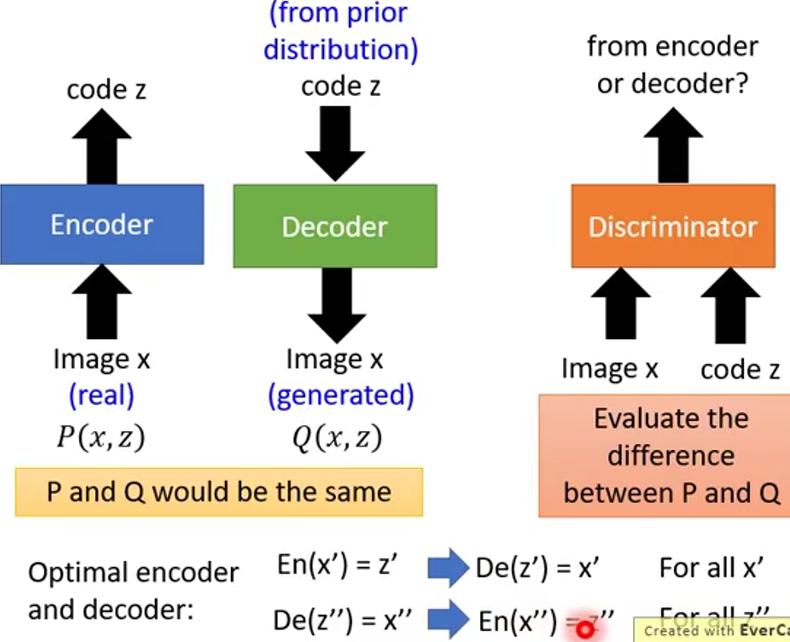
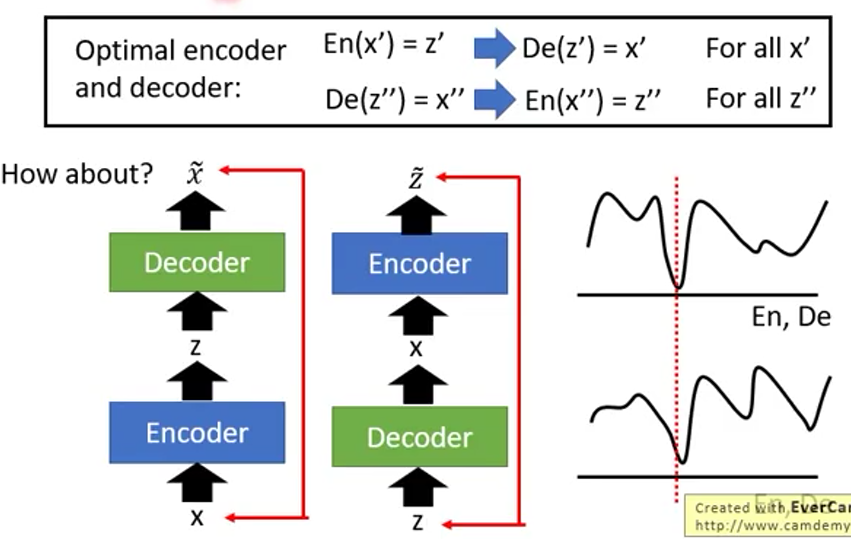
生成对抗网络（GAN，Generative Adversarial Networks）：生成式模型

• 不依赖任何先验假设。传统的许多方法会假设数据服从某一分布，然后使用极大似然去估计数据分布。
• 生成real-like样本的方式非常简单。GAN生成real-like样本的方式通过生成器(Generator)的前向传播，而传统方法的采样方式非常复杂，有

  1.1原理

  已知真实图片集的分布，生成也在这个分布内的图片
  （真实分布中取出一些数据，）
  
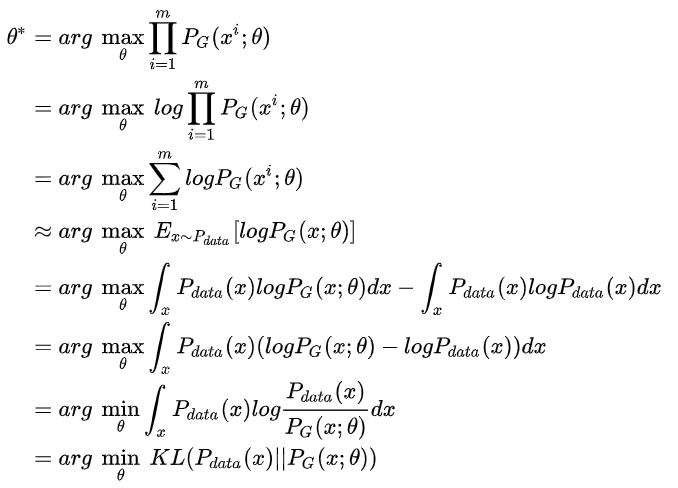
  所以最大化似然，让generator最大概率的生成真实图片，也就是要找一个让更接近于
  那如何来找这个最合理的呢？我们可以假设是一个神经网络。
  

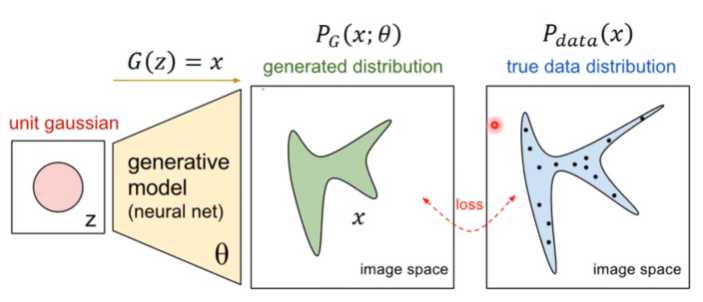
现在我们先固定G，来求解最优的D


把最优的D带入


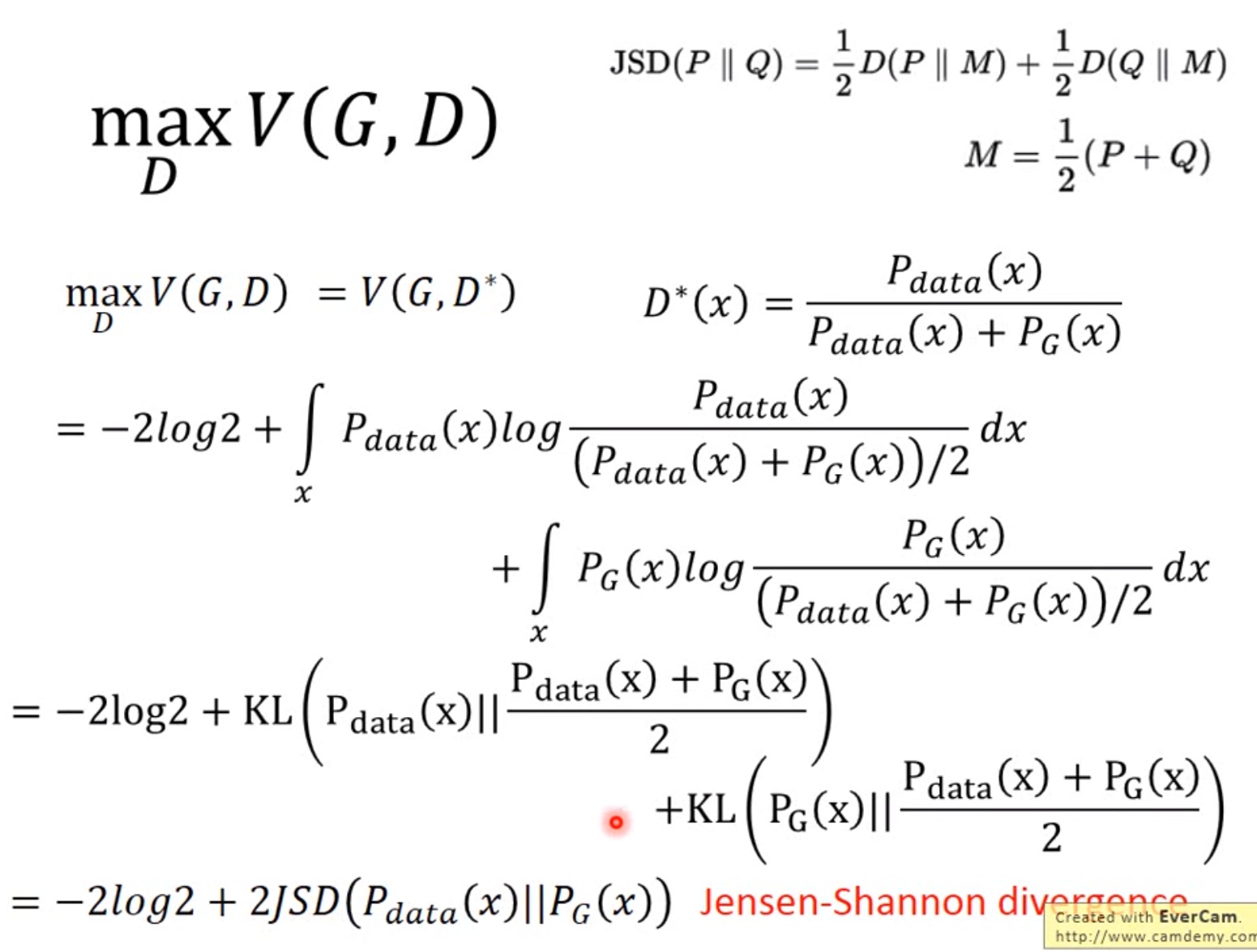
公式推导说明：固定G，表示两个分布之间的差异，最小值是-2log2，最大值为0。
现在找G，来最小化，观察上式，当时，G是最优的。

有了上面推导的基础之后，我们就可以开始训练GAN了。
1.训练，存在问题

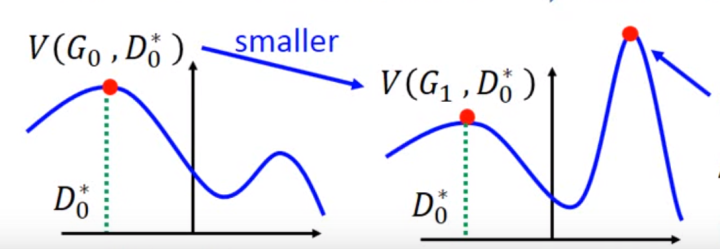
避免上述情况的方法就是更新G的时候，不要更新G太多。

1.2.为什么是高斯函数

最大熵原理

熵

• 熵(entropy)是热力学中的概念,由香浓引入到信息论中。在信息论和概率统计中,熵用来表示随机变量不确定性的度量。

• H(x)依赖于X的分布,而与X的具体值无关。H(X)越大,表示X的
  不确定性越大。

最大熵模型（The Maximum Entropy）
从信息论的角度讲，就是保留了最大的不确定性，也就是让熵达到最大。
当我们需要对一个事件的概率分布进行预测时，最大熵原理告诉我们所有的预测应当满足全部已知的条件，而对未知的情况不要做任何主观假设（不做主观假设这点很重要）。也就是让概率分布最均匀，预测的风险最小。

高斯分布代表一种无知的状态。
当我们所知道有关变量的信息仅仅是它们的均值和方差时，那么高斯分布便是我们唯一的选择。也就是说高斯分布是我们无知状态的最自然的表达，因为如果我们所愿意假设的仅是分布的均值和方差，那么高斯分布是可以以最多种方式实现这一目标的形状，同时不引入任何新的假设。通过这种方式，高斯分布是与我们的假设最一致的分布。

1.3.目标函数（不同的距离量度）

f-divergence

LSGAN

IPM

WGAN

the problem of JS divergence

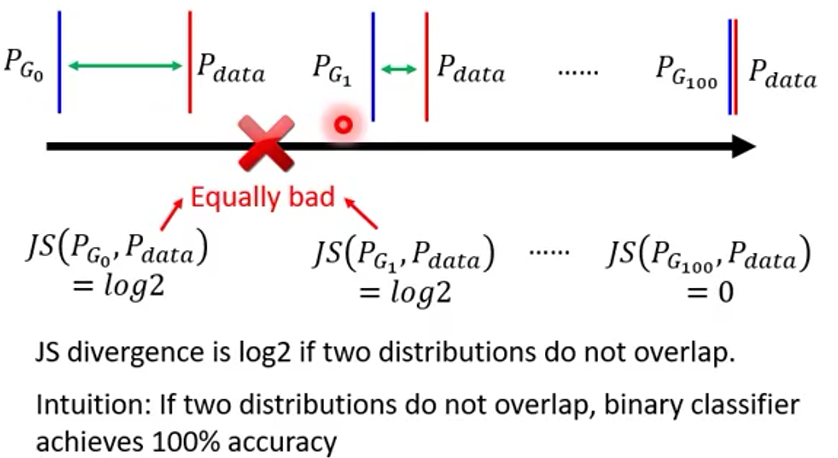
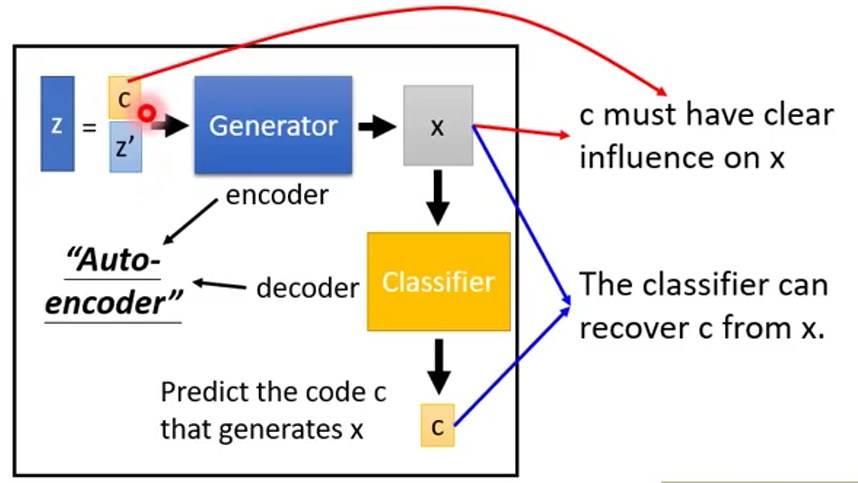
InfoGAN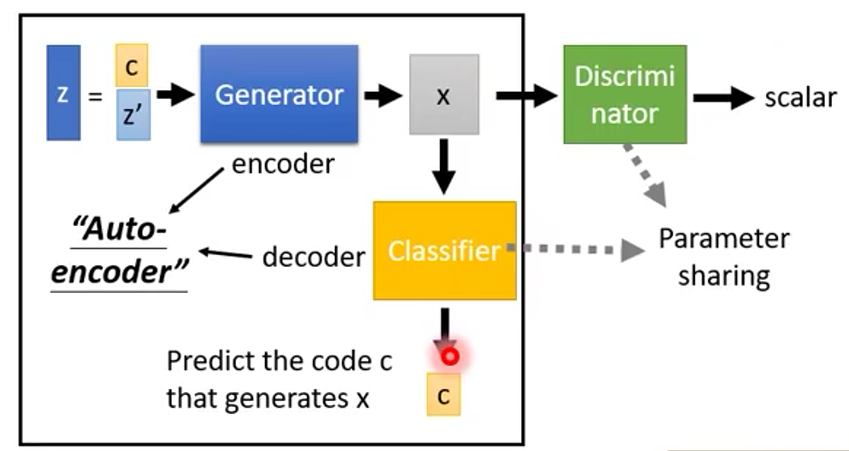


VAE-GAN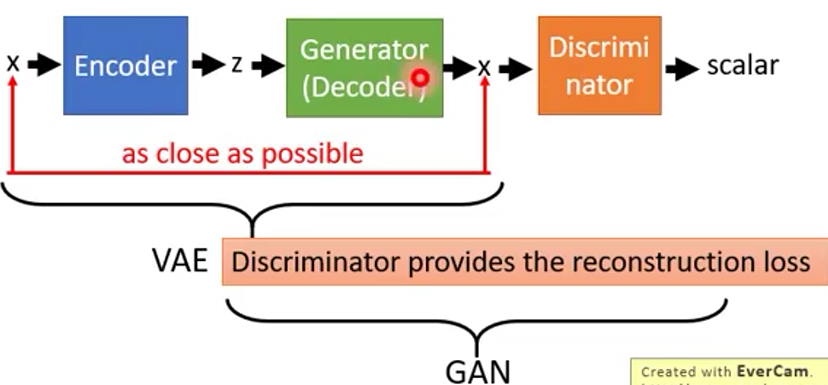

BIGAN(2)

2. 其他常见生成式模型