一、概述

假设有如下数据：

:observed data :unobserved data(latent variable) :complete data :parameter

EM算法的目的是解决具有隐变量的参数估计（MLE、MAP）问题。EM算法是一种迭代更新的算法，其计算公式为：

这个公式包含了迭代的两步：
①E step：计算在概率分布下的期望
②S step：计算使这个期望最大化的参数得到下一个EM步骤的输入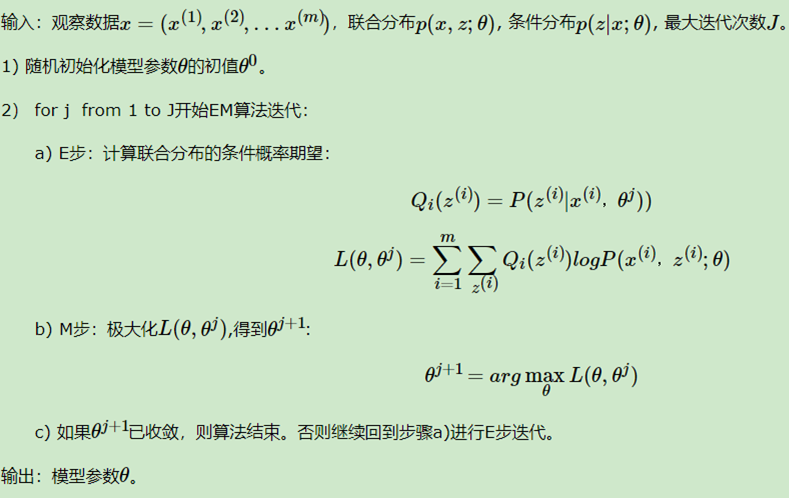

二、EM的算法收敛性

现在要证明迭代求得的序列会使得对应的是单调递增的，也就是说要证明。首先我们有：

接下来等式两边同时求关于的期望：

这里我们定义了，称为Q函数（Q function），这个函数也就是上面的概述中迭代公式里用到的函数，因此满足。
接下来将上面的等式两边分别取和并相减：

我们需要证明，同时已知，现在来观察：

因此得证。这说明使用EM算法迭代更新参数可以使得逐步增大。
另外还有其他定理保证了EM的算法收敛性。首先对于序列和其对应的对数似然序列有如下定理：
①如果有上界，则收敛到某一值；
②在函数与满足一定条件下，由EM算法得到的参数估计序列的收敛值是的稳定点。

三、EM的算法的导出

1. ELBO+KL散度的方法

   

因此我们得出，由于KL散度恒，因此，则就是似然函数的下界。
使得时，就必须有，也就是时。
在每次迭代中我们取，就可以保证与相等，也就是：

也就是说与都是关于的函数，且满足，也就是说的图像总是在的图像的上面。对于，我们取，这也就保证了只有在时与才会相等，因此使取极大值的一定能使得。该过程如下图所示：

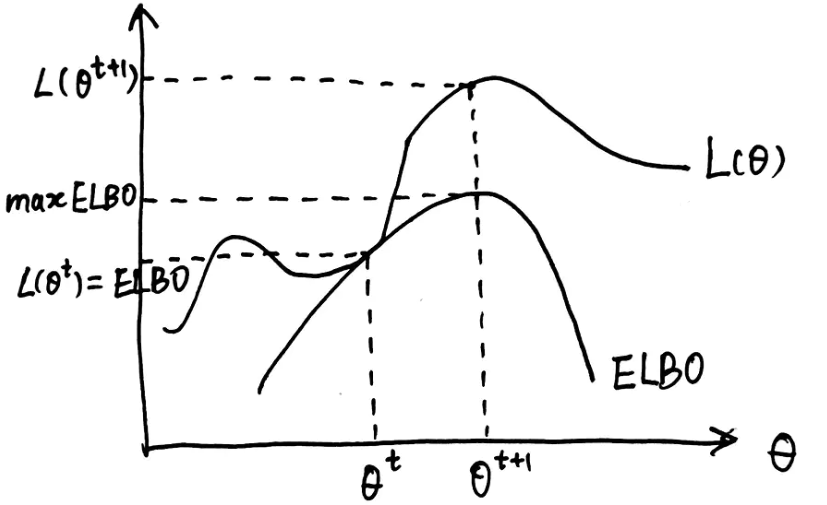
ELBO
然后我们观察一下取极大值的过程：

由此我们就导出了EM算法的迭代公式。

1. ELBO+Jensen不等式的方法

首先要具体介绍一下Jensen不等式：对于一个凹函数 （国内外对凹凸函数的定义恰好相反，这里的凹函数指的是国外定义的凹函数），我们查看其图像如下：

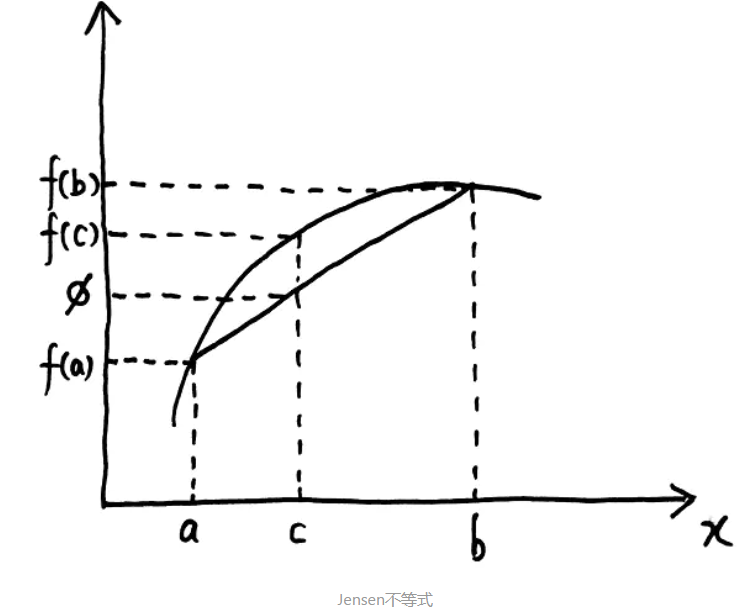
Jensen不等式

接下来应用Jensen不等式来导出EM算法：

这里应用了Jensen不等式得到了上面出现过的，这里的函数也就是函数，显然这是一个凹函数。当这个函数是一个常数时会取得等号：

这种方法到这里就和上面的方法一样了，总结来说就是：

参考：
博客1
博客2
机器学习——聚类