隐马尔可夫模型的概率图模型如下：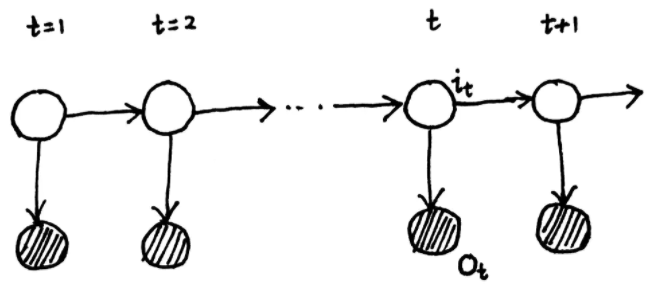

概率图模型
上图中代表时刻，阴影部分为观测变量序列，非阴影部分为状态变量序列，另外我们定义观测变量取值的集合为，状态变量取值的集合为：

隐马尔可夫模型的参数用表达：

其中为初始概率分布，是一个多维向量；为状态转移矩阵；为发射矩阵：

3. 两个假设

• 齐次马尔可夫假设

任意时刻的状态只依赖于前一时刻的状态，即：

• 观测独立假设

任意时刻的观测只依赖于当前时刻的状态，即：

4. 三个问题

• Evaluation

已知模型的参数，计算某个观测序列发生的概率，即求：

• Learning

已知观测序列，使用EM算法求参数：

• Decoding

已知观测序列和参数，求使概率最大的状态序列，即：

具体实例：命名实体识别

HMM模型
learning：

参数

其中为初始概率分布，是一个多维向量；
为状态转移矩阵；
为发射矩阵：
HMM参数学习(监督学习): 用现在有一些文本和与之对应的标注数据, 来训练一个HMM来拟合这些数据
Inference的Decoding：