研究相关 - 用于评估神经图像分割算法的性能指标表征 - 《ML学习笔记》

简介

Performance measure characterization for evaluating neuroimage segmentation algorithms

摘要
由于神经解剖结构的复杂性，图像的质量以及对精确分割的要求，表征脑图像中分割算法的性能一直是一个持续的挑战。使用与敏感性和特异性相关的Jaccard和Dice相似系数来评估分割算法的性能引起了很多兴趣。本文讨论了评估框架中采用的基本绩效指标的基本特征。在探索“ Jaccard”，“ Dice”和“ Specificity”系数的属性的同时，我们提出了新的度量系数“一致性Conformity和敏感性”，用于评估图像分割技术。结果表明，Conformity比Jaccard和Dice更为敏感和严格，因为它在检测分割图像中的细微变化方面具有更好的判别能力。与特异性相比，灵敏度可提供一致且可靠的评估分数，而无需结合图像背景属性。通过使用各种分割技术提取各种各样的大脑图像中的神经解剖结构，可以说明所提出系数的优点。

简介

图像分割是将图像划分为有意义的对象的过程，以便每个区域都具有由其灰度和纹理反映的相似特征。这是神经图像分析（例如特征提取，形状表示和测量以及图像理解）中的关键预处理步骤。随着医学成像模式的速度和分辨率的最新进步以及对脑成像程序的需求的不断增长，促进图像数据处理和分析的计算机辅助已变得重要和必要。在许多临床和研究应用中，对脑图像中的解剖和病理结构进行分割的需求已大大增加，例如病理学的定位，定量的体积评估，外科治疗计划，计算机辅助的诊断和外科手术，脑图，血管图和 3-D可视化（Heinonen等，1999; Pham等，2000; Suri等，2002; Toga和Mazziotta，2002; Ashburner和Friston，2005; Joshi等，2007）。
几十年来，已经提出了各种各样的人和动物脑图像分割技术，包括基于阈值，基于区域，基于统计信息，分类，可变形模型，图集指导的技术和基于知识的方法（Frangi等人等人，1999； Pham等人，2000； Kaus等人，2001； Dogdas等人，2005； Sharief等人，2008）。迄今为止，还没有普遍接受的分割技术可以在广泛的神经图像处理应用中产生令人满意的结果。大多数算法做出的基本假设限制了它们在特定问题和应用中的使用（Dawant等人，1999； MacDonald等人，2000； Ali等人，2005； Wu等人，2006； Kloppel等人，2008）。尽管分割仍然是脑图像分析中一个具有挑战性的问题，但分割算法评估的发展一直滞后（Udupa等，2006）。
可以想象，这种滞后是由于难以定义性能系数和统计数据，难以建立金标准以及难以收集冗长而费时的数据（Haralick，1994年； Chalana和Kim，1997年； Udupa等人，2006年）导致的）。
然而，已经提出了许多评估方法。
Zhang（1996）提出了一种评估方法的理想特性，包括研究不同分割算法的通用性，定量测量的能力和客观评估能力。客观研究应排除人为因素的影响，并提供一致和公正的结果。此外，良好的评估方法应该能够检测出分割图像中的细微变化。
评估方案通常是根据细分目标确定的。对于特定的应用具有适当的系数对于成功评估至关重要。如果分割的目的是测量神经解剖结构的体积，则体积误差分析可以满足需要。对于分析和系统评估，需要更复杂的方法。 Zhang（1996）将系统评价方法分为两类：分析方法和经验方法。分析方法根据其原理和特性直接检查和分析分割算法，而经验方法则采用间接判断，将分割算法应用于图像测试和测量结果质量。
最近，一些研究人员（Warfield等，2004； Fenster和Chiu，2005； Udupa等，2006）提出了用于表征图像分割算法性能的准确性，精度和效率的报告。准确性是指分割结果与代表真实分割的参考标准进行比较的程度。精度是指应用于相同图像数据的分割的可重复性。效率提供有关算法实际使用的信息，例如计算复杂度和处理时间。
准确性和精确度评估可以大致分为基于距离的系数，基于区域的系数以及整个图像的统计分析（Bland和Altman，1986； Zhang，1996； Chalana和Kim，1997； Cox和Cox，2000； Chang，1996）。 Warfield等，2004； Fenster和Chiu，2005）。为了适应各种评估情况，可以使用与统计推断相关的多个系数，例如，类内相关性。当描绘轮廓时，使用基于距离的系数（例如，Hausdorff距离（Huttenlocher等，1993）），该距离基于分割轮廓（或3-D中的曲面）与真实边界之间的距离的量度。边界至关重要。另一方面，当对象的区域（或体积）的大小和位置测量至关重要且是分割的目标时，将使用基于区域的系数。 Cox和Cox（2000）对各种基于区域的相似系数进行了广泛的研究，其中一些总结在表1中。
在基于空间重叠度量的许多基于区域的系数中，Jaccard（Jaccard，1912）[也称为Tanimoto（Duda和Hart，1973）]和Dice（Dice，1945）系数已被广泛用于分割方法在脑图像中的简单性（Vannier等，1991; Shan等，2002; Dogdas等，2005; Ashburner和Friston，2005; Hernandez和Frangi，2007; Joshi等，2007）（2007年； Sharief等人，2008年）。 Jaccard系数κj度量两组（Ω1和Ω2）的交集面积除以它们的并集面积之比。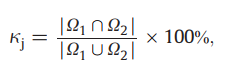

Dice系数κd是通过一种称为kappa统计量的可靠性测度得出的（Zijdenbos等人，1994； Donner和Zou，2002），计算出相交面积的比值除以每个面积的平均值，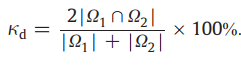

这两个全局测量的性能系数通常与表征对象中正确分割多少像素（或体素）以及多少像素（或体素）的灵敏度和特异性系数有关。正确地分别排除了对象外部。
Zijdenbos等。（1994年）使用Dice相似系数访问人脑中白质病变的定量分析。 Dawant等。（1999年）采用Dice系数定量评估了他们在磁共振（MR）图像中头部内部结构的分割方法。
Shattuck等。（2001年）比较了部分容积组织测量模型，该模型使用Jaccard和Dice系数对非脑组织的白质和灰质进行了分类。 Shan等。（2002年）还使用Jaccard和Dice系数在从互联网脑部分割存储库（IBSR）获得的20个正常MRI数据集上评估了其脑部分割算法（MGH，2007年）。最近，Crum等。（2006年）提出了结合模糊集理论使用Jaccard来评估分割和配准技术。 Udupa等。（2006年）提出了一种框架，该框架通过计算包含Jaccard，Sensitivity和Specificity系数的七个参数的最小集合来评估图像分割算法。 Wu等。（2006）和Kloppel等。（2008年）使用敏感性和特异性系数评估其在多发性硬化病灶和阿尔茨海默氏病（AD）中的MR图像自动分割方法。
鲍威尔等。（2008年）比较了基于Jaccard，Dice和Sensitivity系数的皮质下和小脑大脑结构自动分割算法。
本文介绍了所描述的性能度量系数的内在属性和基本特征，这些系数已被广泛用作许多评估框架中的基本要素。在探究Dice和Jaccard系数的性质及其相互关系的同时，我们还提出了一种新的性能度量系数一致性，用于表征全局误差以及相应的正确分段。从数学上讲，用于评估细分结果的整合系数比Jaccard和Dice系数提供了更大的分数范围。此外，我们提出了用于测量背景像素（或体素）误差的灵敏度系数，而不是特异性系数。将使用多种分割技术来提取和展示这两个新的性能测量系数的优点，以提取各种大脑图像数据集中的解剖和病理结构。
本文的其余部分安排如下。方法部分介绍了新系数的一致性和敏感性的定义。导出并建立了一致性，Jaccard和Dice系数之间的关系。
我们使用各种重叠场景演示了合格性和敏感性系数的典型得分。还展示了Jaccard，Dice，整合，特异性和敏感性系数的内在特性。结果部分通过评估从各种算法在2-D和3-D中的幻影和脑部图像上获得的各种分割结果来说明所提出系数的优点。最后，在“讨论和结论”部分中，讨论了与结果相关的不同性能度量系数的基本特征，并对本文的贡献进行了总结。
方法
一致性
分割结果的定量性能分析非常重要，因为没有一个完美的分割算法可以适用于所有类型的脑部图像，而且通常精度和精度都有限。一种评估算法性能的方法是通过计算机方法测量分割图像与参考图像之间的差异，该参考图像是最佳预期结果（Zhang，1996）。该参考图像（通常称为黄金标准或地面实况）和分割图像是从相同的输入图像中获得的。对于合成图像，可以从图像生成过程轻松获得真实的分割。但是，当处理患者的真实图像或在动物模型中，真相是未知的，通常由专家手动绘制的图像作为参考。根据Fiez等人的研究。（2000年）关于观察者内部和观察者之间的可靠性，人工分割结果在观察者内部和观察者之间产生了高度一致性。
随着使用统计和变分方法的分割技术的最新进展，许多算法提供了分割结果的所谓“子像素”（或“子体素”）估计。不是将每个像素（或体素）标记为属于或不属于区域，即二进制标记{0，1}，而是使用部分关联的表示法。为了适应提供模糊分割结果的方法，我们将模糊分割表示为Ωfs，将模糊基准表示为Ωfr，其部分关联采用连续域[0，1]中的值。模糊参考可以通过平均多个手动轮廓来生成，这些轮廓本质上是二进制的。一种替代方法是使用STAPLE算法（Warfield等人，2004年）从一组专家产生的一组轮廓中估计真实分割的替代物。类似地，可以通过对多次重复的结果求平均，将二进制分割结果转换为模糊分割。
为了简单起见，让我们首先考虑从参考（蓝色实线轮廓）和分段方法（红色虚线轮廓）获得的模糊蒙版的二进制情况，如图1a所示。称为一致性κc的全局相似系数为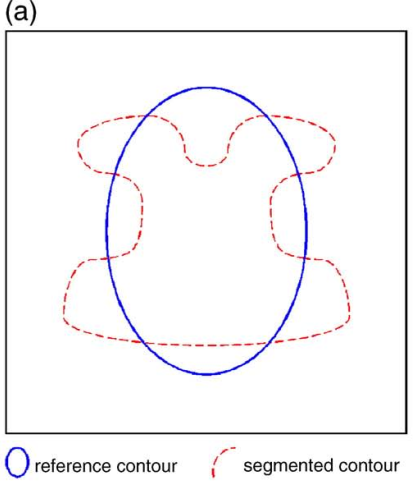

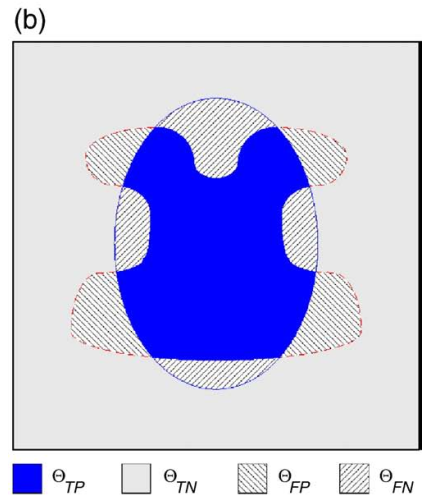
图1.示意图，显示了在计算性能测度系数时模糊区域的定义。（a）模糊分割结果（红色虚线轮廓，Ωfs）叠加在模糊参考标准上（蓝色实线轮廓，Ωfr）。（b）定义ΘTP，ΘTN，ΘFP和ΘFN的模糊区域的定义。

讨论和结论
这项研究的目的是研究基本性能测量系数的内在属性和基本特征，这些系数已被广泛用作评估神经图像分割算法的许多评估框架中的基本要素。同时，我们基于模糊分割Ωfs和模糊参考Ωfr的空间重叠情况，开发了一个全局性能度量系数一致性。可以从测量错位分割区域ΘAE与正确分割的区域ΘTP的比率的角度来解释此新的全局性能度量系数，如等式所示，该比率定义为差异与一致性比率ξ。（3）和（6）。虽然骰子与杰卡德的关系在文献中已有描述（Shattuck等，2001； Crum等，2006），例如等式。（9a）和（9b），它们的性质很少被明确利用，并且它们的绝对值难以解释（Zijdenbos等人，1994）。如图2所示，我们探索了Dice和Jaccard系数相对于ΘAE和ΘTP的得分分布，并建立了Dice，Jaccard和合格性之间的数学关系。
通过评估分割脑部MR图像中的四种不同的计算机化方法来说明“一致性”的优点，如图1和2所示。 10-15。在数学上，一致性的得分范围是基于等式（3）的（-∞，1]，而其他相似性系数则介于0和1之间，请参见表1。与图4一致，我们观察到得分值图示中κc的总值始终小于κj和κd的分数，合格系数的得分范围比Jaccard和Dice系数大得多，尤其是在分割结果较差的情况下。
这可以从图3进行解释，图3表示“一致性”基于ξ具有更好的判别能力。因此，一致性更好地能够检测分割图像中的细微变化。
特异性系数的一个特殊特征是将θTN并入到计算中，如公式1所示。（15）。
因此，当前景和背景结构均对分割目标很重要时，可以在检测和分类应用程序中更适当地使用“特异性”。在提取特定大脑结构的情况下，例如call体，海马体和皮层，与ΘTN相关的背景通常没有意义，对于进一步的分析也没有重要意义。使用受ΘTN约束的特异性来评估此类分割结果可能不灵敏且不准确。
首先，具有不同尺寸的图像中相同的结果具有一致的“一致性”，“ Jaccard”，“骰子”和“灵敏度”值，但特异性得分不同，如图8和表3所示。
对具有不同尺寸的图像中的大量分割结果进行的特异性统计分析可能会因ΘTN而产生额外的差异。此外，“合格性”，“提卡”或“骰子”通常与“敏感性”和“特异性”相关联，以进行更全面的评估。不同的“特异性”值与其他得分一致的绩效指标有冲突。
第二，较差结果的特异性得分可能高于较好结果的得分，例如，图9和表4中所示的各种图像中具有不同尺寸的对象。第三，ηspf得分往往较高。并由于θTN彼此接近，而θTN通常较大，即θTN≫ΘFP时ηspf≈1。因此，评估大图像中的小神经解剖结构并不敏感，因为对特异性的统计分析可能无法提供明显的差异。
我们通过提出一个新的测量系数敏感度来解决此问题，该系数的得分值不依赖于ΘTN。可以通过测量过度分割的区域ΘFP与模糊参考区域Ωfr的比率来解释灵敏度。当ΘFP= 0时，ηsbl的最高分是100％，当ΘFP=Ωfr时，ηsbl的得分为零，而当ΘFPNΩfr时，得分为负。与特异性相比，如图17和表4所示，在评估基于ΘFP的分割算法的性能时，灵敏度提供了更加独特和可靠的评分。此外，有趣的是，当ΘFP=ΘFN时，ηsbl=ηstv=ΘXTPfr [见等式。（14）和（16）]。换句话说，灵敏度和灵敏度的分数均基于Ωfr，当ΘFN和ΘFP相等时，它们是相同的。
尽管Jaccard，Dice和Specificity系数在描述细分算法的性能方面存在差异，但评估分数在统计上相似，但分数范围较窄，如结果部分所示。因此，要严格区分不同的分割算法的性能并不容易，尤其是在结果较差的情况下。出于统计推断的目的，Zou等人。（2004年）提出了使用logit（κd）= ln {κd/（1-κd）}对Dice系数进行logit变换。
此对数变换将κd的域从[0,1]映射到无界范围（-∞，∞），以进行更好的评估。另一方面，拟议系数的一致性和敏感度的域在范围（-∞，1]中固有地不受限制，该范围为解释提供了更高的判别分数值。
综上所述，提出了一种新的全局性能度量系数一致性方法，并阐述了该方法的优点。我们建立了数学关系，并探讨了Conformity，Jaccard和Dice系数之间的内在属性。 Conformity在检测分割图像中的细微变化方面具有更好的判别能力。还提出了一种新的评估系数敏感度，以测量金标准以外的残缺像素（或体素）的误差。与特异性相比，在评估过度分割错误时，敏感性具有一致且可靠的评分，尤其是对于小的神经解剖结构。这项研究为Conformity和敏感性的优劣提供了一些证据，可以将其进一步整合到更复杂的评估框架中，并在各种神经图像处理应用中进行统计和变异分析。