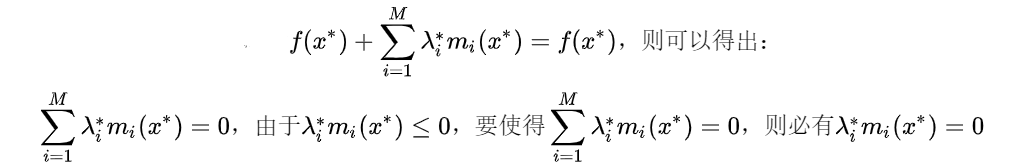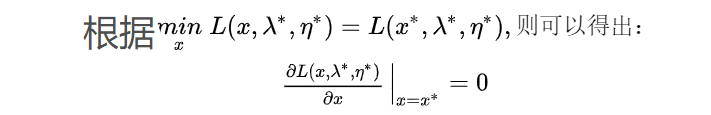一、简介

约束优化问题的原问题（Primal Problem）的一般形式如下：

%5C%5C%0A%26s.t.%5C%20mi(x)%5Cle0%2Ci%3D1%2C2%2C%5Ccdots%2CM%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20n_j(x)%3D0%2Cj%3D1%2C2%2C%5Ccdots%2CN%0A%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0A%0A%26%5Cmin%7Bx%5Cin%5Cmathbb%7BR%5Ep%7D%7Df%28x%29%5C%5C%0A%26s.t.%5C%20m_i%28x%29%5Cle0%2Ci%3D1%2C2%2C%5Ccdots%2CM%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20n_j%28x%29%3D0%2Cj%3D1%2C2%2C%5Ccdots%2CN%0A%0A%5Cend%7Balign%7D%0A&height=67&width=202)

求解约束优化问题需要用到拉格朗日乘子法，定义拉格朗日函数：

然后原问题可以转化为以下优化问题，这两个优化问题具有同样的解：

可以说明一下为什么上述约束优化问题可以求得原问题的最优解：

【当满足原问题的不等式约束的时候， 才能取得最大值，直接等价于原问题，如果不满足原问题的不等式约束，那么最大值就为 ，由于需要取最小值，于是不会取到这个情况。】

也就是说虽然拉格朗日函数对没有约束，但是在求解过程中会过滤掉不符合原问题的约束的。

二、对偶关系证明

原问题的对偶问题为

可以看到原问题是关于的函数，对偶问题是关于的最大化函数。有如下定理：

这个关系可以简单地得到证明：

三、对偶性的几何解释

对于上述约束优化问题，可以写出它的拉格朗日函数：

然后表示出原问题和对偶问题的最优解和：

接着定义集合G：

集合G在二维坐标系下表示的空间假设为下图：

G
因此可以表示为：

在图中可以表示为：

p*
同样地也可以用和来表示：

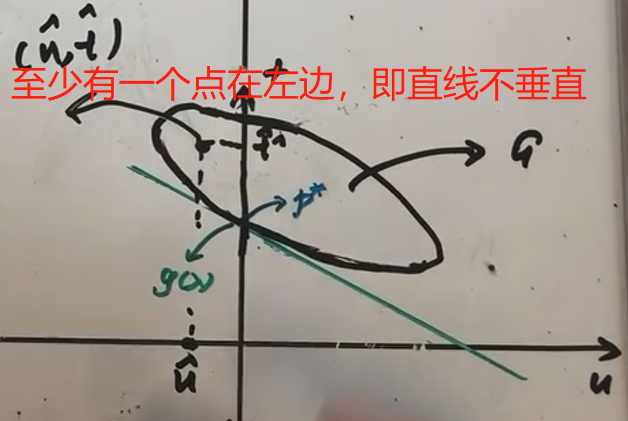
表示以为斜率，以为截距的直线，而即为与区域相切最小截距的直线。如下图所示：

g(λ)
结合上图来看，而也就可以认为是调整斜率使得直线截距最大时的的值。可以想象无论直线怎么变动，所取得的极值都不可能比大，这也就解释了为什么对偶问题最优解总是小于等于原问题最优解。
如果则为弱对偶关系；如果则为强对偶关系。
在某些特殊情况下可以使得强对偶关系成立，在图中表示如下：

强对偶关系
如果一个约束优化问题是凸优化问题且同时满足Slater条件，那么可以使得：

但是并不能推出该约束优化问题是凸优化问题且同时满足Slater条件，这是因为Slater条件是的充分不必要条件，还有其他的条件可以使得约束优化问题满足。

四、Slater条件

Slater条件指的是使得。
指的是定义域除去边界的部分。
有以下两点说明：
①对于大多数凸优化问题，Slater条件是成立的；
②放松的Slater条件：如果 M 个不等式约束中，有 K 个函数为仿射函数，那么只要其余的函数满足 Slater 条件即可。因为在定义域内寻找一个满足所有的点是比较困难的，因此放松的Slater条件会减少一些复杂度。

几何理解：

五、KKT条件

对于原问题：

以及其对偶问题：

如果原问题和对偶问题满足强对偶关系，则原问题和对偶问题具有相同的最优解，另外它们还天然地满足KKT条件（Karush-Kuhn-Tucker条件）。假设原问题最优解对应，对偶问题最优解对应和 ，则KKT条件为：

可以进行以下证明：

为了满足，两个不等式必须成立，于是，对于第二个不等于号需要满足互补松弛条件，即

对于第一个不等于号，需要有梯度为0条件，