主要内容

1. 偏导数
2. 多元复合函数求导法则
3. 方向导数与梯度
4. 多元函数泰勒公式
5. 多元函数的极值
6. 矩阵的求导

偏导数

一阶偏导数

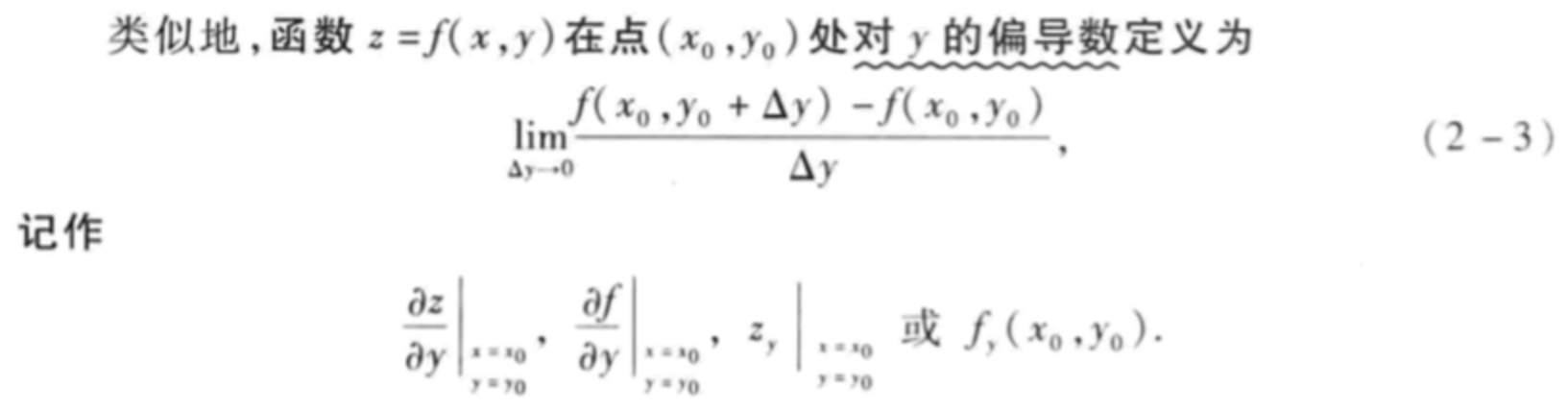
总结**：其实就是对多元函数的某一个变量求导，把其它变量当作常数。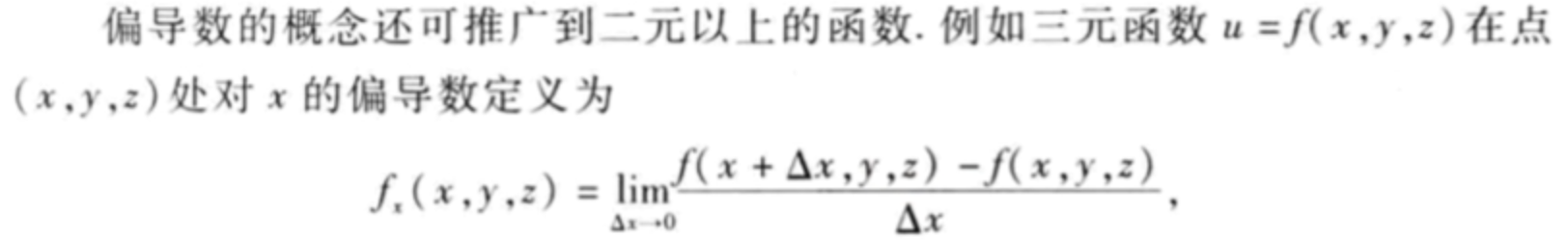

二阶偏导数

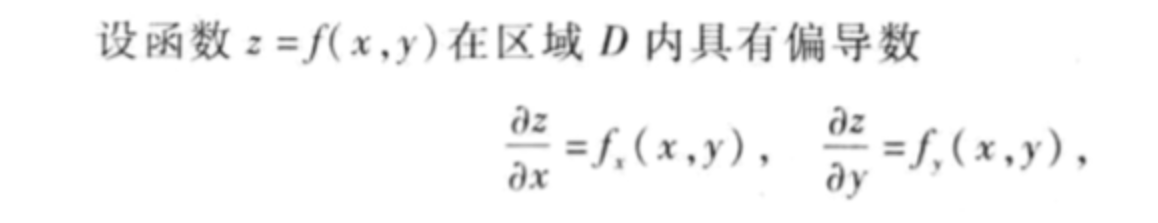
多元复合函数求导法则

总结：一开始根据题目画出链路图，对每条链路上求导并相加。

一元函数与多元函数复合的情形

多元函数与多元函数复合的情形

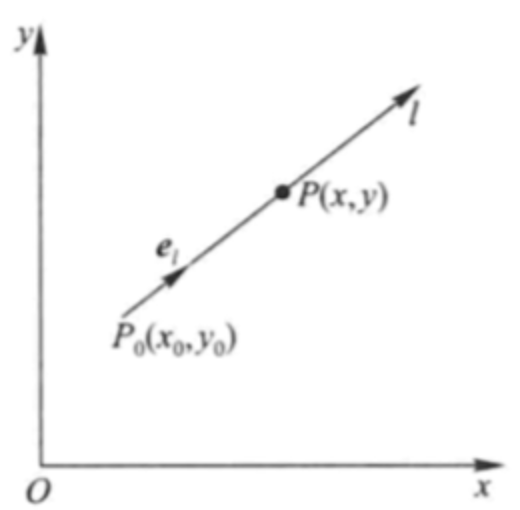
方向导数与梯度（重要）

方向导数

以二元函数为例，将其化作极坐标形式：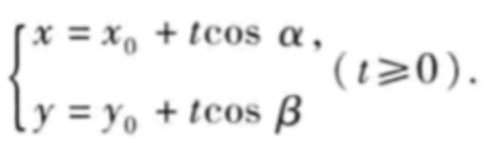

t从图像上看就是从到的距离

引入方向导数（想要求沿着哪个方向走，x和y的变化最大/快）：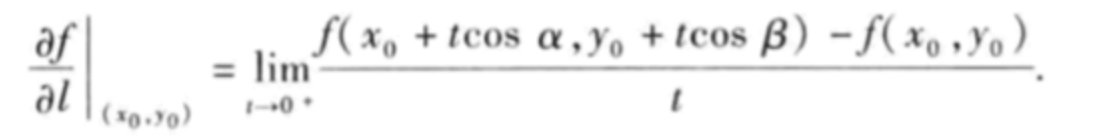
（3）

上式可以转化如下：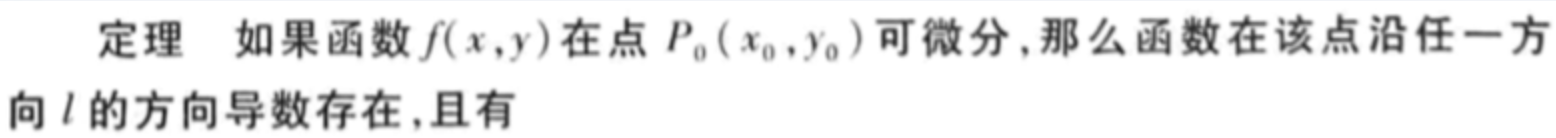

（4）

转化过程如下：

梯度

定义

注意：梯度是向量。

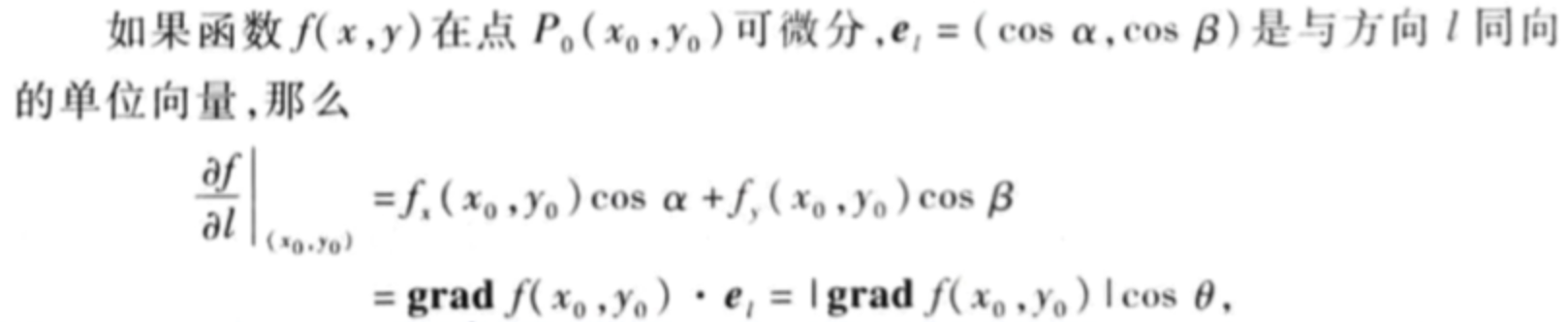
注意：这里的是梯度方向与方向导数方向的夹角。因为，，所以方向导数的区间为，而当方向导数与梯度的方向相同时，即，取得最大值。
总结：方向导数就是梯度与单位向量的点积。沿着**函数梯度方向走可以让函数增长得最快，沿着梯度的负方向**可以让函数下降得最快。



解：
所以在处增加最快的方向就是梯度的方向，将坐标代入得（1，1）。减少最快的方向就是梯度的负方向。
方向导数为：，根据方向导数与梯度方向的夹角代入计算即可。

多元函数泰勒公式

概念

注意实际使用中，一般只用到二阶偏导，即展开的前面三项：


**

Hessian 矩阵（二维或高维）

把上面的二元推广为多元，例如，设函数为，将其泰勒展开至二阶偏导：

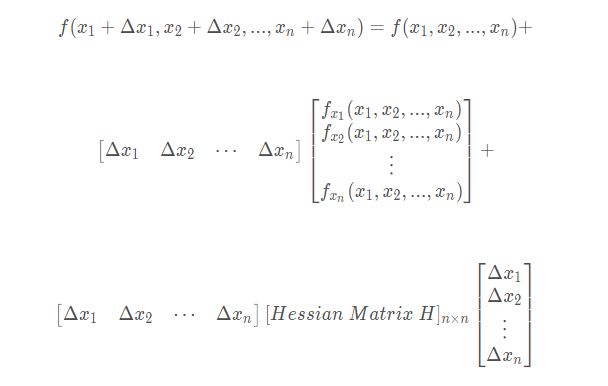
注意：第三行中间Hessian矩阵的通项为：，
举个例子：
总结：

多元函数的极值

必要条件

判断是极值的充分条件

证明：

接下来可以通过判断Hessian矩阵是否是正定矩阵从而判断是否是极值，
因为我们知道正定矩阵M有 ；负定矩阵M有，所以
如果正定，则，那么，则为极小值
如果负定，则，那么，则为极大值
那么接下来就来判断是否为正定：
根据正定矩阵的定理可知，正定矩阵的所有特征值都大于0，负定矩阵所有特征都小于0，
所以求解Hessian矩阵的特征值有：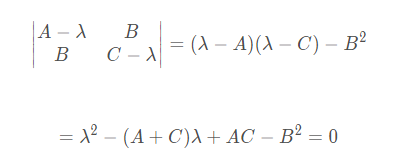

情况1：正定，即,，根据韦达定理有且
情况2：负定，即,，根据韦达定理有且
因为无论正定或负定，都存在极值，所以只要满足即就具有极值。也意味着AC同号。所以
情况1，，所以，此时正定，函数在具有极小值；
情况2，，所以，此时负定，函数在具有极大值。
所以条件（1）得证。
———————————————————————————————————————————————————————

注意：以上是2元函数的判断方法，n元函数就不能只是简单地根据ABC关系。但与上面的推导类似，也是从Hessian矩阵（n阶）是否正定来判断函数是否有极值。
**

矩阵求导

常见性质

1. ，则

1. ，则

1. ，则

1. ，则

总结：对矩阵求导就是对矩阵的每个元素求导，把每个元素搞清楚排起来就是矩阵求导的结果。不过要注意求导后一个矩阵还是一个值。

较复杂性质

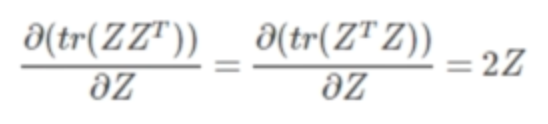
证明：设Z是m*n的，
，就是矩阵Z每一项的平方和，
所以对矩阵每个元素求导有（每个项只有一个特定的），
所以总的矩阵求导就是将其拼起来为

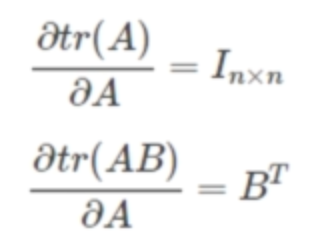
证明：，则
，
所以就是单位阵

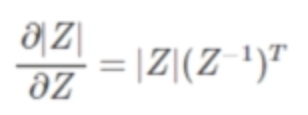
证明：首先根据行列式的性质我们知道所以只有第一项带有。
所以 （将展开后发现就是Z伴随矩阵的转置）。
而，所以