1.2 矩阵的行列式

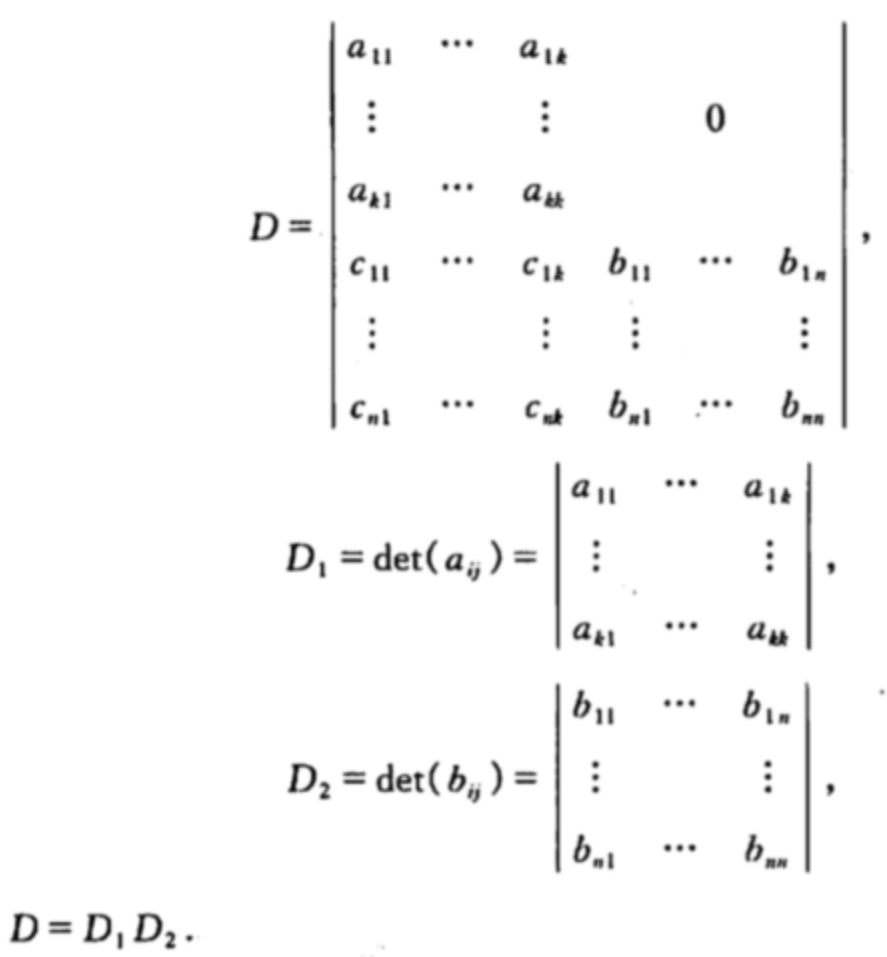
1. 行列式的引入

行列式最早是从解方程组的角度来的**

二阶行列式

先以二阶行列式为例：

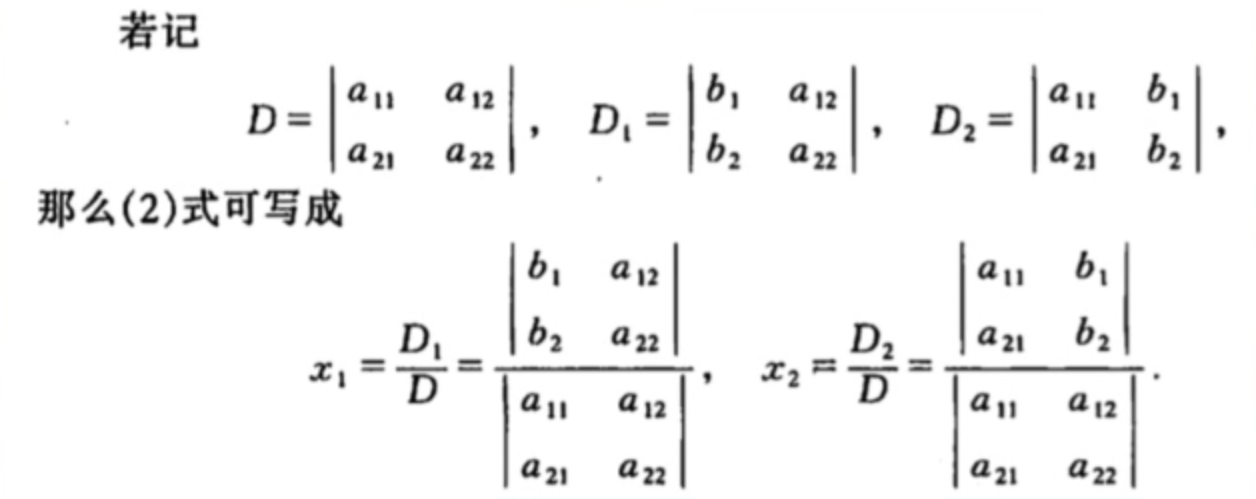
可以发现D就是行列式

三阶行列式

按照此式的定义，三元一次方程组也是满足前面二元一次方程组的行列式表达形式，后面更加通用的克莱姆法则。可以比较快地得到方程的解。但注意用这种方法表示的解时行列式不能为零。

如何计算三阶或更加高阶的行列式

1. 全排列

例：1，2，3的全排列有哪些：
123/132/213/231/312/321，
也就是n个数的全排列有n!种

2. 逆序数

可以先看个例子：

3. 推导过程

由如下的三阶行列式公式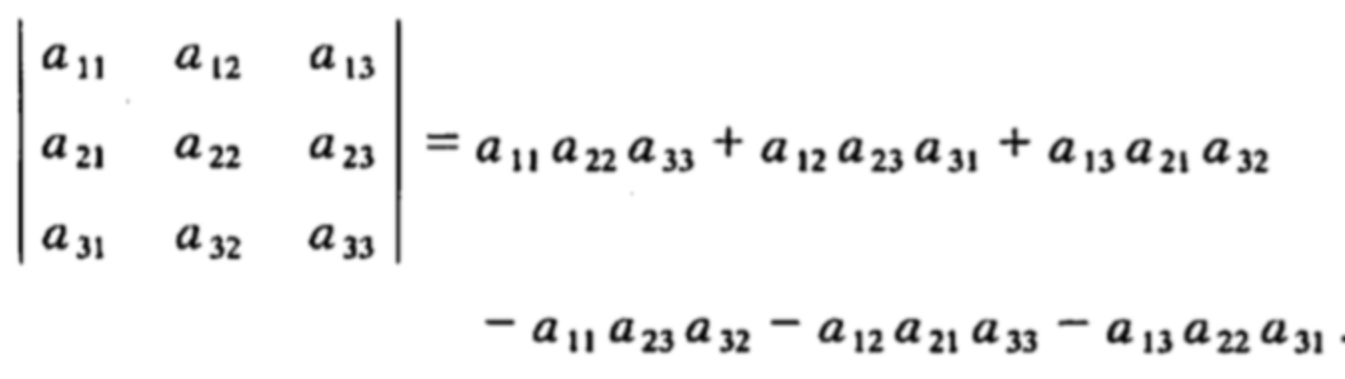

可以看出总共有6项，每项三个的第一个系数都是1，2，3，而第二个系数就是123的全排列，每个项的系数就是全排列的逆序数，如下：
123(t=0)
231(t=2)
312(t=2)
132(t=1)
213(t=1)
321(t=3)
t为各全排列的逆序对，当t为偶数时系数为1，t为奇数时系数为-1。
将系数j记为p，所以三阶行列式的公式可写作：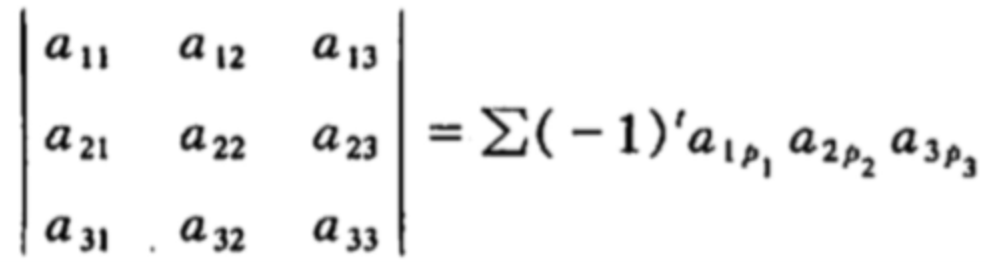
t为各全排列的逆序对

进而可以推导出n阶行列式的计算公式为：
其中，有n!个项。

从而进一步推导：
对主对角矩阵有

对副对角矩阵有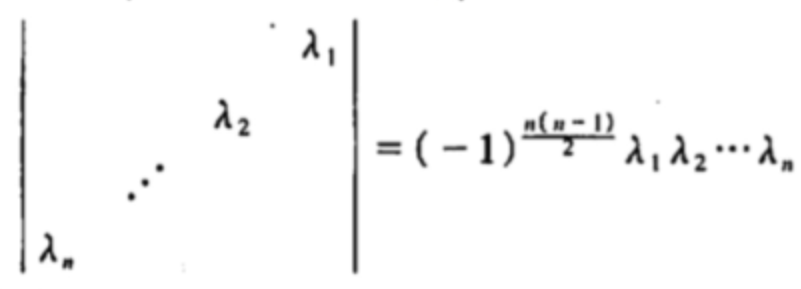

对三角矩阵有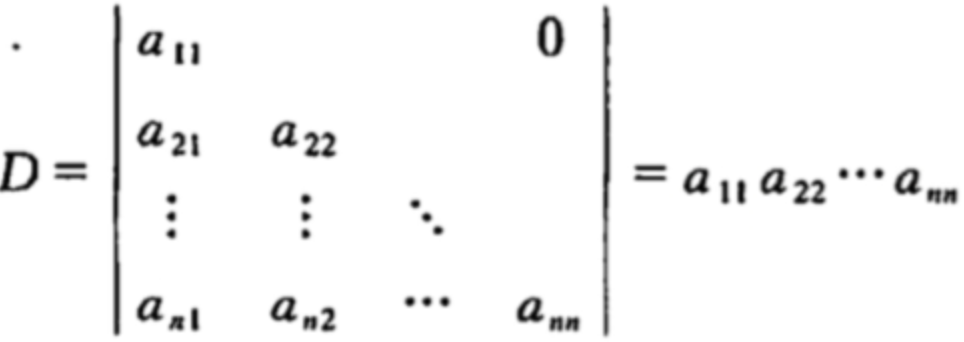

2. 行列式的计算与重要性质

以上两个性质很基础很重要。

证明：如果矩阵A有任意两行（列）完全相同，将这两行（列）交换后的矩阵记为B，则有 |A| = -|B| = -|A|，所以 |A| = 0.

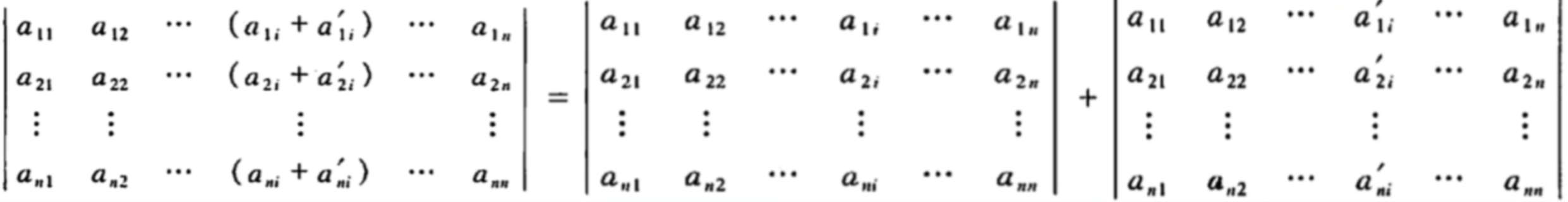
由性质5可推：

用该性质化简行列式可以较快得到行列式值，例如转化成三角矩阵，或发现两行（列）元素成比例等。举个例子

性质8：

3. 行列式按行（列）展开

余子式与代数余子式概念

引理

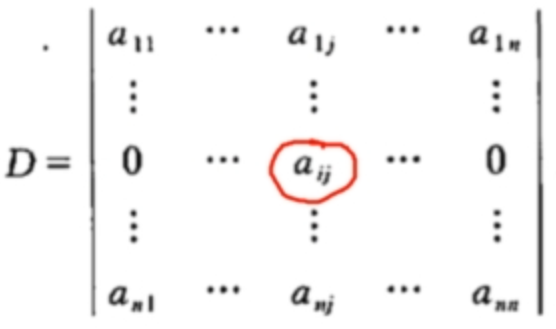
证明：
，由性质8可得，D等于乘以右下角的行列式，符合。

再证明一般情况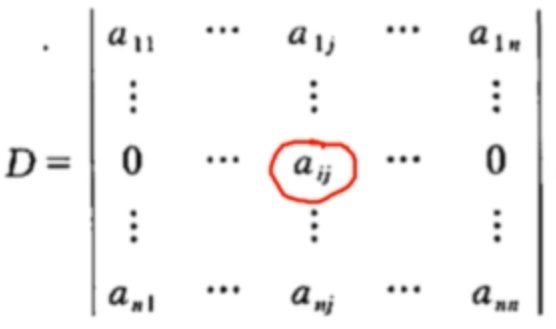

从而引出下述定理（结合上面的性质5）：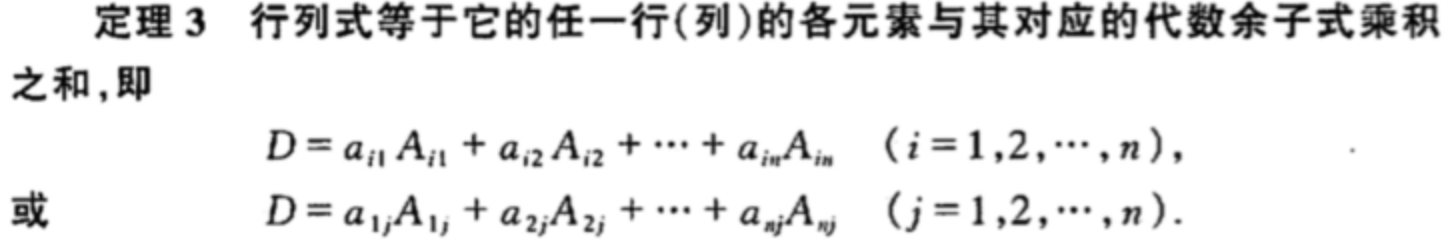

证明如下：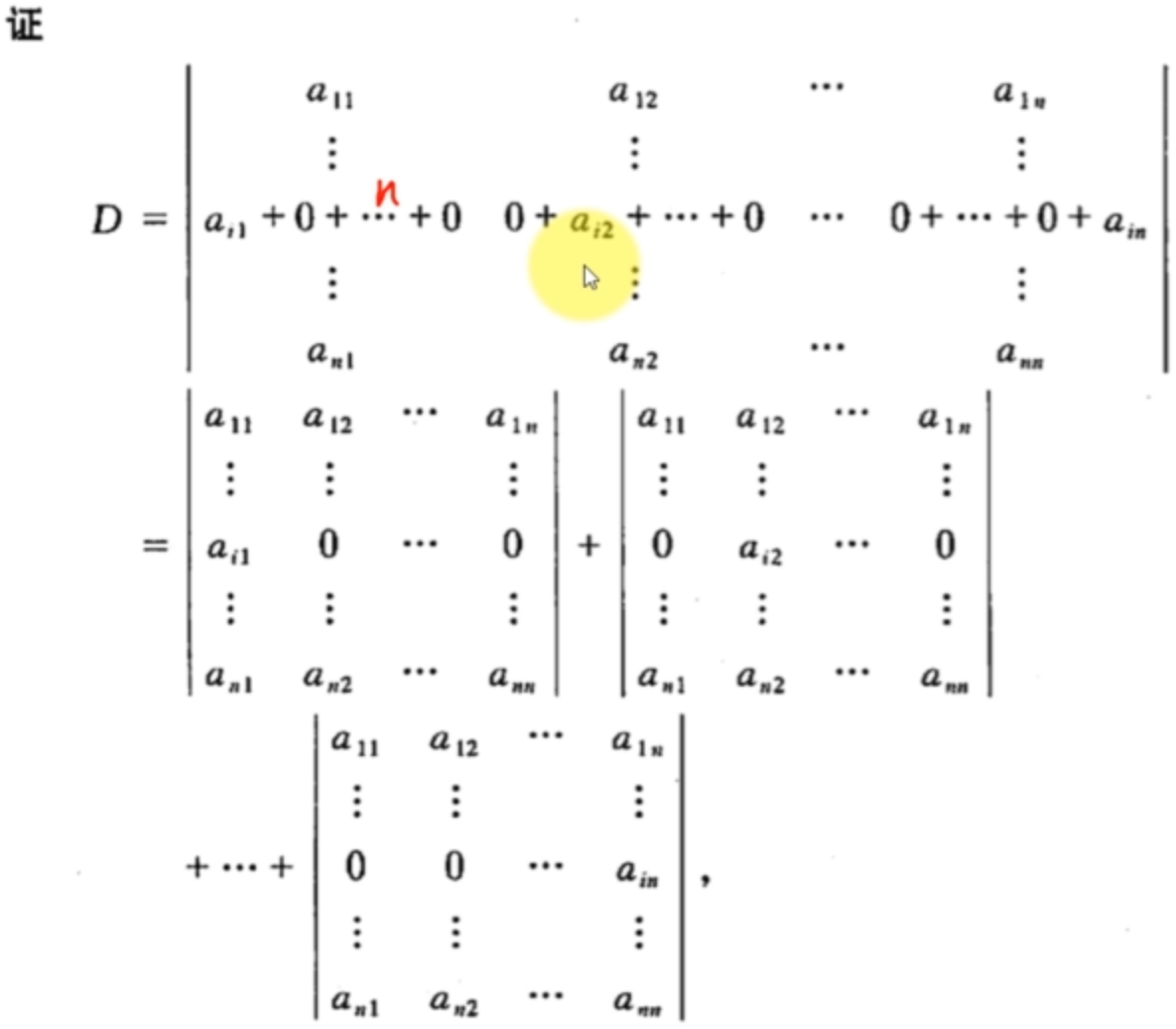

从而可以推出下面定理：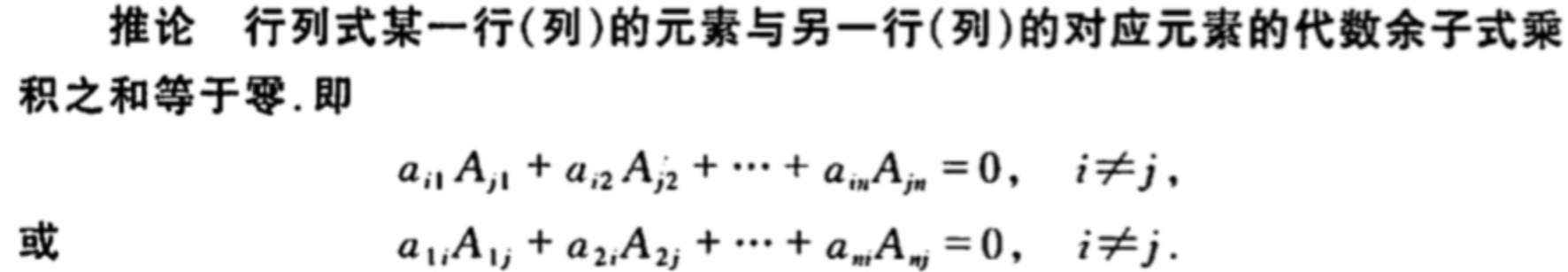

证明如下：右式可以把第j行看作是第i行，所以等式是成立的，因为算余子式时要将该行删去。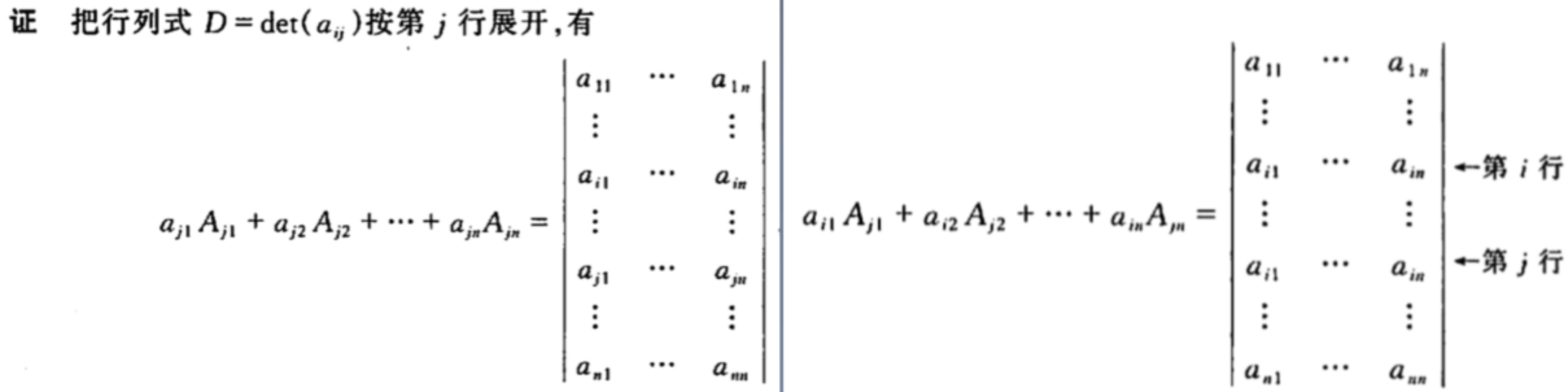

因为右边行列式为0，所以得证。

4. 克莱姆法则

概念

前面其实已经提到

总结两点注意事项：

1. D（系数行列式）不为0；
2. 是将D中第j列的元素用方程组右端的常数项代替后 得到的n阶行列式。

定理

定理4

定理5

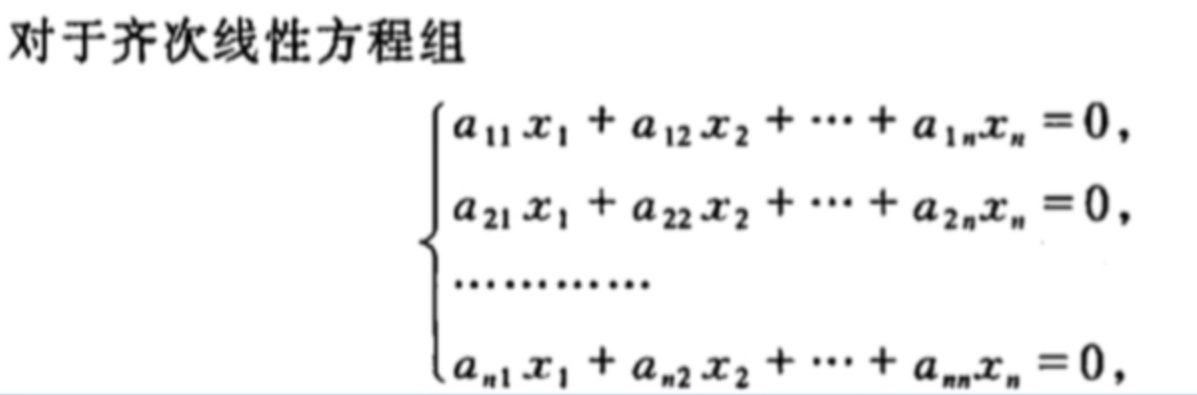
证明：因为齐次线性方程组必有一组解是，又由定理4得，当时，方程组有唯一解，所以该齐次线性方程组只有这一组全为0的解，即没有非零解。

定理5的逆否命题：