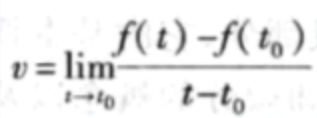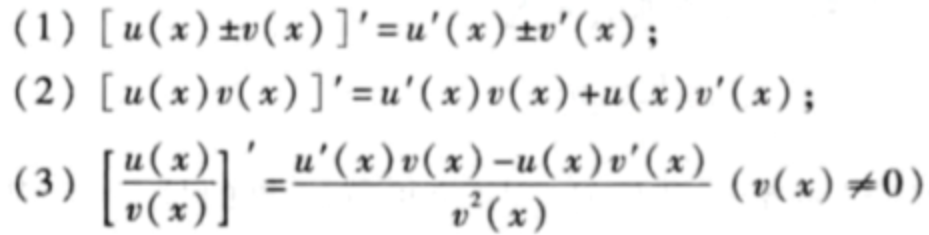2.1 导数中的中值定理

导数

引入

直线运动瞬时速度的角度

曲线切线的角度

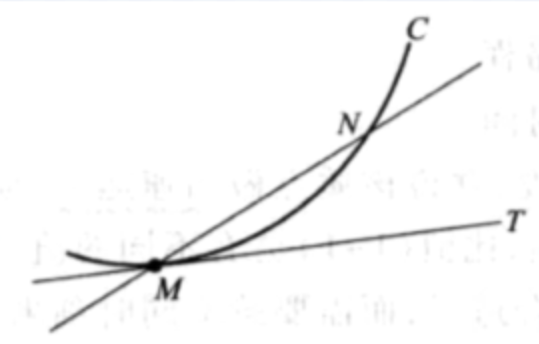
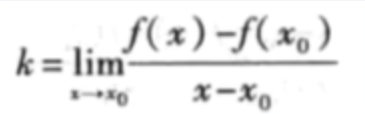
定义

常用函数的导数

定理：导数存在 等价于 左右导数存在且相等
例题：函数f(x)=∣x∣在x=0处的导数。不存在
解：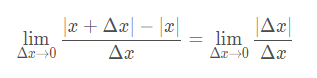
当（右极限或叫右导数），；
当（右极限或叫右导数），；
因为左右极限不相等，故导数不存在。

求导法则

初等变换

复合函数（链式法则）

高阶导数

中值定理

拉格朗日中值定理

从几何的角度理解，就是a，b两点间的曲线上，总是可以找到一个点的切线的斜率与线ab的斜率相等（二者平行）

柯西中值定理

拉格朗日中值定理其实是柯西中值定理的一种特殊情况：将F(x)看作y=x，代入公式发现得到拉格朗日的公式。

洛必达法则

使用情况

已知，求

方法

即分子分母分别求导后再求极限。

证明

首先因为，所以 根据柯西中值定理转换为：
因为，所以当，有，所以，这里只是符号所以可以替换 为x，那么就有. 证毕。