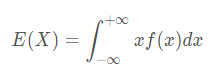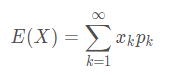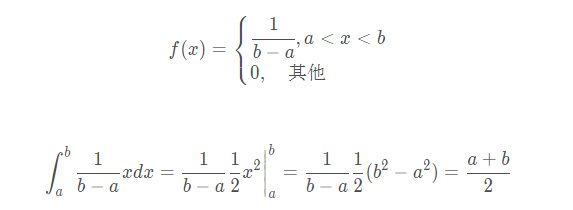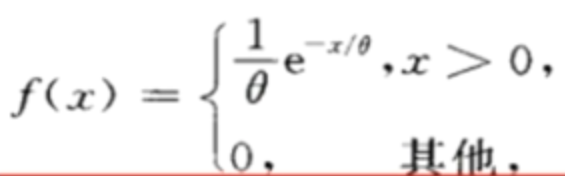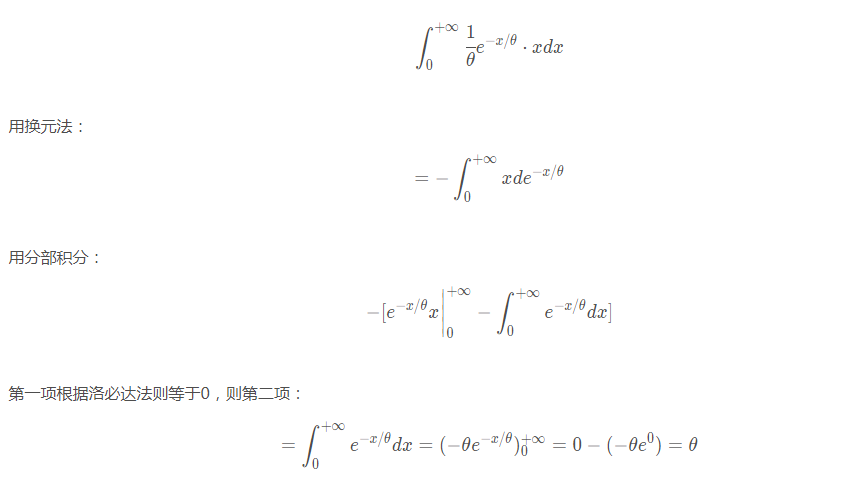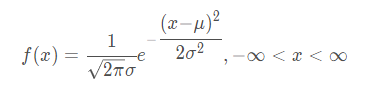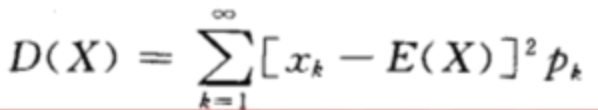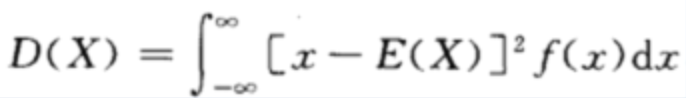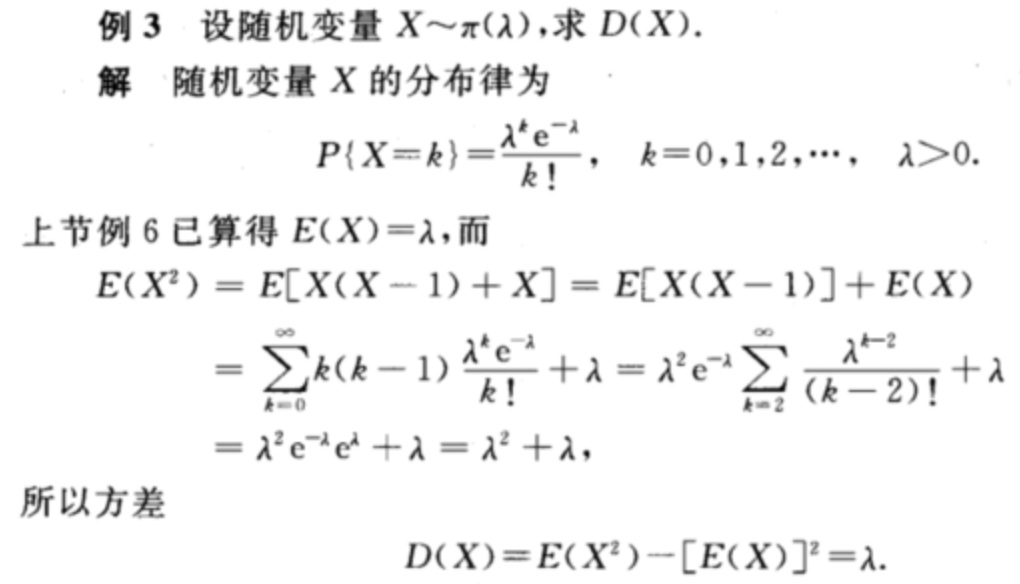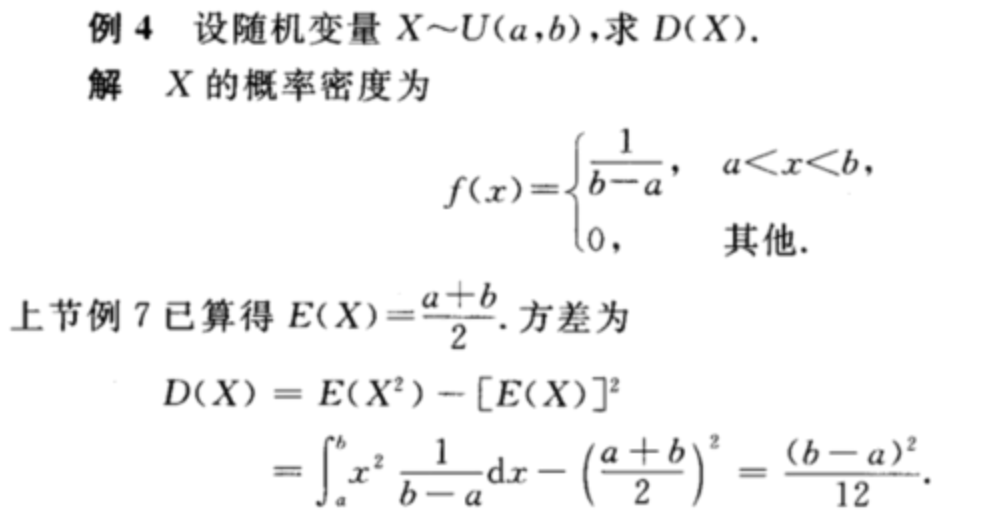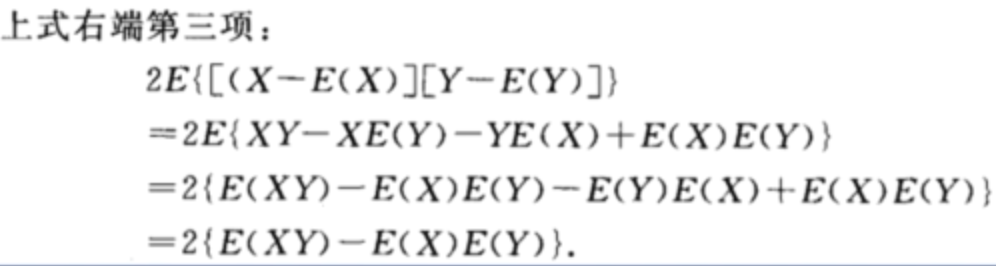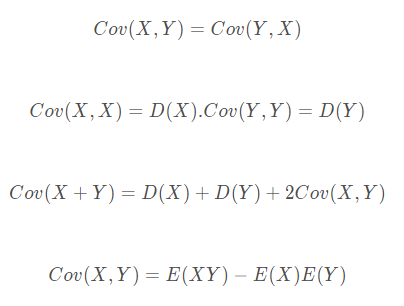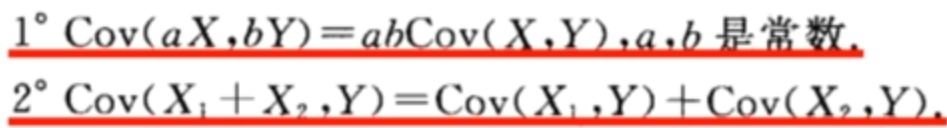掌握目标
1、掌握期望和方差的意义,以及常用离散或连续分布期望方差的计算
2、掌握期望和方差的性质
3、掌握协方差,相关系数,协方差矩阵
期望与方差
期望
连续型(积分)
离散型(求和)
典型概率密度函数的期望
均匀分布
指数分布
高斯分布
典型离散型随机分布的期望
0-1分布
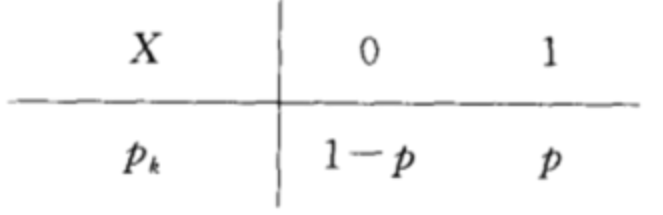
根据定义求期望:
伯努利分布(二项分布)
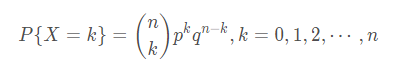
根据定义求期望: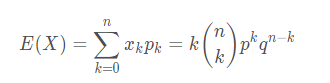
其中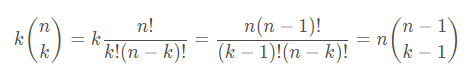
所以
泊松分布

根据定义求期望公式为: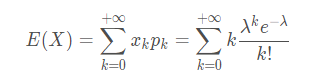
由于k=0时的项为0,所以可以看作从1开始累加: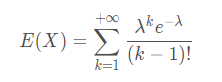

期望的性质
方差
定义

对求数学期望:

方差简单来说就是每一个样本到期望的距离的数学期望。
离散型
连续型
方差的计算
通过上面的方差计算公式,我们发现如果要计算方差还要计算期望再算每个样本的距离很麻烦。
因此下面我们来简化一下方差的计算方法:
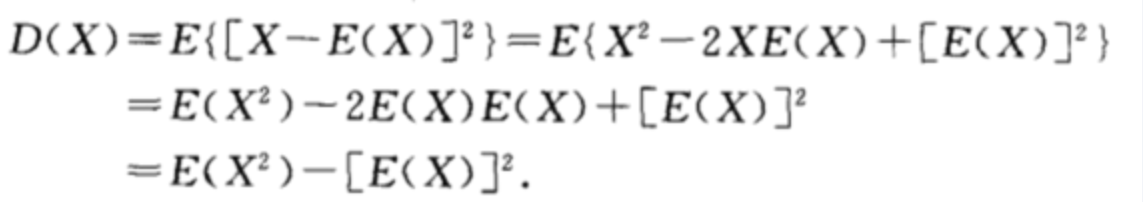
也就意味着要计算方差只要算出上面两项即可。
其中对离散型:,对连续型:
。
常见分布的方差
泊松分布
均匀分布
指数分布

高斯分布
方差常用性质

协方差
引入
在证明方差性质3的时候,我们已经看到,如果两个随机变量X和Y是相互独立的,则
这意味着时,X与Y不相互独立,而是存在着一定的关系的。
协方差和相关系数

由柯西不等式:
所以相关系数是小于等于1的,当相关系数的绝对值等于1时,XY相关性最强;当相关系数为0时,XY相互独立
协方差常用公式
协方差常用性质
相关系数定理
协方差矩阵

推广到n维:
n维正态随机变量的概率密度