信息量

信息量可以直觉理解成一个随机事件x不确定性的程度。
即当发生概率越小的事件发生了，带来的信息量越大；当发生概率越大的事件发生了，带来的信息量越小。
所以信息量与事件发生的概率有关，也被称为随机变量x的自信息(self-information)，描述的是随机变量的某个事件发生所带来的信息量

用数学公式描述如下：
假设X是一个离散型随机变量，其取值集合为，概率分布函数，则定义事件的信息量为：

由于，所以信息量的分布如下图：

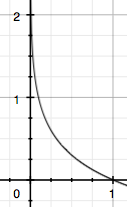
该函数既保证了信息的非负性，又保证了低概率事件含有更高的信息

信息熵

信息熵可以直觉理解成一个概率分布的复杂程度（不确定性）。

数学公式上信息熵是 所有可能发生的随机事件产生的信息量的期望。

即对于某个随机分布，可能有多种可能性发生，每种可能性发生有一个概率，这样我们就可以计算出每个事件的信息量，以及该随机分布的信息熵。

当随机分布的取值个数越多，状态数就越多，概率分布就越复杂，对应的信息熵就越大。
例如当n维离散型随机变量为（其它取值的概率均为0）时，信息熵最小；
当n维离散型随机变量为（均匀分布）时，信息熵最大
所以

相对熵（KL 散度）

相对熵也称为KL散度(Kullback–Leibler divergence)，可以用来衡量两个概率分布的差异。

可以直觉理解为用分布P来描述目标问题，而不使用Q来描述目标问题，得到的信息增量。

数学公式上：
假设一个随机变量X有两个独立的概率分布，则P对Q的KL散度为：

三个性质：

1. 如果两个分布相同，那么KL散度为0
2. 不对称性，即
3. 非负性，即

JS散度

JS散度(Jensen Shannon divergence)是基于KL散度，并解决了其非对称性的问题：

JS散度可以直觉理解为：我们求得两个分布的一个平均分布，然后分别求它到两个分布的KL散度，最后求个平均。所以JS散度是对称性的。

性质：
当两个分布完全没有重叠部分时，JS散度一直为常数1.