1.6 矩阵的特征值和特征向量

向量的内积和范数

向量的内积以及正交性

内积的定义

内积有时候也记为
注意： .
**

内积的性质

柯西不等式

由上述内积性质可以推导出柯西不等式：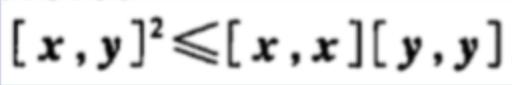

推导过程如下：

由以上性质加上我们中学在二维空间里面向量夹角的概念，即，我们可以推广到高维空间，也可以用来衡量高维空间中两个样本的相似度的一种度量（不同于欧式距离）。

因为在高维空间，模长可以由内积公式诱导出：，. 所以现在在高维空间任意两个向量之间的夹角也有了度量，从高中的二维空间进行了推广。而且可以验证这样的定义是自洽的：
首先我们知道，而上述的，
由柯西不等式可得：，即

范数

线性无关

线性无关的定义：
在向量空间V的一组向量A:，如果存在不全为零的数，使得：

则称向量组A是线性相关的；否则若，称A是线性无关的。
由此定义看出：是否线性无关，就看是否存在一组全为零的使得上式成立。
简单来说，线性相关就是可以用其它的表示。
因此现在我们又可以推导出：A可逆 等价于 等价于 R(A)=n 等价于 线性无关
上面，为列向量。
因为： 若线性相关，则可以被其它表示，那么该列向量就可以被消为零向量，那么 . 所以 等价于线性无关。
同理为行向量时一样可以得证。

正交

概念：

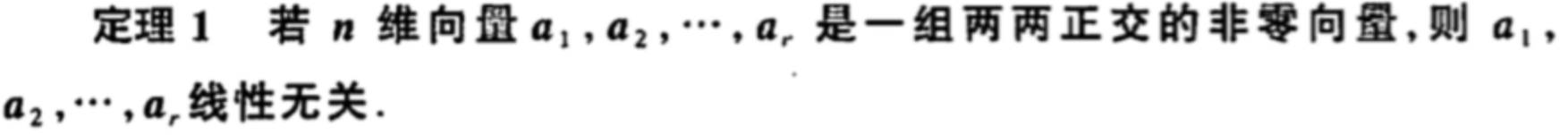
证明定理1：
欲证明线性无关，就是假设，证明：。对上面的方程左右同时点积，因为两两正交，则有. 又因为是非零向量，所以，所以. 同理点积可以证明，所以得证。

规范正交基

思考：如何求出这些表示的系数?
方法：若想求，则两边点积，等式变为，所以

正交矩阵

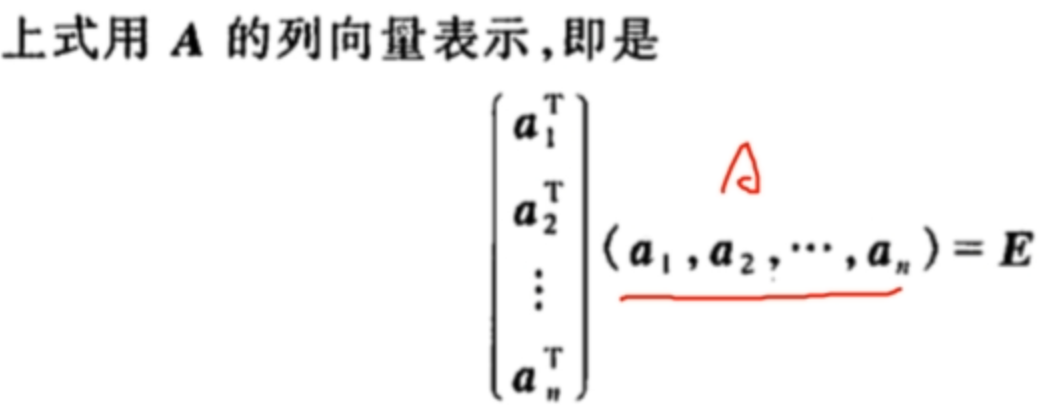
简单来说，A若是正交矩阵，则列向量都是规范正交的，即可以作为规范正交基。

证明上述等价：
，所以，所以A可逆，所以，所以.

方阵的特征值与特征向量

概念

简单来说，就是寻找一个特殊的向量x，对它进行一个矩阵A的变换后，得到的方向跟原先保持不变（平行）。我们就把这种特殊的向量叫做特征向量，这就是其来源。

有时候我们就会给定矩阵A，要寻找一个经过A变换后保持方向不变的向量x。
就可以通过下面的公式计算得到x：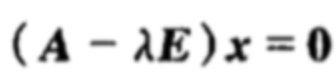

因为A是n阶矩阵，所以也是n阶矩阵，所以根据克莱姆法则，想要求出x的非零解，就有（也可以通过上一章更广泛的定义来推导），所以就转换为：

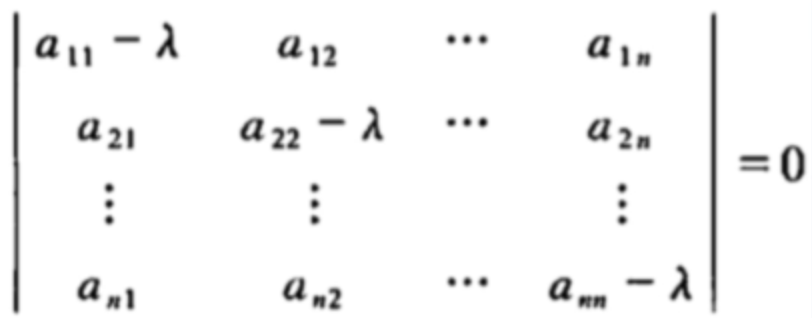
通过上面方程可以求出的值，然后代入原方程求出对应于特征值的特征向量

有时一个特征值会对应多个特征向量。

一些性质：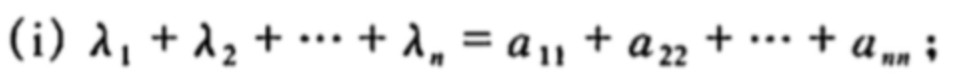

求解出特征值的和与原矩阵的迹相等。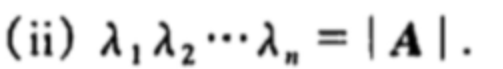

求解出特征值的乘积与原矩阵的行列式。

证明：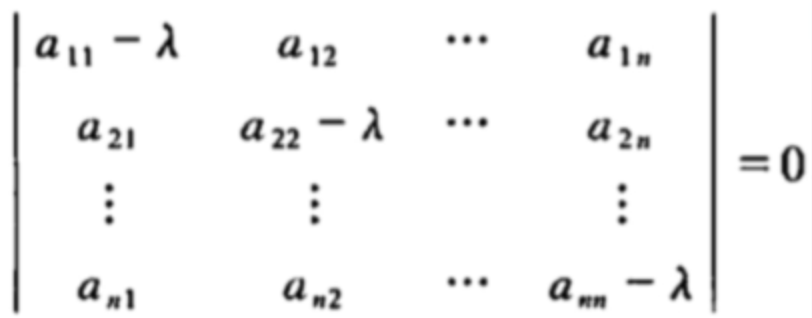
行列式可以化为这样的多项式，
然后可以通过韦达定理证明。

例子

举个例子帮助上面定义的理解：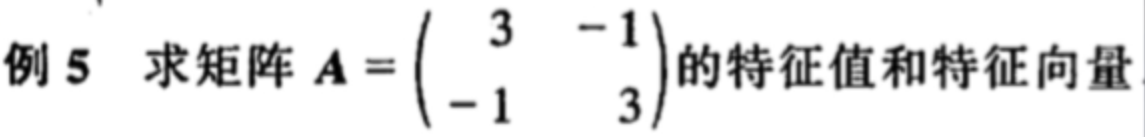

因为求解特征值出现重根，所以解出两个特征向量。

证明（1）：
，那么对就有，那么对就有,即是的特征值；
证明（2）：
，因为A可逆，就有：，即. 所以是的特征值；
同理可以证得是的特征值。

举个例子辅助理解上面的推导：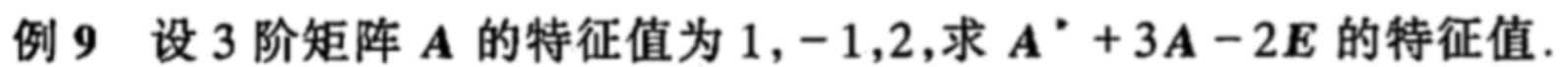

解：
所以由上面的推导 是的特征值。
所以将1,-1,2分别代入计算得到2，-4，8.