等式约束：拉格朗日乘子

推导

经典拉格朗日乘子法是下面的优化问题（注：x是一个向量）：

等式约束：

先引入等高线的概念，以二维函数f(x,y)为例，用平行于XOY的平面去切这个二维函数然后投影至XOY平面上，就可以得到等高线（等高线上函数值相等），越往中心越接近函数最小值。然而这里还有等式约束，也就是要在曲线上找到一个距离等高线中心最近的点。所以很自然地就是要找到等高线与曲线相切的点。因为切线方向是共线的，所以法线方向也是共线的。

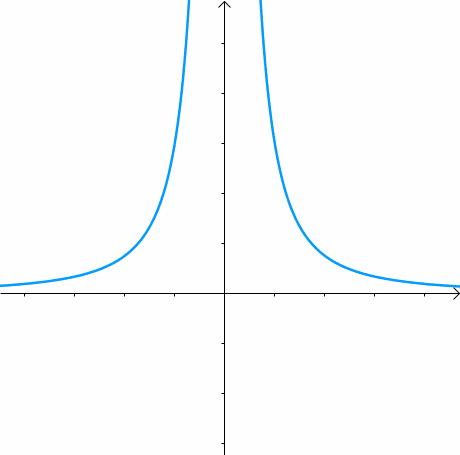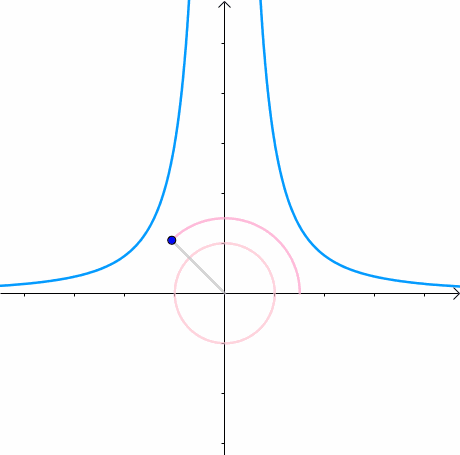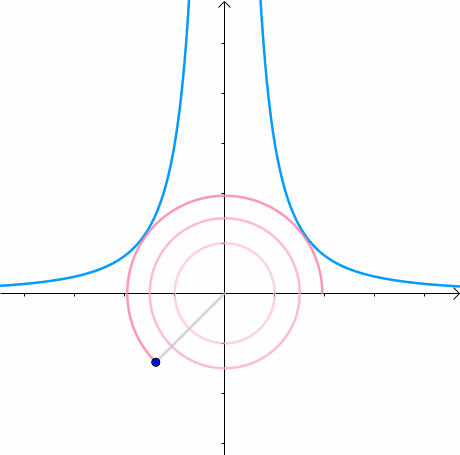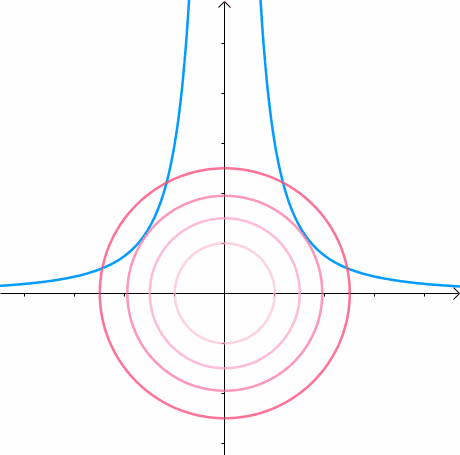
下面来求此时等高线的法线：
设二维函数为z=f(x,y)，那么当高度z为常数c时的等高线也就是：

对其求偏导，并令其等于0有：

可以转化为：

而该函数的梯度可以用各个偏导排列组成的向量表示，即，梯度方向为：
用切向乘以梯度方向有：

所以梯度方向与切线方向垂直，即梯度方向与法线方向共线。即：

也就是此时二维函数与约束函数的梯度方向共线。

以上是二维函数的例子，推广到n维就是：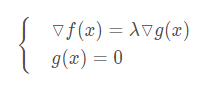

其中
把第一个式子展开有：

即

这里为了统一上面两个方程，我们引入拉格朗日函数：

对拉格朗日函数求导就能得到上面的两个函数。这就是拉格朗日函数的推导。

不等式约束

这里跟等式约束差不多，只是约束函数变为（大于等于可以转化为小于等于）。
首先我们假设等高线中心不在约束范围内，否则最小值就可以直接取中心了。
所以此时f(x)的梯度方向与g(x)的梯度方向是相反的。
那么这时引入的拉格朗日函数为：

上面多引入第二个方程的含义是，当取到的内部点时（即不在曲线g(x)=0上），那么该方程就会得到，那么方程就不起作用了。该方程只有在时使得。该方程有时也叫做KKT条件。

求解流程

下面总结一下求解流程：
假设是定义在上的连续可微函数，最优化问题为：



所以引入的拉格朗日函数为：

需要满足：

从而解出

举个例子辅助理解
解得：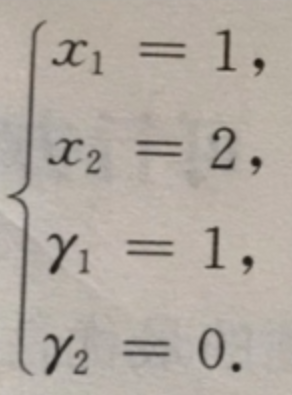

优化的对偶理论

原始问题

注意上式中把x看作一个给定的常数，要寻找得到最大值为，所以这是x的函数。

要求需要分三种情况讨论：
情况一，x满足原始条件的约束，则拉格朗日函数变为：

因为，所以当时，函数取到最大值，即：

所以

情况二，存在使得，那么我们令除了以外的都为0，令所有也都为0（这里是为了找到
而取的），则拉格朗日函数函数变为：

因为，而是给定不变的，所以整个函数没有上界。
情况三，存在使得，那么我们令除了以外的都为0，令所有也都为0，则拉格朗日函数为：

则也是没有上界的，而是给定不变的，所以整个函数没有上界。

对以上三种情况总结，则有：

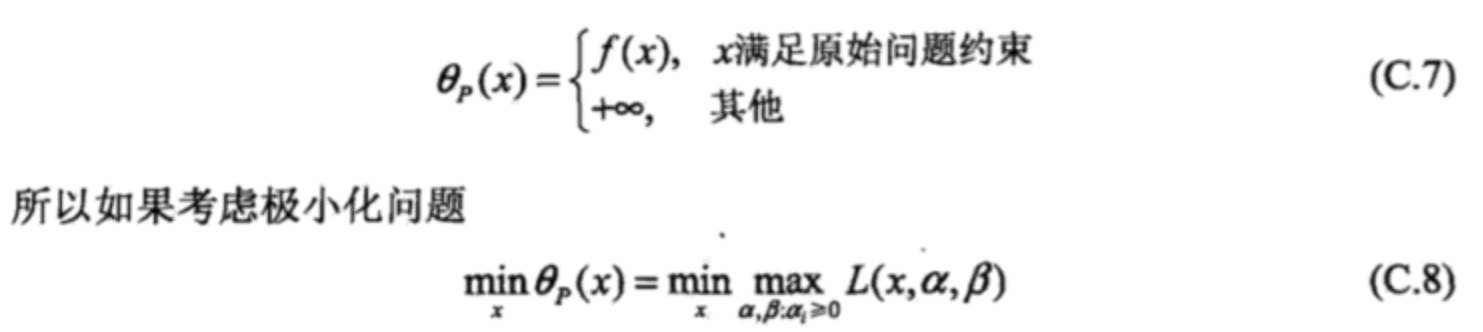
而上式又可以转化为：
，x满足原始问题约束
而这个又是原问题！所以我们知道原问题与是等价的。
所以我们可以将原问题转化求，因为此时我们不用考虑原问题的一堆约束，只要满足
.

对偶问题

弱对偶定理

以上这种形式是弱对偶形式，如果能把不等号变成等号，那么就变成强对偶形式。
变成强对偶形式是有好处的，这样原问题就可以转变为对偶问题来求解，因为对偶问题更容易计算。
下面就来看看什么时候可以取为等号，变成强对偶。

强对偶定理

弱对偶转为强对偶的条件

其中仿射函数就是一次线性函数。
机器学习中SVM算法就都满足上面的条件，所以它可以转化为对偶问题求解。

KKT条件

然而要想对偶问题的解就是原始问题的解，则还要满足以下的KKT条件