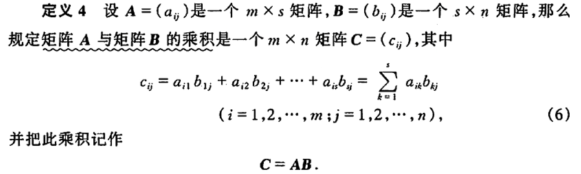1.矩阵的基本概念以及意义

矩阵

image.png

方阵

m=n

行向量

m=1

列向量

n=1

两个矩阵相等

两个矩阵的每一个对应位置上的元素都相等

零矩阵O

所有元素都是0

特殊矩阵

单位矩阵E：对角线上都为1，其他位置都为0的方阵
对角矩阵：是一个主对角线之外的元素皆为0的方阵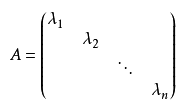
1.1 矩阵及其运算合集 - 图2通常记为：1.1 矩阵及其运算合集 - 图3

2.矩阵的基本运算（加，减，乘）

加法

矩阵加法要注意两个矩阵大小要一样（同型矩阵）
image.png

乘法（数乘矩阵）

矩阵乘法经常用到，要注意两个矩阵的shape，第一个矩阵的列数和第二个矩阵的行数要相等。
image.png

乘法（矩阵乘矩阵）

image.png

矩阵乘矩阵不满足交换律**
image.png

3.矩阵（方阵）的迹trace

只有方阵才有迹
计算公式为：1.1 矩阵及其运算合集 - 图8，即方阵A的迹为主对角线的元素之和
虽然1.1 矩阵及其运算合集 - 图9，但是1.1 矩阵及其运算合集 - 图10.证明如下：
1.1 矩阵及其运算合集 - 图11
1.1 矩阵及其运算合集 - 图12,将该式的i,j符号调换后就是1.1 矩阵及其运算合集 - 图13，所以得证。

4.矩阵的转置

image.png
image.png

总结：**

5.对称矩阵（方阵）

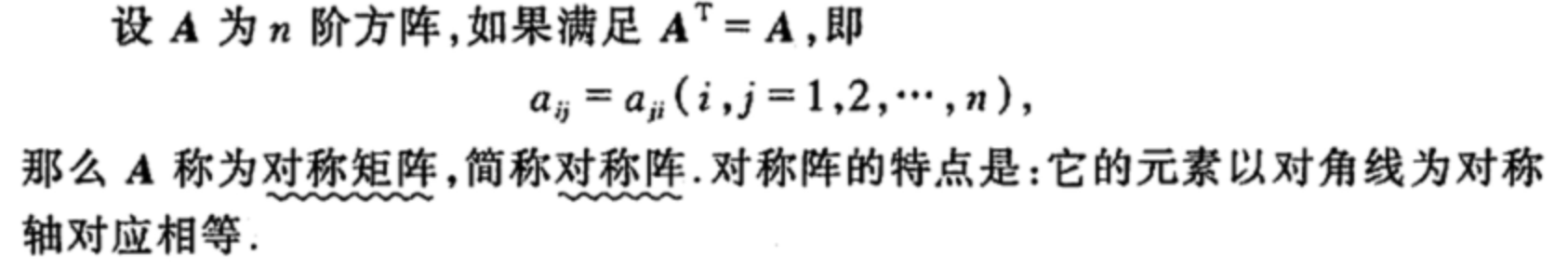
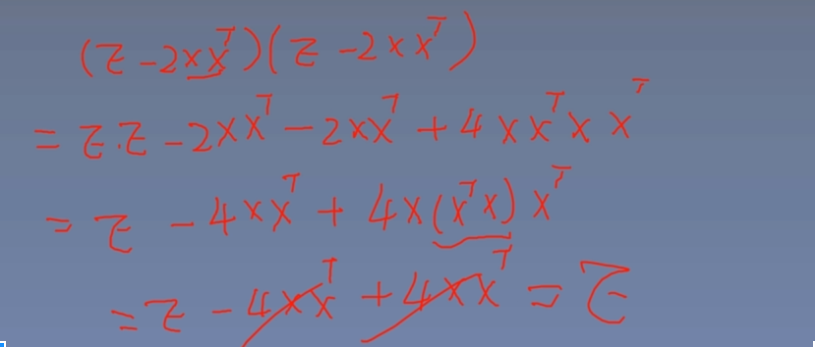
image.png
image.png
image.png
当x、y均为列向量时，1.1 矩阵及其运算合集 - 图19，证明如下：
首先易得1.1 矩阵及其运算合集 - 图20均为实数，则1.1 矩阵及其运算合集 - 图21