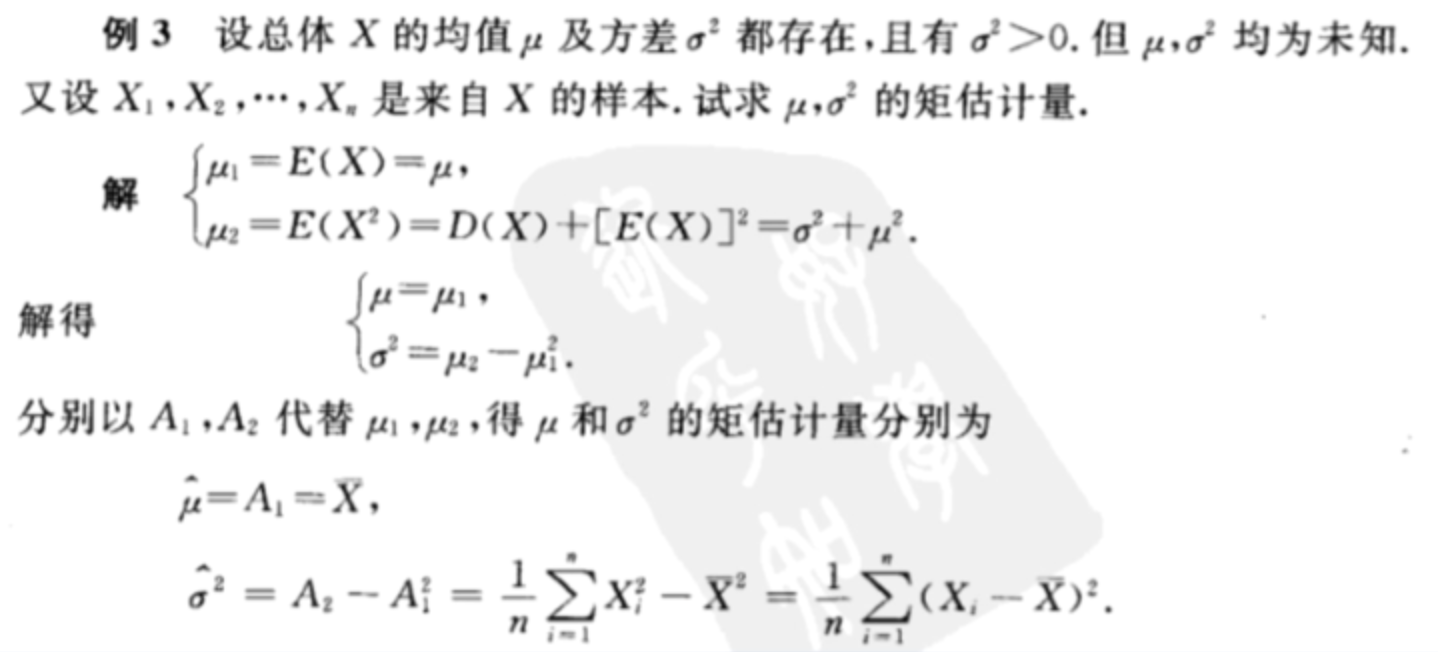主要内容

1. 矩估计
2. 极大似然估计

矩估计

K阶矩

矩估计就是算一些矩的统计量，前面算的期望实际上是一阶矩统计量：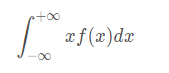

实际是二阶矩统计量：

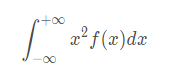
下面看k阶矩统计的定义：

k阶矩中，x都被积分积掉，或者求和求掉，所以这k阶矩的都是关于参数的函数。
注意：上面k阶矩是从概率密度函数来算出来的，得到的都是关于的估计。

样本矩

我们要估计参数就需要有样本，假设现在有样本，则根据样本计算的样本矩定义如下：

一阶样本矩：

二阶样本矩：

阶样本矩：

然后我们要根据样本矩来估计上面中的参数，所以就假设样本矩等于k阶矩：

样本矩是可以通过样本抽样计算出来的，右边就是关于的表达式。
这样就建立了个方程，如果有k个参数，就令，就可以把参数都解出来。

举个例子辅助理解：

极大似然估计

假设是来自X的样本，且是相互独立的。
则联合概率分布可以写成：
离散型可以写作：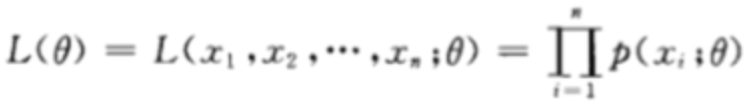

连续型可以写作：

上面等式的右边就可以通过抽取样本并计算抽取出该样本的概率来得到。
这里假设从样本中抽出n个，那么我们认为这n个样本出现的概率是前n大的，因为我们抽的是这n个而不是其它
那么右边抽取n个样本的概率相乘得到的就是的最大值，该式子也称作似然函数。
极大似然估计就是求参数使得的得到最大值。
要求最大值可以转化为求，由于

1. 是很多概率相乘，当样本很多时相乘的结果会很小，从而导致计算机“下溢出”
2. 是连乘的形式不好求导，

因此左右同取对数转化为：

举个例子辅助计算过程的理解：
0-1分布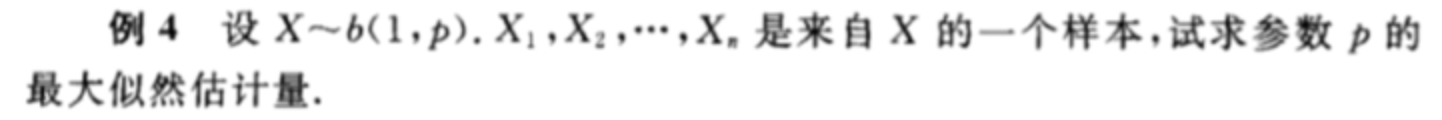





正态分布


均匀分布（较特殊）