主要内容

  1. 随机试验，样本空间，随机事件
  2. 概率定义
  3. 条件概率与乘法公式
  4. 全概率公式与贝叶斯公式
  5. 独立性

随机试验，样本空间，随机事件

随机试验

  1. 扔硬币

image.png

  1. 投色子

    样本空间

    随机试验E的所有可能结果构成的集合称为E的样本空间
    对应上面四个随机试验的样本空间：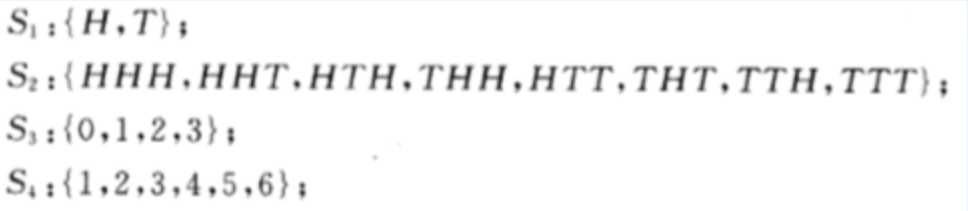
    image.png

    随机事件

    试验E的样本空间S的任意一个子集称为E的随机事件，简称事件
    必然事件和不可能事件
    互斥事件和对立事件（A发生，B一定不发生；A不发生，B一定发生。即P(A)+P(B)=1）

概率

定义

image.png

例题
image.png

条件概率

定义 设A，B是两个事件，且P(A)>0，称3.1 概率基础 - 图5为在事件A发生的条件下事件B发生的条件概率。
例题
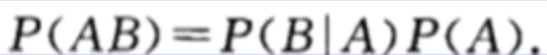
image.png

乘法公式

性质
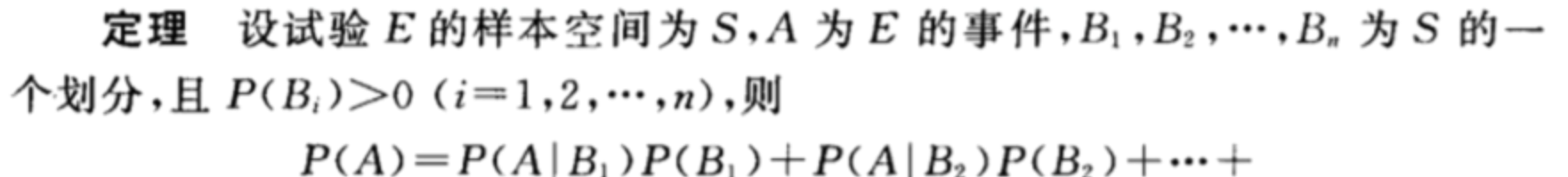
image.png

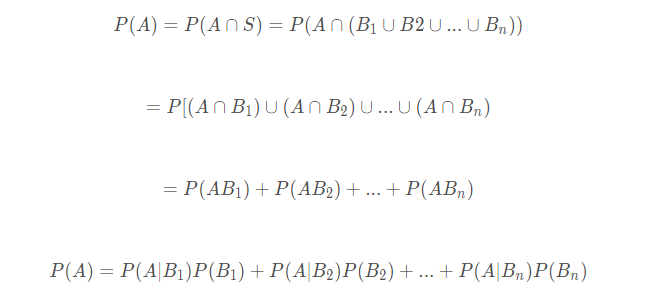
image.png

image.png

例题
image.png**

全概率公式

image.png
证明如下：
image.png

例题：
image.png

贝叶斯公式

image.png
证明如下：
3.1 概率基础 - 图15
即分子用条件概率展开，改为前验概率来计算后验概率。分母用全概率公式展开。

例题
image.png
image.png

image.png

独立性

判断方法：P(AB)=P(A)P(B)则称A与B独立

定理：
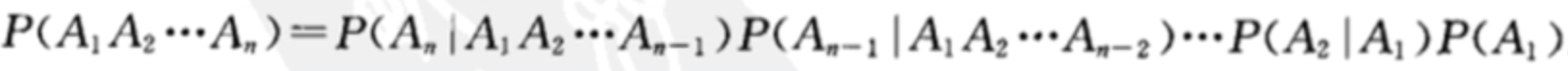
image.png
证明定理二：
image.png