1.7 矩阵对角化二次型

相似矩阵

注意 A的特征多项式就是；
证明定理3：
因为A与B相似，所以根据定义，B的特征多项式可以写为： 所以A、B的特征多项式是相同的，特征多项式相同那么解出来的特征值也是相同的。
但注意特征向量不一定相等。

定理3可以推出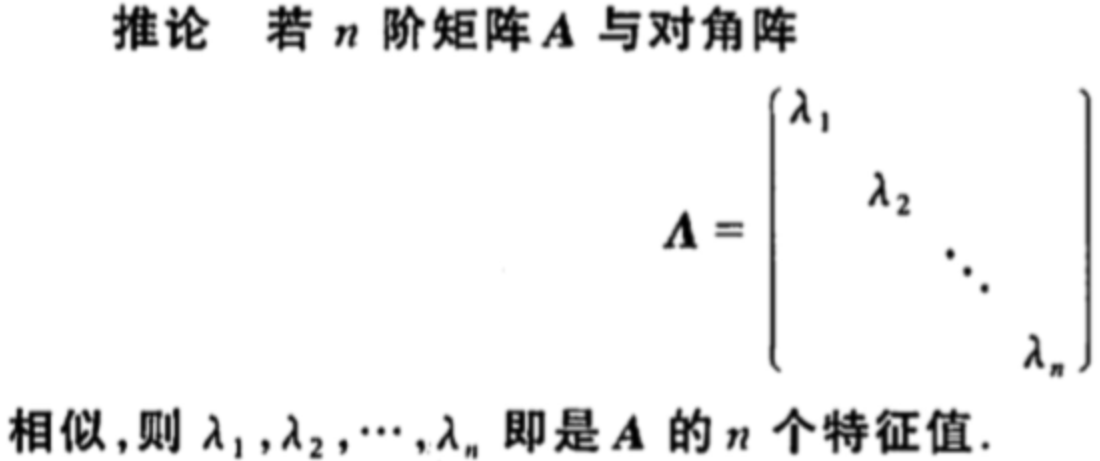

证明：

矩阵的对角化

基础概念

下面我们要讨论的主要问题是：对n阶矩阵A，寻求相似变换矩阵P，使为对角阵，这就称为把矩阵A对角化。也就是A与对角阵相似。
(只有对角线上有非0元素的矩阵称为对角矩阵)
假设已经找到可逆矩阵P，使为对角阵，我们来讨论P应满足什么关系：


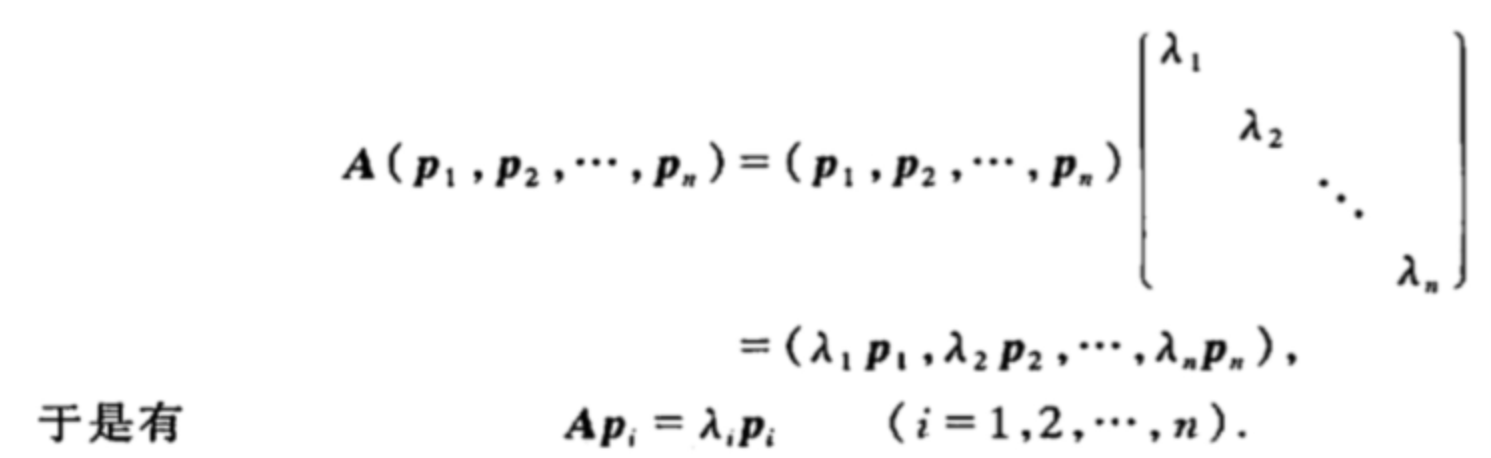
这个时候我们发现上式跟计算特征值的公式相近。也就是要使矩阵对角化，也是要求这样的特征向量。
从而推出定理4：

证明必要条件：
按照上图流程可以解出矩阵A的n个特征向量，有。因为P是可逆矩阵，所以列向量是线性无关的。
证明充分条件：
若A有n个线性无关的特征向量，则有，，…，，即，可以写作
也就是，接着可以转换为：
. 即A与对角阵相似。
注意要实现这一步转化需要满足P可逆，而P可逆的充要条件就是其列向量线性无关。
如果P不可逆，只能推到这一步，但是无法说明A能对角化，所以定理4强调A有n个线性无关的特征向量这一条件。

从而可以推出：

证明：A的n个特征值互不相等，根据定理2，特征向量是线性无关的，那么再根据定理4可以证得n阶矩阵A能对角化。

总结一下，n阶矩阵A与对角阵相似，则A有n个线性无关的特征向量；
A有n个特征值各不相等，则对应的特征向量线性无关，则A与对角阵相似。

但要判断一个矩阵能否对角化还是比较麻烦，因此下面来探究如何比较方便地判断？

对称矩阵的对角化

这里只探究比较特殊的对称矩阵()。

这里定理6要注意，定理2说的是方阵A的特征值各不相等则对应的特征向量线性无关，而这里A是对称阵，所以若特征值各不相等推出来的是 对应的特征向量正交。这里推出来的结果更强，因为与正交可以推出两者线性无关（上一章节的定理1：若n维向量是一组两两正交的非零向量，则线性无关），但反过来不成立。

证明：任何一个对称矩阵都可以对角化。且必有正交阵P使其正交化。
证明：首先，任何一个矩阵A都跟上三角矩阵相似。然后当A为对称矩阵时，假设这个上三角矩阵是B，则有：
，两边转置后得：，因为对称矩阵，则，因为P是正交矩阵，所以，所以式子可以化为：
，即，而已知B是上三角矩阵，所以B是对角矩阵。
所以对称矩阵A可以对角化得证。
然后因为P是正交阵，，即，所以

简单来说：

1. 之前我们知道在计算矩阵特征值时，如果特征值解出重根，对应的特征向量可能也是相同的。而这里强调的就是如果该矩阵A是对称矩阵，那么有多少特征值的重根，就能得到多少个线性无关的特征向量。并且重数相加之和为n
2. 上面定理6是 当特征值各不相等时，对应的特征向量两两正交。而当有重根时，例如有重根、，则对应的特征向量线性无关，