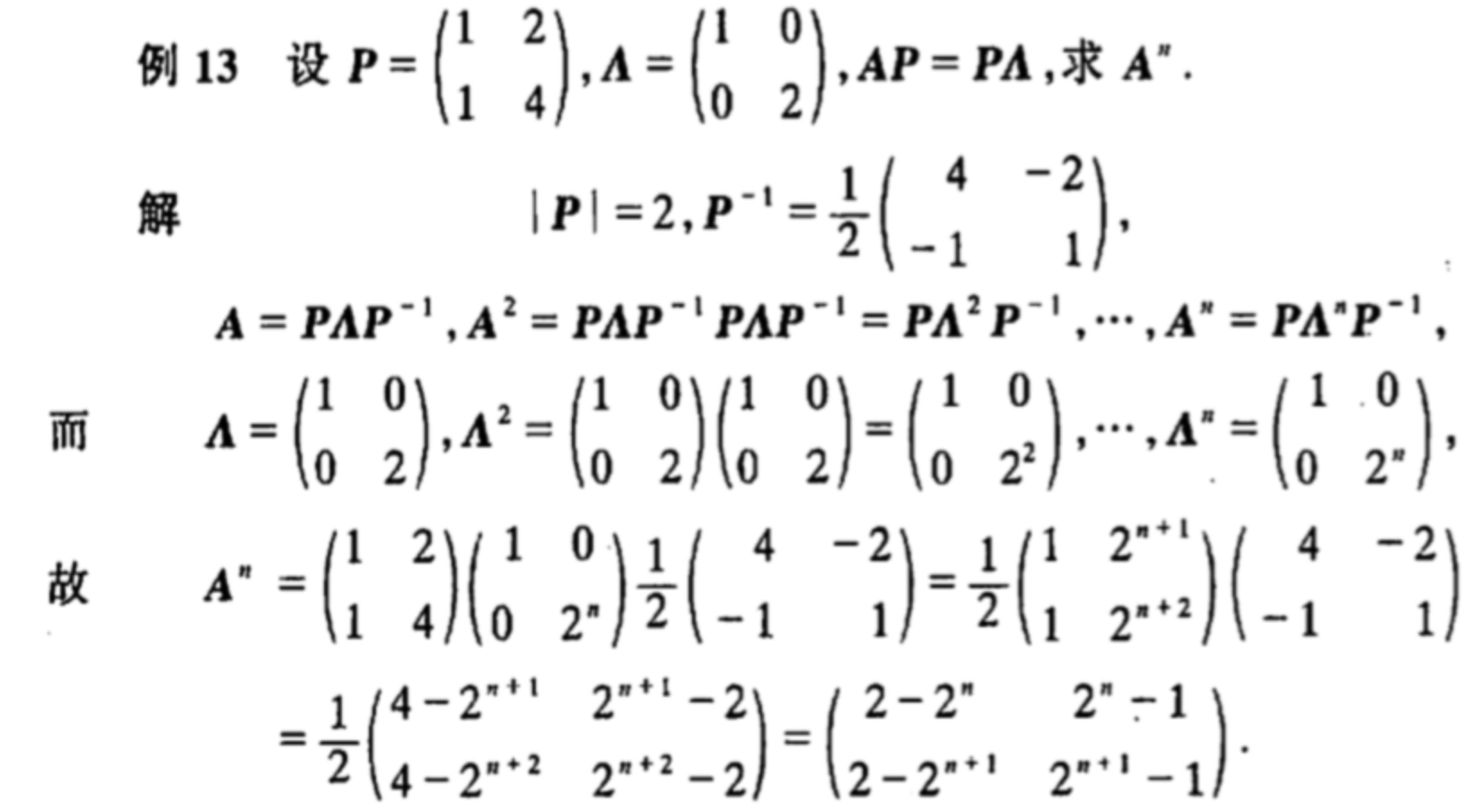先导知识
要计算矩阵的逆，先要有一些内容的铺垫;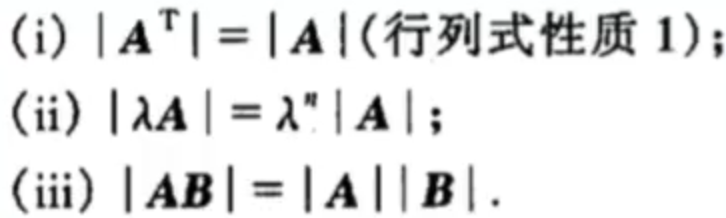
伴随矩阵
概念
注意两点：
1. 伴随矩阵中每一项代数余子式都是**实数**。1. 代数余子式的下标要注意，有**转置**！
性质
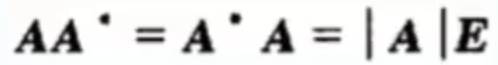<br />**证明：**<br />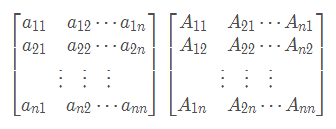<br />以上两个矩阵相乘结果也是矩阵，我们可以计算出结果中的应该为上面左边矩阵的第一行乘上右边矩阵的第一列：<br />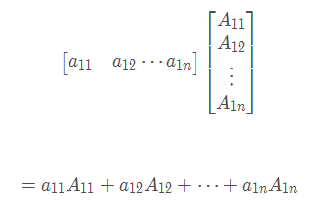根据行列式的展开的定理（上节中的**定理3**：行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和）可知，上面式子结果为：|A|.<br />以此类推，X对角线上都是|A|。<br />再看其它位置，例如计算：<br />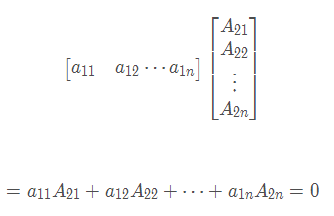根据上一节的推论<br />从而得到X的对角线位置以外的值都为0，即：<br />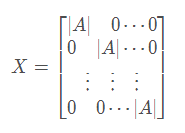，由于|A|是常数，所以可以把上面的|A|从矩阵中提取出来，则有：<br />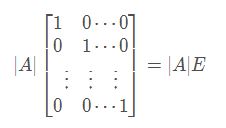，所以得证。
逆的定义
定理2证明如下：
由上述伴随矩阵的性质，
因为|A|不为0，两边同时除以|A|，得
，
所以根据逆的定义公式 AB=BA=E，A存在逆矩阵
，得证。
可以推导：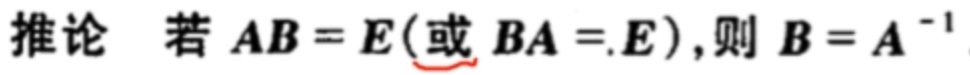
证明：AB=E → |A||B|=1 → |A|不为0 → A可逆，且A的逆阵唯一 → 
→ 
逆矩阵的性质
证明(iv): 因为A可逆，所以|A|不为0，由上面行列式性质1得 
，所以
也可逆；
而 
，所以得证。
引出二阶矩阵的逆的快速计算公式：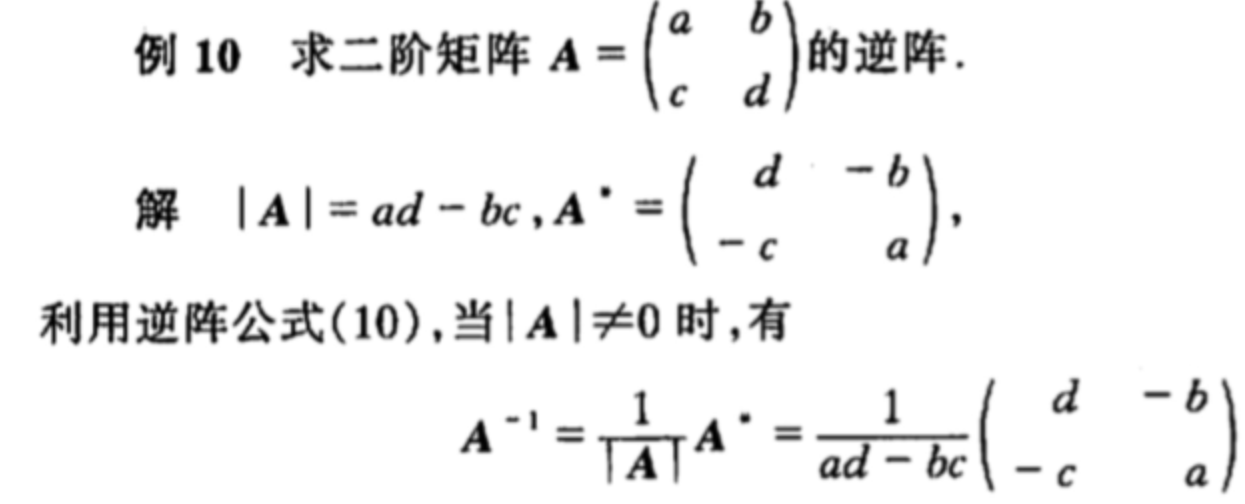
矩阵的n次幂
矩阵的对角化
若有收获，就点个赞吧
0 人点赞
