引入

无约束最优化问题是机器学习中最普遍、最简单的优化问题

求最大值也可以在前面加上负号，变成上面求最小的形式。

梯度下降法

要求一般有两种方法：

1. 令，但是很多复杂的函数求导后没法解出x，所以这种方法实际上很少用。
2. 基于迭代的方法，从某个点开始逐渐找很多点，使得这些点满足：，即找到x使逐渐变小。根据梯度的定义我们知道让x沿着梯度的负方向走可以使下降最快，所以，这里是用单位向量来表示方向，表示步长。有时候把常数看作一个整体直接写成：。通项就是：

所以该方法称作梯度下降法。
**
那么这个步长要如何取值呢？

1. 从机器学习的工程角度

一般初始选择之间，在迭代过程中逐渐衰减，比如。

1. 从数学角度来估计

令，这是一个关于的函数。因为我们要求的最小值，所以从 数学的角度就是要分析取多少使得最小，那就很自然地对求导，即：

然后求解出，但不一定都能解出来（要看f(x)具体的表达式）。

在机器学习中上式的目标函数其实就是损失函数。我们知道机器学习中会有很多样本，则总体的损失函数为，将所有样本损失函数相加后再求导，运算很慢。而且在工程中要将所有样本都装到内存里也是难以实现的。

随机梯度下降法

简单来说，就是每次只有一个样本来计算损失函数，求梯度，更新。
例如从，只用第一个样本来求然后求梯度更新。
每一次只用一个样本来进行梯度计算虽然速度很快，但是单个样本的梯度方向可能与整体样本的梯度方向相差甚远，这样整体的损失函数可能会被少数的异常样本带偏。

所以上述两种方法各有优劣，从而引出下面的

Batch梯度下降法

即每次迭代更新不像随机梯度下降那样只依赖单个样本，也不像梯度下降那样要累加所有样本的损失函数，而是累加一个批量的样本。
例如取batch size=100，
从的梯度就使用来计算；
从的梯度就使用来计算；
直到将全部样本算完一遍就是一个epoch。

牛顿法

第一种角度解释

我们要求，之前提过一种方法是求解，那么我们令。
然后要求解就是要找到函数与x轴的交点。那么我们可以用如下的迭代方法：

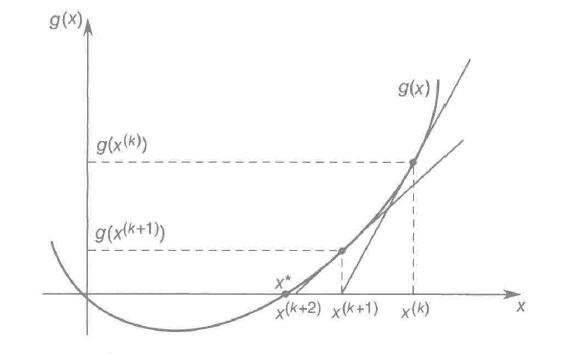
假设g(x)是如图所示的曲线，那么要求得与x轴的交点可以先做某个点的切线，假设该切线与x轴相交的点为，再做点的切线，假设该切线与x轴的交点为，….，就能不断迭代逼近g(x)=0的解。
从数学公式上来看，先求第一条切线方程：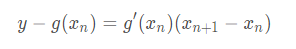

令y=0求得：

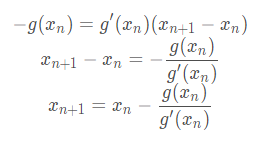
再把代回来就有：

这是二维的情况，如果是多维的情况，则，f(x)一阶导就是求梯度，二阶导就是Hessian矩阵。所以转变为：

在机器学习中计算Hessian矩阵的逆矩阵很麻烦，于是就引申出很多种拟牛顿法，例如BFGS（用另一个矩阵来逼近Hessian矩阵的逆矩阵）

第二种角度解释

假设f(x)是一个复杂的曲线，如下图：

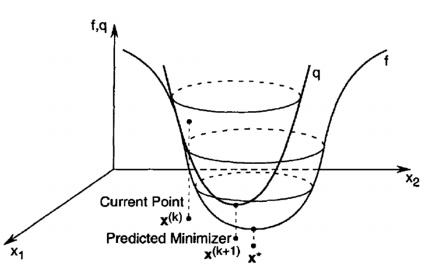
我们可以在一点上用一个二次函数g(x)进行拟合，找到拟合函数g(x)的最低点，然后在上继续用二次函数拟合，不断迭代，向f(x)的最小值逼近。因为我们知道函数最小值处一般是凹的，周围局部是类似二次函数的，所以我们用二次函数来拟合。
从数学公式来看，先写出g(x)在的泰勒展开（只用写到二阶导）：

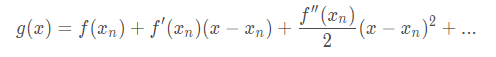
易得，所以上面的泰勒展开就是拟合的二次函数。
那么下面要求g(x)的最小值，由初中知识对称轴为：，观察g(x)可得：


因此最低点为：

注意：牛顿法一开始选中的点如果离最小值太远有时候无法收敛，选择接近最小值的点再拟合收敛效果更好。因此经常是使用梯度下降到局部最小值附近后再用牛顿法继续逼近。

牛顿法收敛速度

要计算收敛速度，就是比较一下到的距离和到的距离的区别，所以下面开始转化：

根据拉格朗日中值定理，上式可以化为：

这里再用一次拉格朗日中值定理得到：

令，则上式变为：

因为，所以

由于M的分子分母都是导数，导数都是有界的，所以M是有界的，用表示其上界，则

即

通过上式我们可以得到两条结论：

1. 牛顿法是二次收敛的，例如到的距离为0.1，则到的距离小于0.01乘以一个常数。
2. 牛顿法要在局部最小值附近使用，例如如果到的距离大于1，即上式中，那么距离的上界会越来越大无法收敛。