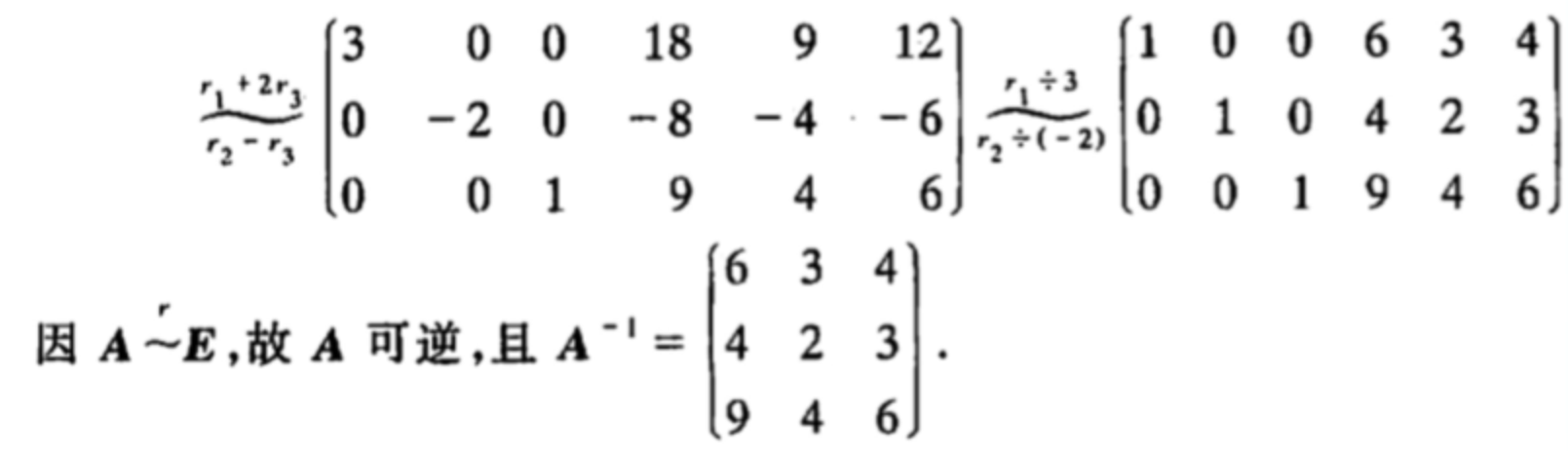1.矩阵的初等变换
引入

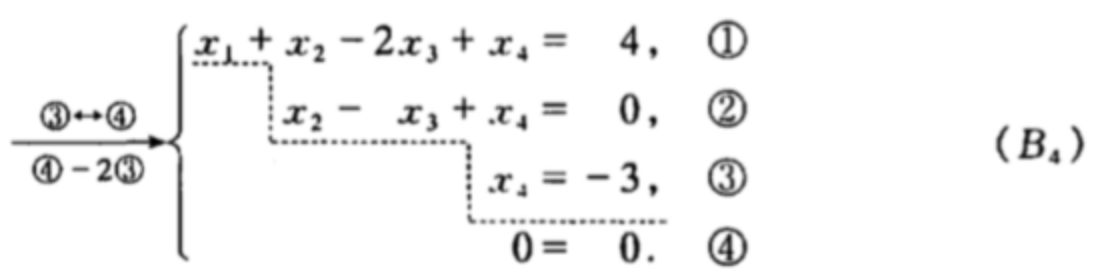
以上例子实际上是把线性方程组的系数,连带常数项(等号右边的数字)看做是一个矩阵(行话叫:增广矩阵),然后对这个增广矩阵做了一系列的变化,最后可以判断方程组的解的形态。
在解线性方程组时,由上面观察得到矩阵的基本变换,我们在下面进行统一定义:
定义

举个例子:


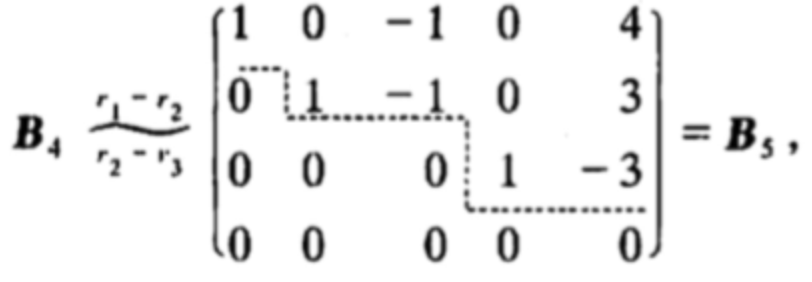

进而做出一些约定:
2.逆矩阵的另外一种求法
引入

上述的三种初始变换其实对应了三种初等矩阵,矩阵的本质就在于此:矩阵就是用来做变换的。
其中交换两行,对应的矩阵就是下面的矩阵:
以不为0的数k乘以某一行(列)中的所有元素,对应的初等矩阵为:
把某一行所有元素的k倍加到另一行对应的元素上去,对应的初等矩阵为:
性质

性质1即:初等行变换,左边乘对应初等矩阵,初等列变换,右边乘对应初等矩阵
性质2证明:
先证必要条件, 所以
(三种初等矩阵的行列式分别为-1,k,1 )。所以A可逆。
再证充分条件,由第一节最后的定理可得,A总能通过初等变换转换成标准型,这里记为B,所以有,因为A可逆所以|A|不为0,所以等式右边的行列式也不为0,即标准型B的行列式不为0。

由标准型的定义可知B为单位矩阵E,所以
<br />证明:<br />由上面性质2可得,当A可逆,,即A可以通过l次初等行变换转换为E。同理反过来也符合。<br />并且除了行等价,列等价也符合该推论。
逆矩阵的另一种求法
之前讲的求逆矩阵需要通过伴随矩阵来计算,但当矩阵的阶数较大时,计算代数余子式的计算量较大。
所以可以使用以下方法:
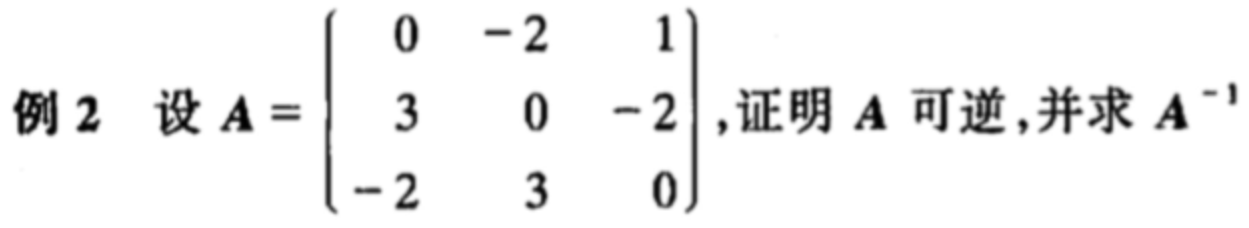
证明
证明该方法为何可以算出A的逆矩阵:
要求A的逆矩阵,先把A和E摆在一起得到 (A E),然后对这个增广矩阵做初等行变换,也就是要在左边乘上,把
的乘积结果记为P,则对(A E)做初等行变换可以看作计算 P(A E)。而结果我们要使增广矩阵左边的矩阵A变为单位阵E,即(A E)变为(E Q),用数学公式表示就是:P(A E) = (E Q) 。该式可以看作PA=E,PE=Q。所以得到:
, 也就是