泰勒公式

佩亚诺余项

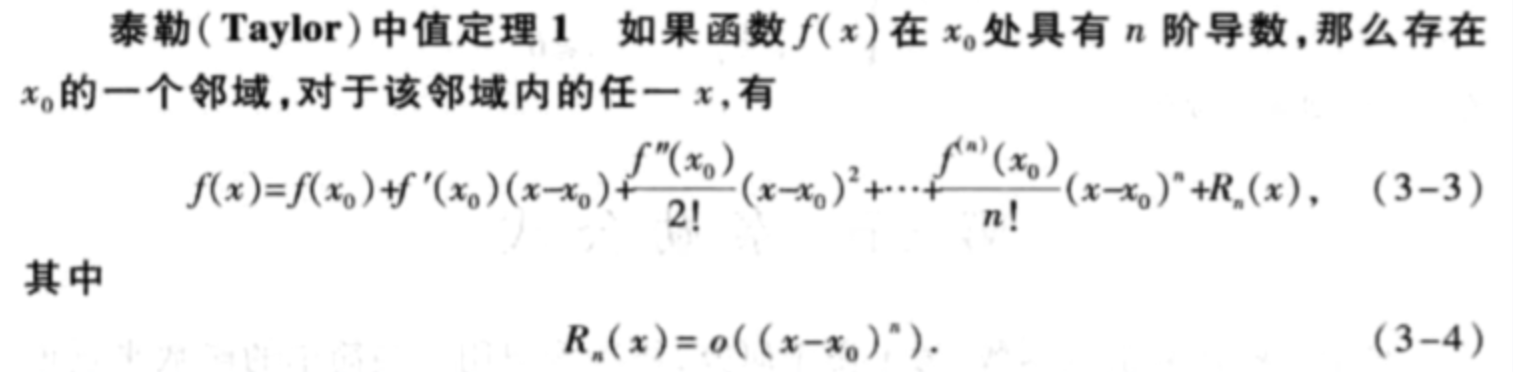
总结：任意一个函数都可以在展开，写成一个多项式的形式。但这样肯定是近似相等的，所以R(x)就是它的误差，也称作的高阶无穷小。也就是当趋近0时，R(x)比它小得更快。
高阶无穷小也可以这样理解：

拉格朗日余项

可以证明这里的R(x)与佩亚诺余项其实一样还是高阶无穷小。

麦克劳林展开

上面泰勒公式中，当时，称作麦克劳林展开。

举例：

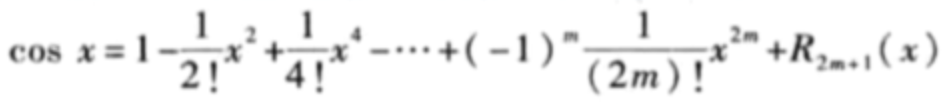
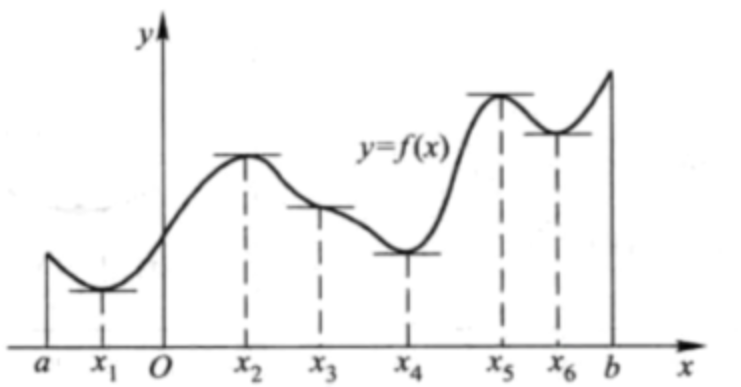
函数的凹凸性

判断方法总结：用函数的二阶导数来判断凹凸性。

为什么可以用二阶导数判断：
然后右式再用一次拉格朗日中值定理为，所以整个式子是否大于0取决于

函数的极值

定义

定理

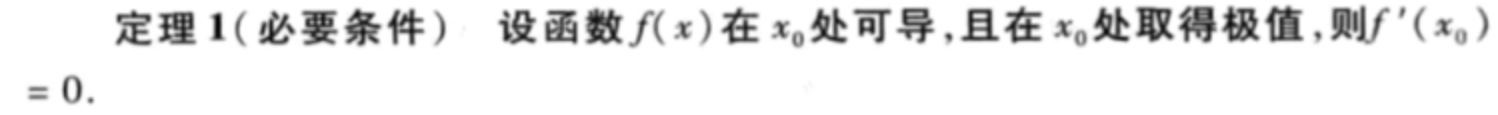
理解： 极值点 可以推出 导数为0

理解： 两边的导数异号，可以推出极值点

理解：一阶导数为0且具有二阶导数，可以推出极值点
这里可以通过函数的凹凸性来理解，也可以通过泰勒公式在展开来理解。
，最后的误差当时可以 忽略不计，而，则上式转化为：，
当，，所以在附近都大于，即为极小值。
当，，所以在附近都小于，即为极大值。
注意这里的前提是在附近，否则一开始泰勒公式展开时的误差就无法忽略。