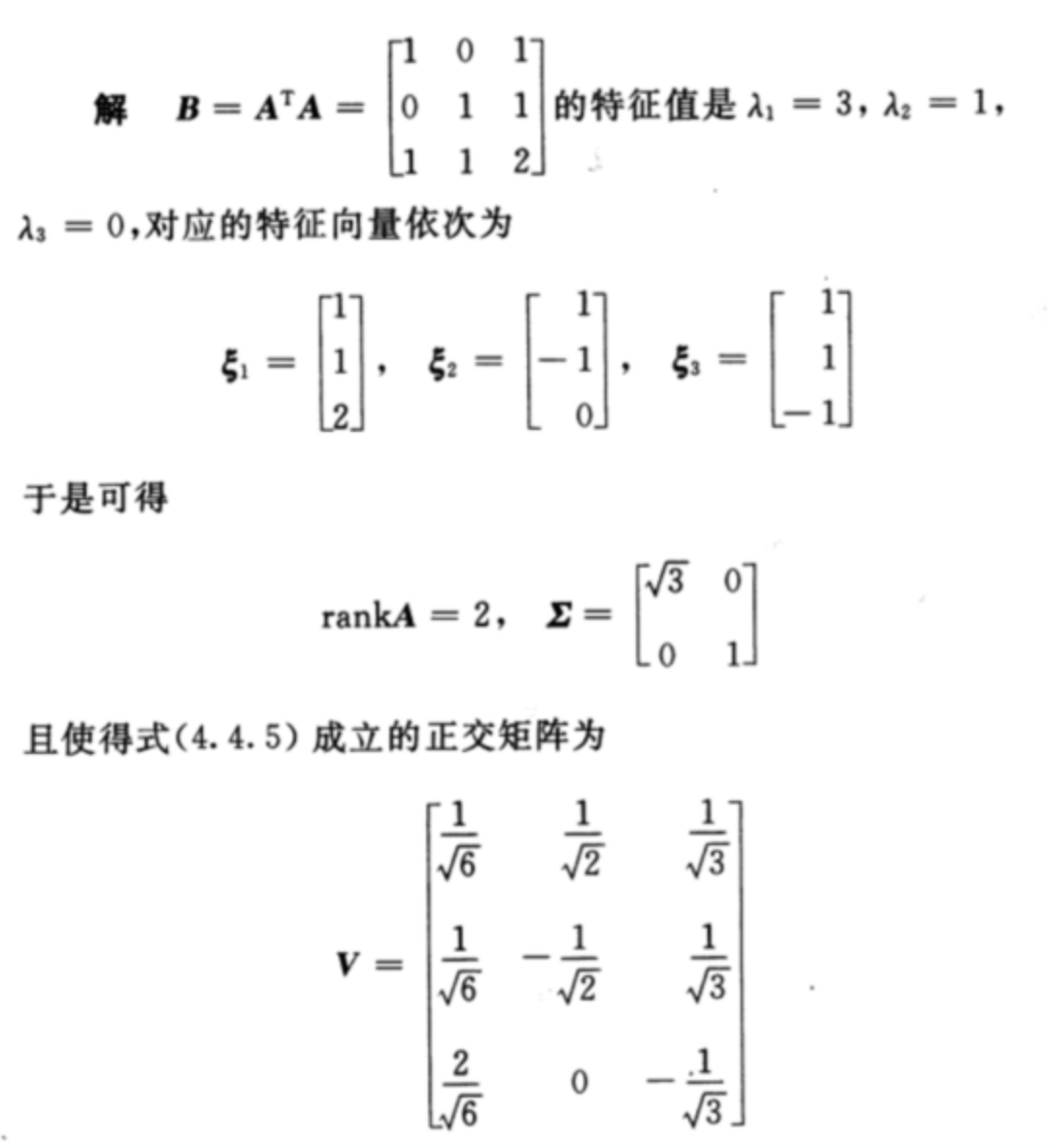
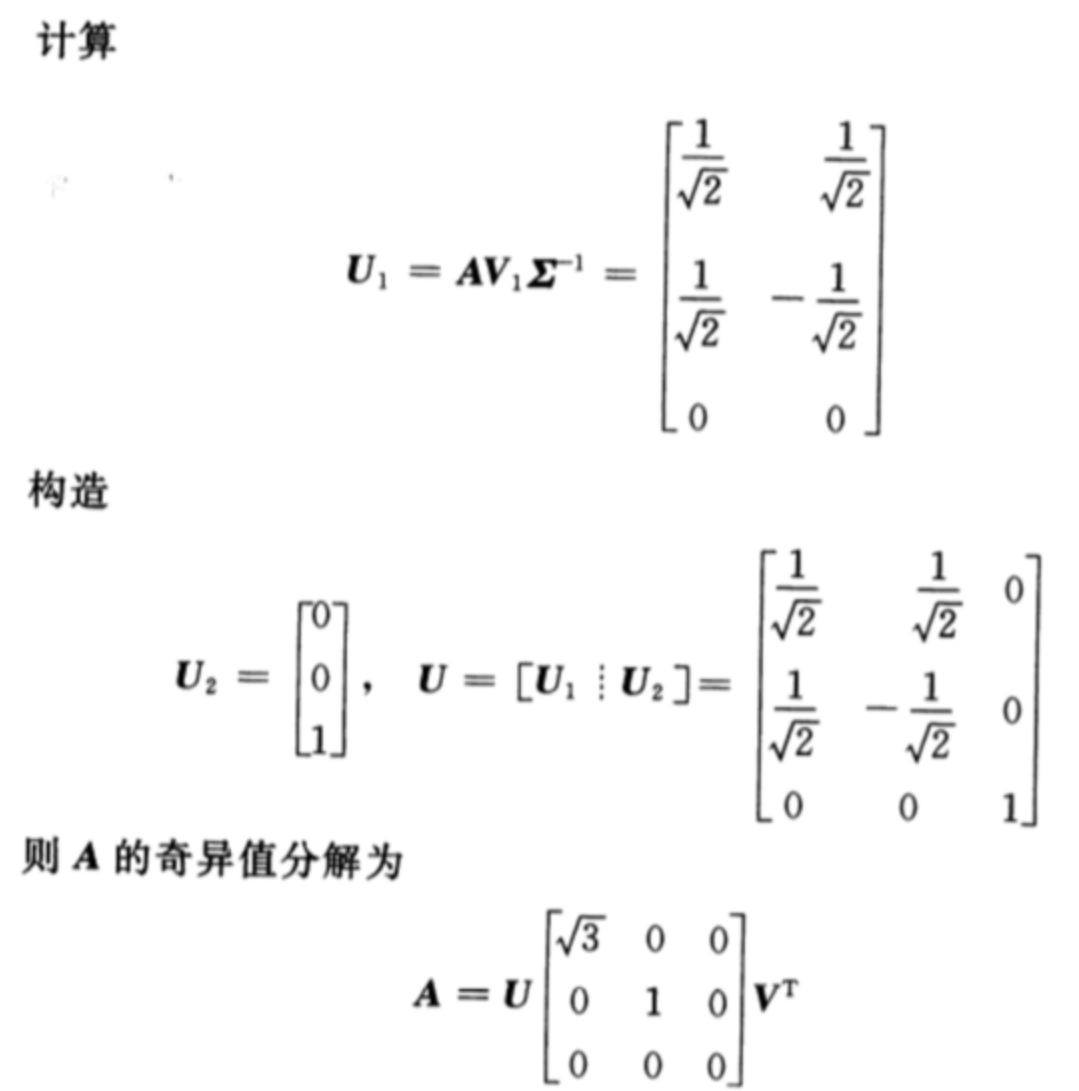
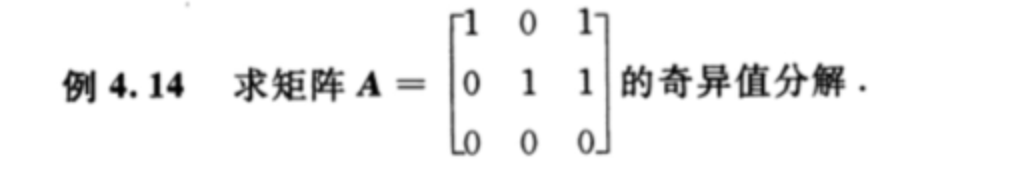引入

矩阵对角化总结

1. 如果矩阵有n个线性无关的特征向量，则存在矩阵P使得。这里P就是由这n个线性无关的特征向量所构成的，而对角阵对角线上的值就是A的n个特征值。
2. 如果矩阵即A是对称阵，则一定存在正交矩阵P使得

假设我们要处理一个1080*720分辨率的一张图片，想把它分解成一个对角矩阵两边乘以简单矩阵的形式。但是很明显这张图片表示的矩阵不是方阵，找不到这样的对角矩阵。
所以面对这样的一般矩阵要如何处理，就是下面要介绍的奇异值分解。

奇异值分解

预备知识

这里对实数矩阵矩阵其实就是，对复矩阵就是取一次共轭再做转置。
（1）证明：而这里我们只讨论实矩阵，所以（1）就是要证明的特征值都是非负实数。而上一节我们讲了是一个半正定阵（要判断是否是正定矩阵，就要用一个试探向量x，得），所以的所有特征值都是大于等于0的.
（2）证明：这里其实就是要证明与的解空间是一样的，因为N(A)+R(A)=n。那么可以尝试证明与的解是否是一样的。首先易得对所有，都有。然后对所有，都有，即，而Ax是一个列向量，所以。这样我们就证明了与的解是完全一样的，那么与的解空间N(A)是一样的。又因为r(A)=n-N(A)，所以他们的秩也是一样的。
（3）证明：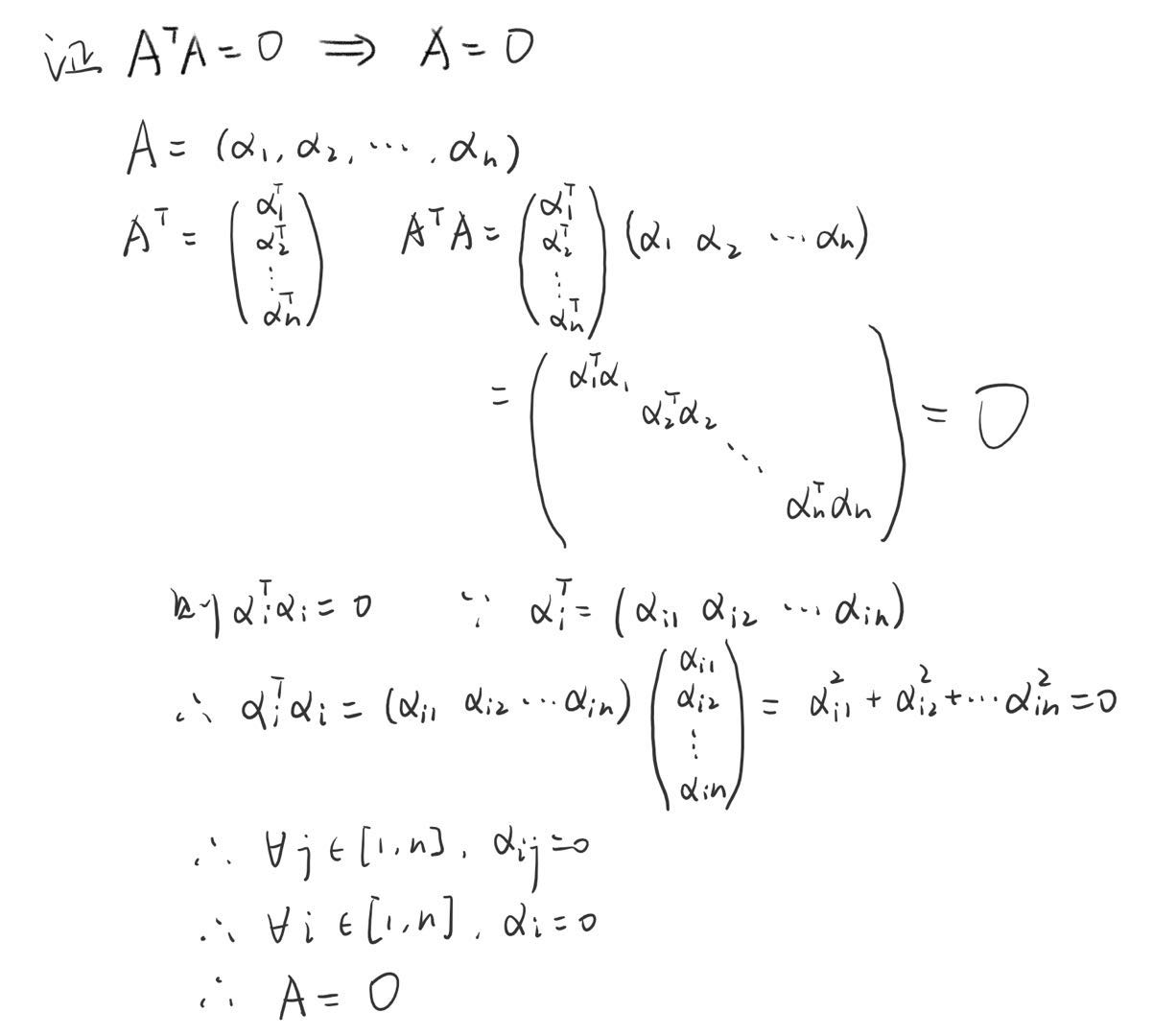

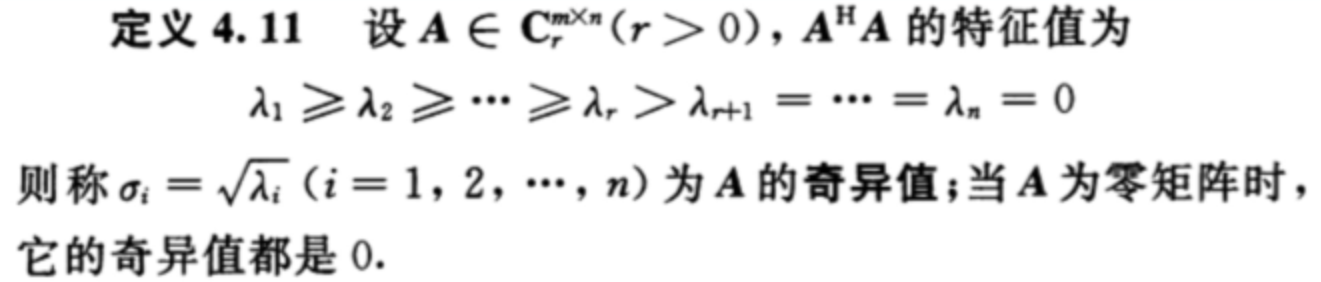
证明：首先，所以根据上述的性质（2）有。因为是对称矩阵，所以，且的对角线上分别是A的特征值。又因为对可逆矩阵P，Q，如果，则R(A)=R(B)，所以，所以，所以有r个特征值是大于0的。

SVD分解

注意这里酉矩阵是对包含复矩阵而言，对实矩阵就是正交矩阵，即.
另外注意这里的不一定是方阵。

以上就是任意一个矩阵的奇异值分解的证明，并且也是矩阵奇异值分解的过程，即找到一个简单的矩阵和两个正交矩阵，将其表示成简单的形式。

下面举个例子辅助理解：