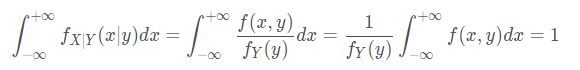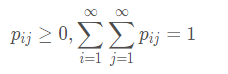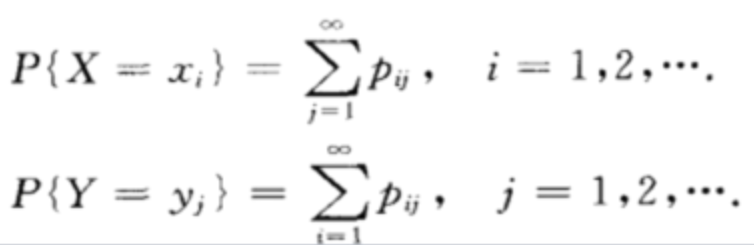掌握目标

  1. 掌握常用离散随机变量分布
  2. 掌握常用连续随机变量分布，分布函数与概率密度函数的意义
  3. 了解随机变量函数的分布的求法
  4. 掌握多元随机变量(离散和连续),以及边缘分布和条件分布

    离散随机变量

    0-1分布

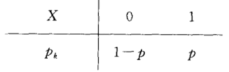
    image.png
    例如丢硬币，只丢一次。

    伯努利分布，二项分布

    3.2 随机变量与多维随机变量 - 图3
    是0-1分布的推广，也可以是丢硬币，但是这里是丢n次，有k次正面朝上的概率。

泊松分布

image.png

image.png

连续随机变量

定义

因为连续随机变量取离散值计算概率时没有意义，所以这里引入分布函数：
3.2 随机变量与多维随机变量 - 图6
那么
3.2 随机变量与多维随机变量 - 图7
总结：x在x1和x2之间的概率等于x2的概率减去x1的概率

性质

image.png

例题
image.png

image.png

概率密度函数

定义

image.png
也就是3.2 随机变量与多维随机变量 - 图12，根据极限的定义可以表示如下：
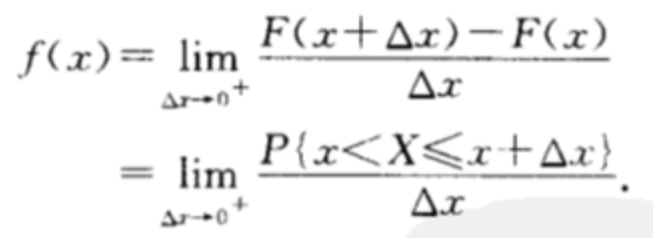
image.png
从几何角度来看就是：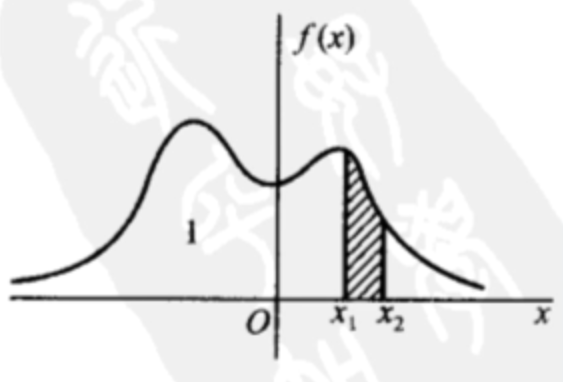
image.png
上图中3.2 随机变量与多维随机变量 - 图15相当于3.2 随机变量与多维随机变量 - 图16，概率密度相当于概率除以单位长度3.2 随机变量与多维随机变量 - 图17，所以f(x)就是单位概率。
因为连续随机变量中没办法取离散值，所以就引入这种单位长度上概率的概念。

性质

  1.      1. ![](https://cdn.nlark.com/yuque/__latex/89e4900ab16ff046b5b0448ecd94e38e.svg#card=math&code=f%28x%29%5Cge%200&height=20&width=62)
  2.      1. ![](https://cdn.nlark.com/yuque/__latex/ffab48b1a932d1770c0f58f44a447066.svg#card=math&code=F%28%2B%5Cinfty%29%3D%5Cint%20_%7B-%5Cinfty%7D%5E%7B%2B%5Cinfty%7Df%28t%29dt%3D1&height=45&width=195)

常见的概率密度函数

（一）均匀分布

image.png

（二）指数分布

image.png

（三）正态分布

image.png

image.png（服从标准正态分布）

随机变量函数的分布

离散随机变量

image.png

连续随机变量

image.png

总结一下求解随机变量概率分布的通用思路（先求分布函数再求导）：
image.png
**
补充说明转换为3.2 随机变量与多维随机变量 - 图25后如何求导：
image.png

多维随机变量

离散型

定义
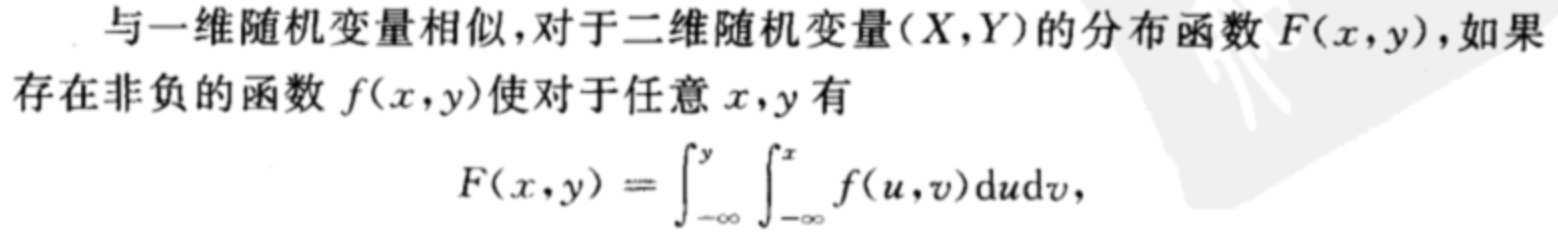
image.png

例题**
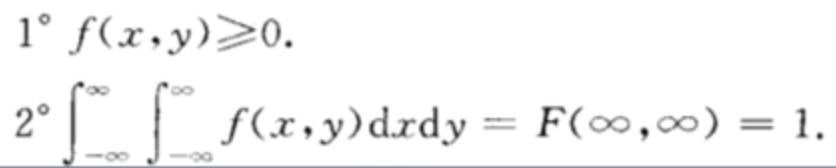
image.png

联合分布函数3.2 随机变量与多维随机变量 - 图29，该函数满足image.png

连续型

定义
image.png
性质
**image.png

image.png

总结：之前一维随机变量概率密度相当于概率除以单位长度，而这里二维随机变量概率密度则是概率除以单位面积，即随机变量X，Y落在单位面积上的概率。

边缘分布和条件分布

例如对于二维随机变量，我们只关心X一个变量，那么就固定X=x，把Y所有取值的概率相加起来，叫做边缘分布

离散型边缘分布

image.png

连续型边缘分布

3.2 随机变量与多维随机变量 - 图35
3.2 随机变量与多维随机变量 - 图36

离散型条件分布

上面求边缘分布，其实就是为了求条件分布，即：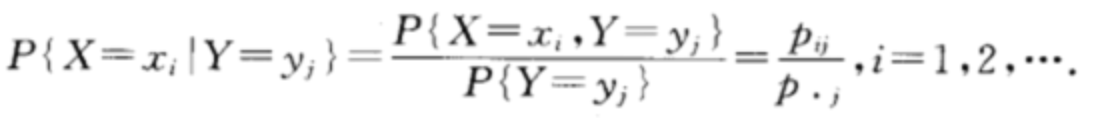
image.png
这里分母就是上面求的边缘分布。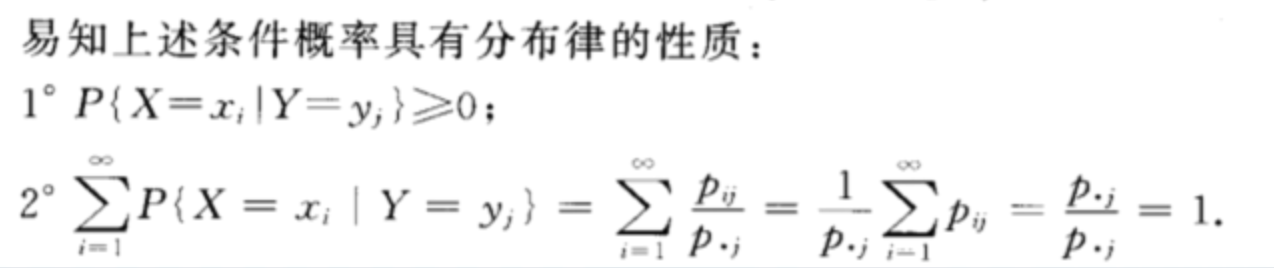
image.png

连续型条件分布

如果是连续型，则有条件概率密度：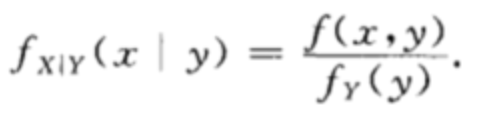
image.png
也满足概率分布的两个特性，即概率大于等于0，求和等于1。
image.png

独立性

离散型

3.2 随机变量与多维随机变量 - 图41

连续型

3.2 随机变量与多维随机变量 - 图42