1.5 矩阵的秩

概念

定义

定义4就是矩阵的秩的定义。

性质

举个例子方便理解秩的定义：

求解矩阵的秩

定理

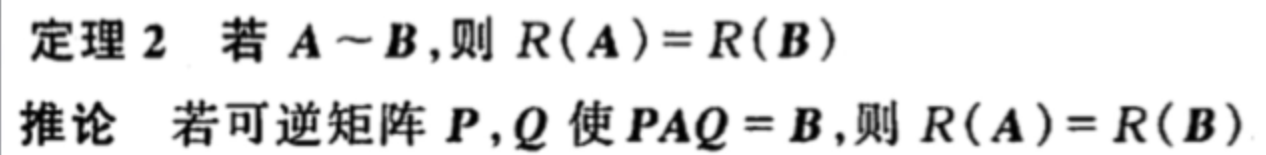
定理2证明： 对A进行初等变换时，并不会影响其中子式的行列式，所以R（A）= R（B）
推论证明：由上一章节的性质2可得，可逆矩阵P可以看作，所以
，即对A与B等价，则由定理2可得R（A）= R（B）

根据上述定理，我们知道对矩阵A进行初等变换不会改变矩阵A的秩，因此当矩阵的行数与列数较高时我们可以用初等变换把矩阵化为行阶梯形矩阵来求解矩阵的秩。
下面举个例子：

秩的性质

上述性质在前面均已提到过，下面再介绍几个常用的秩的性质：

性质7证明：由性质4，当P可逆，Q为单位阵E时，R（PA）= R（A）。即当A可逆，R（AB）= R（B）。
当A、B不可逆时，，
当A或B为单位阵时，
性质7很重要，在后面推导多元线性回归的时候要用。

线性方程组的解

n为元数，m为约束。
之前有讲到对方阵的克莱姆法则，而这里的是更一般的情况，即m和n不等。

对定理3的直观理解：
(i) 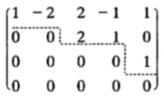通常是比较窄的增广矩阵，即m>n，约束较多。此时R(A)(ii) 此时方程和变量一一对应，所以有唯一解；
(iii) 一般是m
定理4证明：
这里相当于右边常数项b为0，即R(A)=R(A,b)，所以满足定理3的(ii)、(iii)，该方程组一定有解。
但当R(A)=n时，方程组有唯一解x=0，而我们要非零解。所以R(A)<n.

当A为n*n方阵时，可以从1.2章节中的克莱姆法则的角度来看：AX=0有非零解的充要条件是|A|=0。
而矩阵A可逆，，R(A)=n，这三个是等价的。所以定理4中 R(A)所以该定理是克莱姆法则更广泛的推广。