SVD的应用

首先先回顾上一章节讲的SVD分解，就是在mn的矩阵A的左右两边分别乘以和，得到一个对称矩阵。最后通过证明矩阵A可以分解为这种形式：

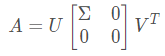
分析一下该式中各项的shape如下：
A：mn U：mm 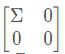：mn ：nn
如果矩阵A的秩R(A)=r，则是rr对角阵，其中对角线上的元素就是的不为0的特征值的平方根。把U写成列向量的形式为：，其中每个都是m维列向量，同理，V也可以写为，转置后变为，因此上式矩阵A可以展开为：

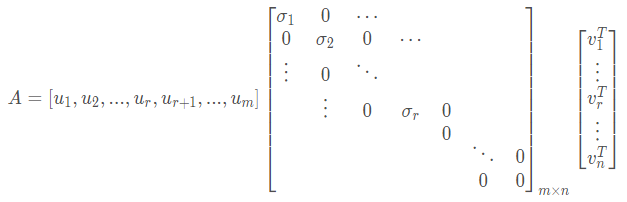
展开过程中我们观察到，因为中间矩阵的后n-r项都为0，所以矩阵的m-r项和的n-r项在矩阵计算过程中都相乘为0，所以上式就变为：

分析一下该式中个各项的shape：
：m1 ：1n 所以的shape为m*n，就和A的维度刚好对上。
注意这里之间是有大小关系的：，接下来我们看看这个性质在后面有什么应用。

图像压缩

实现方法

在图像处理中，图像信息是作为一个矩阵输入的。假设输入矩阵A是的，而每个点是float类型（即用4字节存储），那么在存储这张图像时就需要占用个字节的空间大小。
再看上式我们推导出的右边，其中虽然也是的，但是是m1的只有m个数，是1n的只有n个数，所以存储只要个字节的空间大小。
而上面我们已经知道，所以。并且一般前几项中的值都较大，而后面的都接近于0。这意味着前面的项已经包含了大部分的图片信息，后面的项相对不重要。
因此A可以用前k项的来近似表示，此时图片存储需要的空间为：，其中1是常数占用的空间，可以看到当时，，从而达到了图像压缩的目的。

损失

因为的模长为1，所以采用上述方法压缩图像造成的损失为：，也就是k越大，损失越小。举个例子：

可以看到

传统网络图片传输与现代传输的原理

传统

传统电脑加载图片时，都是从第一行的像素点开始传输，然后我们会看到图片是一行一行的加载出现，效果如下：

现代

而现在我们打开图片时会发现照片是从不清晰到清晰，可能就是利用SVD分解，一开始先传输前5个，然后逐渐增加k，即传送更多的，所以就会产生从不清晰到清晰的过程。

矩阵乘法加速

假设矩阵A的shape是200100的，A用SVD分解变成：，取前25项近似表示A：，把记为M，则
假设矩阵A跟一个1001的列向量x做乘法，Ax的乘法计算次数为次；
如果计算MNx，首先Nx的乘法计算次数为次，计算后shape为251，而M和Nx的乘法计算次数为次，所以MNx的乘法计算次数为*7500次。
并且由上面推导我们可以知道，计算MNx过程中空间存储也较低。

多元线性回归

最小二乘推导

现在有N个样本，每个样本对应，所以有：


…
注意这里代表向量(n1)的第1个分量，一共有n个分量
上式可以化作：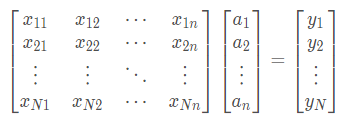

即我们要找到一组参数使得上式成立。上式还可以写作：

也就是要解这个线性方程得到系数。
当x的空间维度和样本个数一样的时候，也就是N=n（X是方阵），*且X可逆时，上式两边同时乘以X的逆矩阵：

但是这个是理想情况，而一般情况下，此时不可能成立，这个时候退而求其次，想办法使其左右两边尽可能的接近，一种办法就是让二者模长相减最小，即，要求最小值就是令这个二范数求导为0求解a，注意这里a才是变量，其它是参数。

也就是求解，而这里不一定可逆，因为它是半正定的，下面用试探矩阵U证明一下：

如果大于0就是正定矩阵。所以不一定可逆，因此下面分两种情况讨论：

当N>n，即样本数>参数个数

如N=5，n=3，一般是可逆的，因为，而X的秩很可能是3（因为可以把X看作5个三维空间上的点，只要找到3个点不在同一直线上，X的秩就为3。也就是从5行向量中找到3个线性无关的向量）。
所以当可逆时

其中也叫做X的伪逆，伪逆矩阵不一定存在。

当N<n，即样本数<参数个数

如N=3，n=5，此时是不可逆的，因为。
则此时要给最小二乘的J加一个正则项，即最小二乘+最小范数。也叫做岭回归。
此时

对J求导就变为
即转换为求解
其中必定可逆
（因为可以用一个不为0的试探向量a证明它是正定矩阵：

因为，，所以为正定矩阵，其特征值，而，所以其为可逆矩阵。）

所以可以解出a：
此时a就是最小二乘的基础上，还增加了对系数矩阵的最小范数的约束，希望a的范数尽可能小。也叫做岭回归。
**

总结

上述推导可见分为2种情况讨论很麻烦，所以一般不管N是否大于n，直接用岭回归来求解。所以最后的解一般是
一般不用伪逆。