CTC（Connectionist Temporal Classification）介绍

CTC 解决什么问题

CTC，Connectionist Temporal Classification，用来解决输入序列和输出序列难以一一对应的问题。

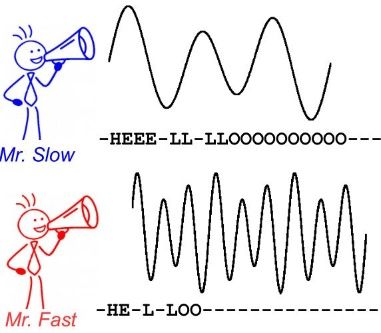
举例来说，在语音识别中，我们希望音频中的音素和翻译后的字符可以一一对应，这是训练时一个很天然的想法。但是要对齐是一件很困难的事，如下图所示（图源见参考资料[1]），有人说话块，有人说话慢，每个人说话快慢不同，不可能手动地对音素和字符对齐，这样太耗时。

再比如，在 OCR 中使用 RNN 时，RNN 的每一个输出要对应到字符图像中的每一个位置，要手工做这样的标记工作量太大，而且图像中的字符数量不同，字体样式不同，大小不同，导致输出不一定能和每个字符一一对应。

CTC 基本概述

考虑一个 LSTM，用 w 表示 LSTM 的参数，则 LSTM 可以表示为一个函数：y\=Nw(x)。

定义输入 x 的时间步为 T，每个时间步上的特征维度记作 m，表示 m 维特征。

x\=(x1,x2,…,xT)xt\=(x1t,x2t,…,xmt)

输出时间步也为 T，和输入可以一一对应，每个时间步的输出维度作为 n，表示 n 维输出，实际上是 n 个概率。

y\=(y1,y2,…,yT)yt\=(y1t,y2t,…,ynt)

假设要对 26 个英文字符进行识别，考虑到有些位置没有字符，定义一个 - 作为空白符加入到字符集合 L′\={a,b,c,…,x,y,z}∪{−}\=L∪{−}\={a,b,c,…,x,y,z,−}，那么对于 LSTM 而言每个时间步的输出维度 n 就是 27，表示 27 个字符在这个时间步上输出的概率。

如果根据这些概率进行选取，每个时间步选取一个元素，就可以得到输出序列，其输出空间可以记为 L′T。

定义一个 B 变换，对 LSTM 的输出序列（比如下例中的 4 个π）进行变换，变换成真实输出（比如下例中的 state），把连续的相同字符删减为 1 个并删去空白符。举例说明，当 T=12 时：

B(π1)\=B(−−stta−t−−−e)\=stateB(π2)\=B(sst−aaa−tee−)\=stateB(π3)\=B(−−sttaa−tee−)\=stateB(π4)\=B(sst−aa−t−−−e)\=state

其中π表示 LSTM 的一种输出序列。当我们优化 LSTM 时，只需要最大化以下概率，即给定输入 x 的情况下，输出为 l 的概率，l 表示真实输出。对下式取负号，就可以使用梯度下降对其求最小。

假设时间步之间的输出独立，那么对于任意一个输出序列π的概率计算式子如下，

其中下标πt 表示的是，输出序列在 t 时间步选取的元素对应的索引，比如该序列在第一个时间步选取的元素是 a，那么得到的值就是 1。选取的是 z，那么得到的值就是 26。选取的是空白符，那么得到的值就是 27。为了方便观测，也用对应的字符表示，其实是一个意思，如下式所示。

π\=(−−stta−t−−−e)p(π|x)\=y1−⋅y2−⋅ys3⋅yt4⋅yt5⋅ya6⋅y7−⋅y8t⋅y9−⋅y10−⋅y11−⋅ye12

但是对于某一个真实输出，比如上述的 state，有多个 LSTM 的输出序列可以通过 B 转换得到。这些序列都是我们要的结果，我们要使给定 x，这些输出序列的概率加起来最大。如果逐条遍历来求得，时间复杂度是指数级的，因为有 T 个位置，每个位置有 n 种选择（字符集合的大小），那么就有 nT 种可能。因此 CTC 借用了 HMM 中的 “前向 - 后向算法”（forward-backward algorithm）来计算。

CTC 中的前向后向算法

由于真实输出 l 是一个序列，序列可以通过一个路径图中的一条路径来表示，我们也称输出序列 l 为路径 l。定义路径 l′为 “在路径 l 每两个元素之间以及头尾插入空白符”，如：

对某个时间步的某个字符求导（这里用 k 表示字符集合中的某个字符或字符索引），恰好是与概率 ykt 相关的路径。

∂p(l|x)∂ykt\=∂∑B(π)\=l,πt\=kp(π|x)∂ykt

以前面的π1,π2,π3,π4 为例子，画出两条路径（还有两条没画出来），如下图所示（图源见参考资料[1]）。

4 条路径都在 t=6 时经过了字符 a，观察 4 条路径，可以得到如下式子。

π1\=b\=b1:5+a6+b7:12π2\=r\=r1:5+a6+r7:12π3\=b1:5+a6+r7:12π4\=r1:5+a6+b7:12

p(π1,π2,π3,π4|x)\=y1−⋅y2−⋅y3s⋅y4t⋅y5t⋅y6a⋅y7−⋅y8t⋅y9−⋅y10−⋅y11−⋅y12e+y1s⋅y2s⋅y3t⋅y4−⋅y5a⋅y6a⋅y7a⋅y8−⋅y9t⋅y10e⋅y11e⋅y12−+y1−⋅y2−⋅y3s⋅y4t⋅y5t⋅y6a⋅y7a⋅y8−⋅y9t⋅y10e⋅y11e⋅y12−+y1s⋅y2s⋅y3t⋅y4−⋅y5a⋅y6a⋅y7−⋅y8t⋅y9−⋅y10−⋅y11−⋅y12e

令：

forward\=p(b1:5+r1:5|x)\=y1−⋅y2−⋅y3s⋅y4t⋅y5t+y1s⋅y2s⋅y3t⋅y4−⋅y5abackward\=p(b7:12+r7:12|x)\=y7−⋅y8t⋅y9−⋅y10−⋅y11−⋅y12e+y7a⋅y8−⋅y9t⋅y10e⋅y11e⋅y12−

那么可以做如下表示：

p(π1,π2,π3,π4|x)\=forward⋅yat⋅backward

上述的 forward 和 backward 只包含了 4 条路径，如果推广一下 forward 和 backward 的含义，考虑所有路径，可做如下表示：

∑B(π)\=l,π6\=ap(π|x)\=forward⋅yat⋅backward

定义 forward为αt(lk′)，表示 t 时刻经过 lk′字符的路径概率中 1-t 的概率之和，式子定义如下。

αt(lk′)\=∑B(π)\=l,πt\=lk′∏t′\=1tyπt′t′

t=1 时，符号只能是空白符或 l1，可以得到以下初始条件：

α1(−)\=y1−α1(l1)\=yl11α1(lt)\=0,∀t>1

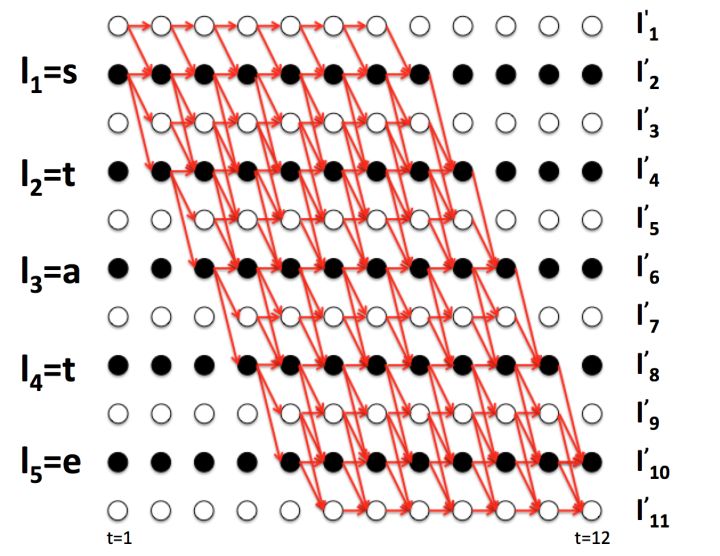
观察上图（（图源见参考资料[1]）可以发现，如果 t=6 时字符是 a，那么 t=5 时只能是字符 a，t，空白符三选一，否则经过 B 变换后无法得到 state。
可以得到以下递推关系：

α6(a)\=(α5(a)+α5(t)+α5(−))⋅ya6

更一般地，可以得到如下递推关系：

αt(lk′)\=(αt−1(lk′)+αt−1(lk−1′)+αt−1(−))⋅ylk′t

定义 backward为为βt(s)，表示 t 时刻经过 lk′字符的路径概率中 t-T 的概率之和，式子定义如下。

βt(lk′)\=∑B(π)\=l,πt\=lk′∏t′\=tTyπt′t′

t=T 时，符号只能是空白符或 l|l′|−1，可以得到以下初始条件：

βT(−)\=yT−βT(l|l′|−1′)\=yl|l′|−1TβT(l|l′|−i)\=0,∀i>1

同理，可以得到如下递推关系：

βt(lk′)\=(βt+1(lk′)+βt+1(lk+1′)+βt+1(−))⋅ylk′t

根据 forward 和 backward 的式子定义，它们相乘可以得到：

αt(lk′)βt(lk′)\=∑B(π)\=l,πt\=lk′ylk′t∏t\=1Tyπtt

又因为 p(l|x) 对 lk′求导时，只跟那些πt\=lk′的路径有关，那么求导时（注意是求导时）可以简写如下式子：

p(l|x)\=∑B(π)\=l,πt\=lk′p(π|x)\=∑B(π)\=l,πt\=lk′∏t\=1Tyπtt

结合上面两式，得到：

p(l|x)\=∑B(π)\=l,πt\=lk′αt(lk′)βt(lk′)ylk′t

最后可以得到求导式（这里用 k 来表示字符，和 lk′的含义相同）：

∂p(l|x)∂ykt\=∂∑B(π)\=l,πt\=kαt(k)βt(k)ykt∂ykt

求导式里的 forward 和 backward 可以用前面的 dp 递推式计算出来，时间复杂度是 nT，相比于前面的指数复杂度 nT 大大减小了计算量。

这样对 LSTM 的输出 y 求导之后，再根据 y 对 LSTM 里面的权重参数 w 进行链式求导，就可以使用梯度下降的方法来更新参数了。

CTC 的预测

一种方法是 Best Path search。计算概率最大的一条输出序列（假设时间步独立，那么直接在每个时间步取概率最大的字符输出即可），但是这样没有考虑多个输出序列对应一个真实输出这件事，举个例子，[s,s,-]和[s,s,s]的概率比[s,t,a]低，但是它们的概率之和会高于[s,t,a]。

第二种方法是 Beam Search。假设指定 B=3，预测过程如下图所示（图源见参考资料[2]）。在第一个时间步选取概率最大的三个字符，然后在第二个时间步也选取概率最大的三个字符，两两组合（概率相乘）可以组合成 9 个序列，这些序列在 B 转换之后会得到一些相同输出，把具有相同输出的序列进行合并，比如有 3 个序列都可以转换成 a，把它们合并（概率加在一起），计算出概率最大的三个序列，然后继续和下一个时间步的字符进行同样的合并。

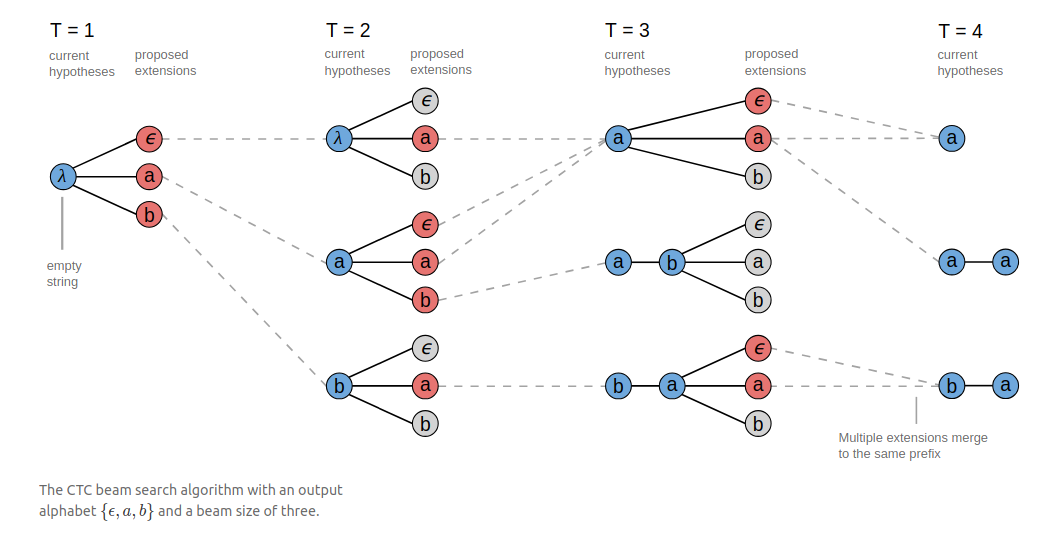
有一点需要注意的是合并相同字符时，比如我们看上图 T=3 的时候，第一个前缀序列 a，在跟相同字符 a 合并的时候，除了产生 a 之外，还会产生一个 aa 的有效输出。这是因为这个前缀序列 a 在 T=2 的时候曾经是把空白符合并掉了，实际上这个前缀序列 a 后面是跟着一个空白符的，所以它在跟相同字符 a 合并的时候中间是有一个隐藏的空白符，合并之后得到的应该是两个 a。

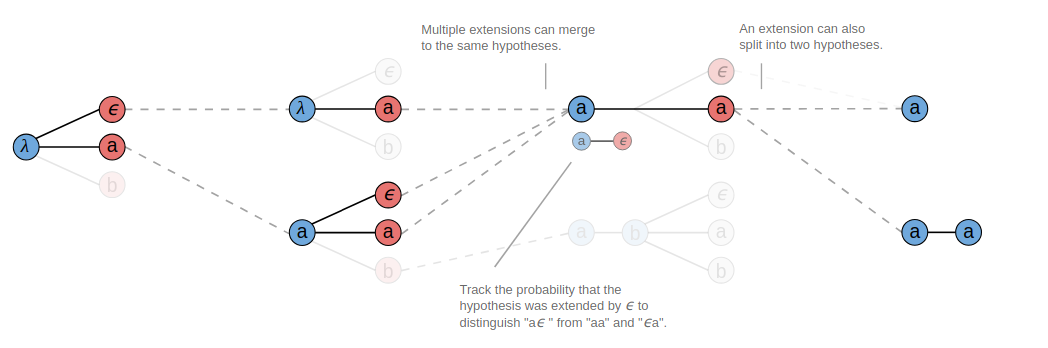
因此在合并相同字符时，如果要合并成 aa，需要统计在这之前以空白符结尾的那些序列的概率，如果要合并成 a，计算的是不以空白符结尾的那些序列的概率。出于这个事实，我们需要跟踪前两处输出，以便于后续的合并计算，见下图所示（图源见参考资料[2]）。

CTC 的几个性质

第一个是条件独立性。CTC 做了一个假设就是不同时间步的输出之间是独立的。这个假设对于很多序列问题来说并不成立，输出序列之间往往存在联系。

第二个是单调对齐。CTC 只允许单调对齐，在语音识别中可能是有效的，但是在机器翻译中，比如目标语句中的一些比较后的词，可能与源语句中前面的一些词对应，这个 CTC 是没法做到的。

第三个是多对一映射。CTC 的输入和输出是多对一的关系。这意味着输出长度不能超过输入长度，这在手写字体识别或者语音中不是什么问题，因为通常输入都会大于输出，但是对于输出长度大于输入长度的问题 CTC 就无法处理了。

参考资料

[1] 知乎上的一篇文章：一文读懂 CRNN+CTC 文字识别

[2] Distill 上一篇关于 CTC 的介绍（作者 Hannun Awni）：Sequence Modeling With CTC
https://www.cnblogs.com/liaohuiqiang/p/9953978.html