博客:blog.shinelee.me | 博客园 | CSDN
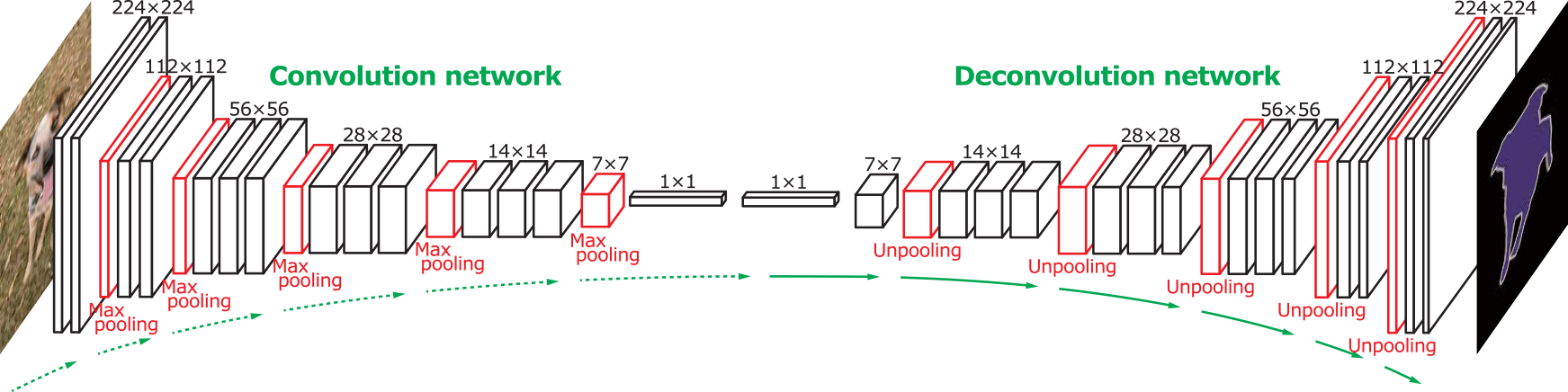
开篇先上图,图为deconvolution在像素级语义分割中的一种应用,直观感觉 deconvolution 是一个 upsampling 的过程,像是 convolution 的对称过程。
本文将深入 deconvolution 的细节,并通过如下方式展开:
- 先回答 什么是deconvolution?为什么会有transposed convolutionon、subpixel or fractional convolution这样的名字?
- 再介绍 各种情形下 transposed convolution是如何进行的,并提供一种统一的计算方法。
首先要明确的是,deconvolution 并不是个好名字,因为它存在歧义:
- deconvolution最初被定义为 “inverse of convolution” 或者 “inverse filter” 或者“解卷积”,是指消除先前滤波作用的方法。比如,我们认为原始图像是清晰的,但是通过透镜观测到的图像却变得模糊,如果假设透镜的作用相当于以某个 kernel 作用在原始图像上,由此导致图像变得模糊,那么根据模糊的图像估计这个 kernel 或者根据模糊图像恢复原始清晰图像的过程就叫deconvolution。
- 后来论文Adaptive Deconvolutional Networks for Mid and High Level Feature Learning和Visualizing and Understanding Convolutional Networks又重新定义了deconvolution,实际上与 transposed convolution、sub-pixel or fractional convolution 指代相同。transposed convolution是一个更好的名字,sub-pixel or fractional convolution 可以看成是 transposed convolution 的一个特例。对一个常规的卷积层而言,前向传播时是 convolution,将 input feature map 映射为 output feature map,反向传播时则是 transposed convolution,根据 output feature map 的梯度计算出 input feature map 的梯度,梯度图的尺寸与 feature map 的尺寸相同。
本文谈论的是 deconvolution 的第 2 个含义,后面统一使用transposed convolution这个名字。
什么是 transposed convolution?A guide to convolution arithmetic for deep learning中有这样一段话:

看完好像仍不是很直观,transposed convolution 到底对应的是什么操作?等到文章的后面,这个问题的答案会逐渐清晰起来。
下面先以 1 个例子来对比 convolution 过程和 transposed convolution 过程,采用与A guide to convolution arithmetic for deep learning相同的设置:
- 2-D transposed convolutions (N\=2 N=2)
- square inputs (i1\=i2\=i i_1=i_2=i)
- square kernel size (k1\=k2\=k k_1=k_2=k)
- same strides along both axes (s1\=s2\=s s_1=s_2=s)
- same zero padding along both axes (p1\=p2\=p p_1=p_2=p)
- square outputs (o1\=o2\=o o_1=o_2=o)
若令 i\=4 i=4、s\=1 s=1、p\=0 p=0、k\=3 k=3,输出尺寸 o\=2 o=2,则 convolution 过程是将 4×4 4\times 4 的 map 映射为 2×2 2\times 2 的 map,而 transposed convolution 过程则是将 2×2 2\times 2 的 map 映射为 4×4 4\times 4 的 map,两者的 kernel size 均为 3,如下图所示:
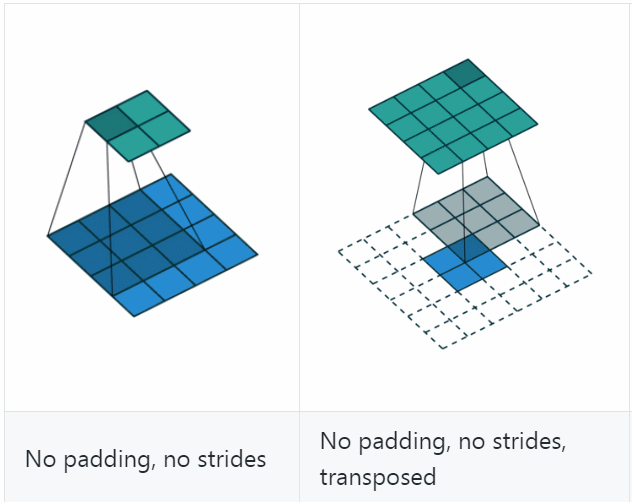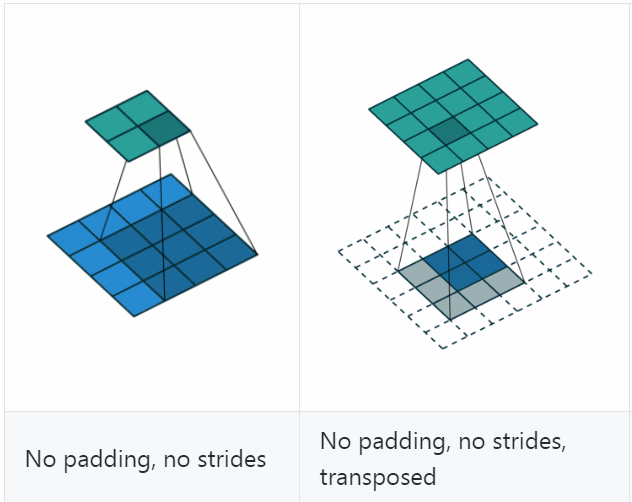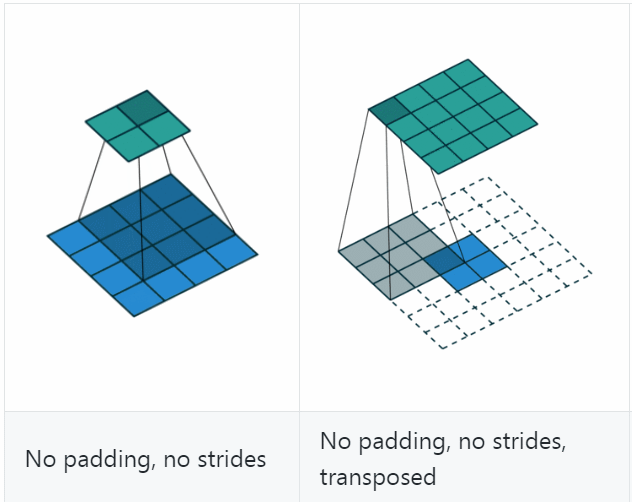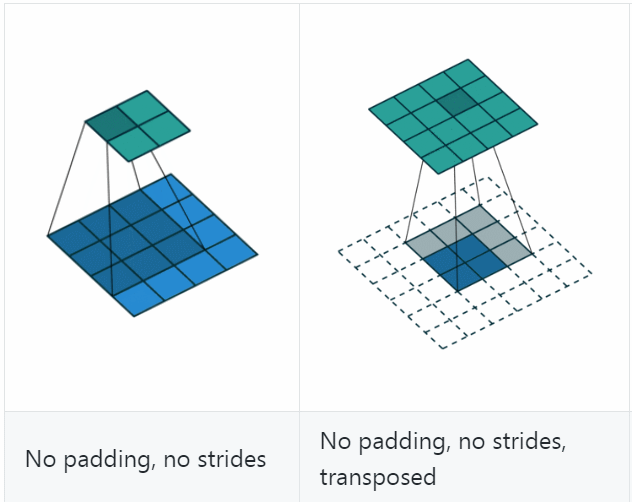
可以看到,convolution 过程 zero padding 的数量与超参数 p p 一致,但是 transposed convolution 实际的 zero padding 的数量为 2,为什么会这样?是为了保持连接方式相同,下面具体看一下。
convolution 过程
先看 convolution 过程,连接方式 如下图所示,绿色表示输出,蓝色表示输入,每个绿色块具与 9 个蓝色块连接。
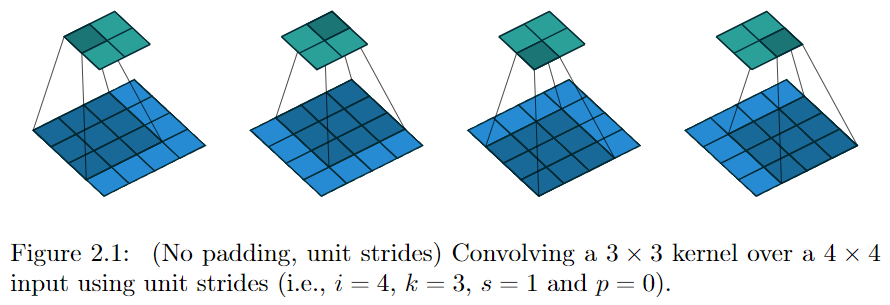
令卷积核 w\=(w0,0w0,1w0,2w1,0w1,2w1,2w2,0w2,1w2,2) \mathbf{w} = \left(\begin{array}{ccc} {w{0,0}} & {w{0,1}} & {w{0,2}} \ {w{1,0}} & {w{1,2}} & {w{1,2}} \ {w{2,0}} & {w{2,1}} & {w_{2,2}} \end{array}\right),为了便于理解,将卷积写成矩阵乘法形式,令 x \mathbf{x} 为 4×4 4\times 4 输入矩阵以行优先方式拉成的长度为 16 的向量,y \mathbf{y} 为 2×2 2\times 2 输出矩阵以同样方式拉成的长度为 4 的向量,同时将 w \mathbf{w} 表示成 4×16 4\times 16 的稀疏矩阵 C \mathbf{C},
C\=(w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,2000000w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,200000000w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,2000000w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,2) \mathbf{C} = \left(\begin{array}{cccccccccccccccc}{w{0,0}} & {w{0,1}} & {w{0,2}} & {0} & {w{1,0}} & {w{1,1}} & {w{1,2}} & {0} & {w{2,0}} & {w{2,1}} & {w{2,2}} & {0} & {0} & {0} & {0} & {0} \ {0} & {w{0,0}} & {w{0,1}} & {w{0,2}} & {0} & {w{1,0}} & {w{1,1}} & {w{1,2}} & {0} & {w{2,0}} & {w{2,1}} & {w{2,2}} & {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} & {w{0,0}} & {w{0,1}} & {w{0,2}} & {0} & {w{1,0}} & {w{1,1}} & {w{1,2}} & {0} & {w{2,0}} & {w{2,1}} & {w{2,2}} & {0} \ {0} & {0} & {0} & {0} & {0} & {w{0,0}} & {w{0,1}} & {w{0,2}} & {0} & {w{1,0}} & {w{1,1}} & {w{1,2}} & {0} & {w{2,0}} & {w{2,1}} & {w{2,2}}\end{array}\right)
则 convolution 过程可以描述为 Cx\=y \mathbf{C} \mathbf{x} = \mathbf{y},若Ci,j\=0 \mathbf{C}_{i,j}=0 表示 xj \mathbf{x}_j 和 yi \mathbf{y}_i 间没有连接。
transposed convolution 过程
再看 transposed convolution 过程,如何将长度为 4 的向量 y \mathbf{y} 映射为长度为 16 的向量且保持连接方式相同?只需将 C \mathbf{C} 转置,令 CTy\=x′ \mathbf{C}^T \mathbf{y} = \mathbf{x}’,同样地,Cj,iT\=0 \mathbf{C}^T_{j,i}=0 表示 xj′ \mathbf{x}’_j 和 yi \mathbf{y}_i 间没有连接。
此时,CT \mathbf{C}^T 对应的卷积操作恰好相当于将 kernel 中心对称,FULL zero padding,然后卷积,此时,1 个蓝色块与 9 个绿色块连接,且权重与 Convolution 过程相同
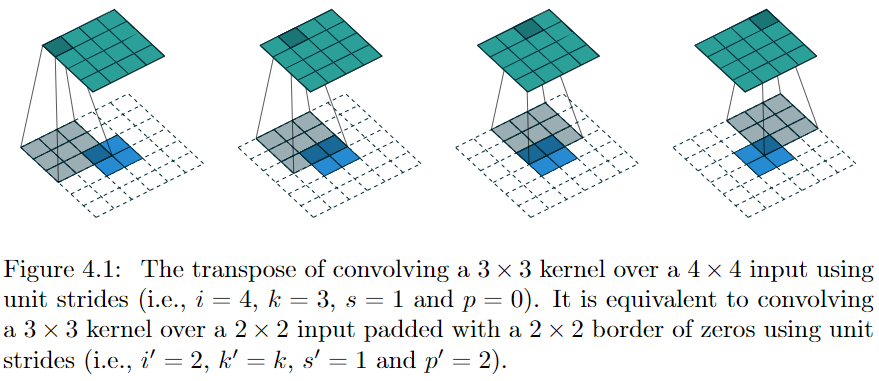
需要注意的是,transposed convolution 的 kernel 与 convolution 的 kernel 可以有关,也可以无关,需要看应用在什么场景,
- 在特征可视化、训练阶段的反向传播中应用的 transposed convolution,并不是作为一个真正的 layer 存在于网络中,其 kernel 与 convolution 共享(但要经过中心对称后再卷积,相当于上面的 $ \mathbf{C} ^T $)。
- 在图像分割、生成模型、decoder中使用的 transposed convolution,是网络中真实的 layer,其 kernel 经初始化后需要通过学习获得(所以卷积核也就无所谓中心对称不对称了)。
- 前向传播为 convolution/transposed convolution,则反向传播为 transposed convolution/convolution。
在上面举的简化的例子中,我们可以通过分析得知 transposed convolution 该如何进行,但是,对于更一般情况应该怎么做?
对于一般情况,只需把握一个宗旨:transposed convolution 将 output size 恢复为 input size 且保持连接方式相同。
对于 convolution 过程,我们知道其 output map 与 input map 的尺寸关系如下:
o\=⌊i+2p−ks⌋+1 o=\left\lfloor \frac{i+2p-k}{s} \right\rfloor + 1
若要将 o o 恢复为 i i,需考虑 2 种情况,i+2p−ks \frac{i+2p-k}{s} 整除以及不整除,先看整除的情况。
整除的情况
如果 i+2p−ks \frac{i+2p-k}{s} 可以整除,则由上式可得
i\=so−s+k−2p\=[o+(s−1)(o−1)]+(k−2p−1) i = so-s+k-2p = [o+(s-1)(o-1)]+(k-2p-1)
因为 transposed convolution 也是卷积,为了符合上面卷积操作尺寸关系的数学形式,可进一步整理成
i\=[o+(s−1)(o−1)]+[(k−1)+(k−2p−1)]−k1+1 i = \frac{[o+(s-1)(o-1)] + [(k-1)+(k-2p-1)] - k}{1} + 1
令 i′\=o+(s−1)(o−1) i’=o+(s-1)(o-1)、%2B(k-2p-1)%7D%7B2%7D%20%3D%20k-p-1%20%E3%80%81%20%E3%80%81s%E2%80%99%3D1%E3%80%81%20%E3%80%81k%E2%80%99%3Dk#card=math&code=p%E2%80%99%3D%5C%5Cfrac%7B%28k-1%29%2B%28k-2p-1%29%7D%7B2%7D%20%3D%20k-p-1%20%E3%80%81%20%E3%80%81s%E2%80%99%3D1%E3%80%81%20%E3%80%81k%E2%80%99%3Dk),即 transposed convolution 实际卷积时使用的超参数,可以这样理解:
i′\=o+(s−1)(o−1) i’=o+(s-1)(o-1):convolution 的输出为 o×o o\times o,每行每列都是 o o 个元素,有 o−1 o-1 个间隔,transposed convolution 时在每个间隔处插入 s−1 s-1 个 0,整体构成 transposed convolution 的 input map;
p′\=(k−1)+(k−2p−1)2\=k−p−1 p’=\frac{(k-1)+(k-2p-1)}{2} = k-p-1:在上一步 input map 的基础上再进行 padding,考虑 convolution 常用的几种 padding 情况:
- VALID:p\=0 p=0,transposed convolution 则需 padding p′\=k−1 p’=k-1,即FULL padding
- SAME:p\=k−12\=r p=\frac{k-1}{2}=r,这里考虑 k\=2r+1 k=2r+1 为奇数的一般情况,此时 p′\=r p’=r,即SAME padding
- FULL:p\=k−1 p=k-1,则 p′\=0 p’=0,即VALID padding
k′\=k k’=k:transposed convolution 的 kernel size 与 convolution 相同;
s′\=1 s’=1:transposed convolution 的 stride 均为 1,但也可以换个角度理解,如果认为 o×o o\times o 相邻元素间的距离为 1 个像素,那么在间隔处插入 s−1 s-1 个 0 后(s>1 s > 1),得到的 input map 相邻元素间的距离就是亚像素的(sub-pixel),所以此时也可以称之为 sub-pixel or fractional convolution;
o′\=i\=i′+2p′−k′s′+1 o’=i=\frac{i’+2p’-k’}{s’}+1:transposed convolution 的输出与 convolution 的输入具有相同尺寸。
不整除的情况
接下来再看 i+2p−ks \frac{i+2p-k}{s} 不整除的情况,此时再按上面的方式计算得到的 o′\=i′+2p′−k′s′+1 o’=\frac{i’+2p’-k’}{s’}+1 将小于 i i,小多少呢?不难得出少 a\=[(i+2p−k)mods] a = [(i+2p-k) \mod s],即
o′\=i′+2p′−k′s′+1\=i−a o’=\frac{i’+2p’-k’}{s’}+1=i-a
为了让 o′\=i o’=i,可写成
o′\=i′+2p′+a−k′s′+1 o’= \frac{i’+2p’+a-k’}{s’}+1
只需在 padding 后,在下边和右边再扩展 a a 行和列 0,然后进行卷积即可。注意,因为 s′\=1 s’=1,我们可以将 a a 放在分母也可以放在外面,之所以放在分母,是因为 convolution 过程中 input map 下边和右边的 a a 行或列中的元素可能参与了运算,即与 output map 间存在连接,所以在 transposed convolution 时,为了保持同样的连接,最后扩展的 a a 行和列也要参与卷积,所以放在分母。
至此,再看 transposed convolution 的各种情况,就很容易推算了,更多例子可参见A guide to convolution arithmetic for deep learning。
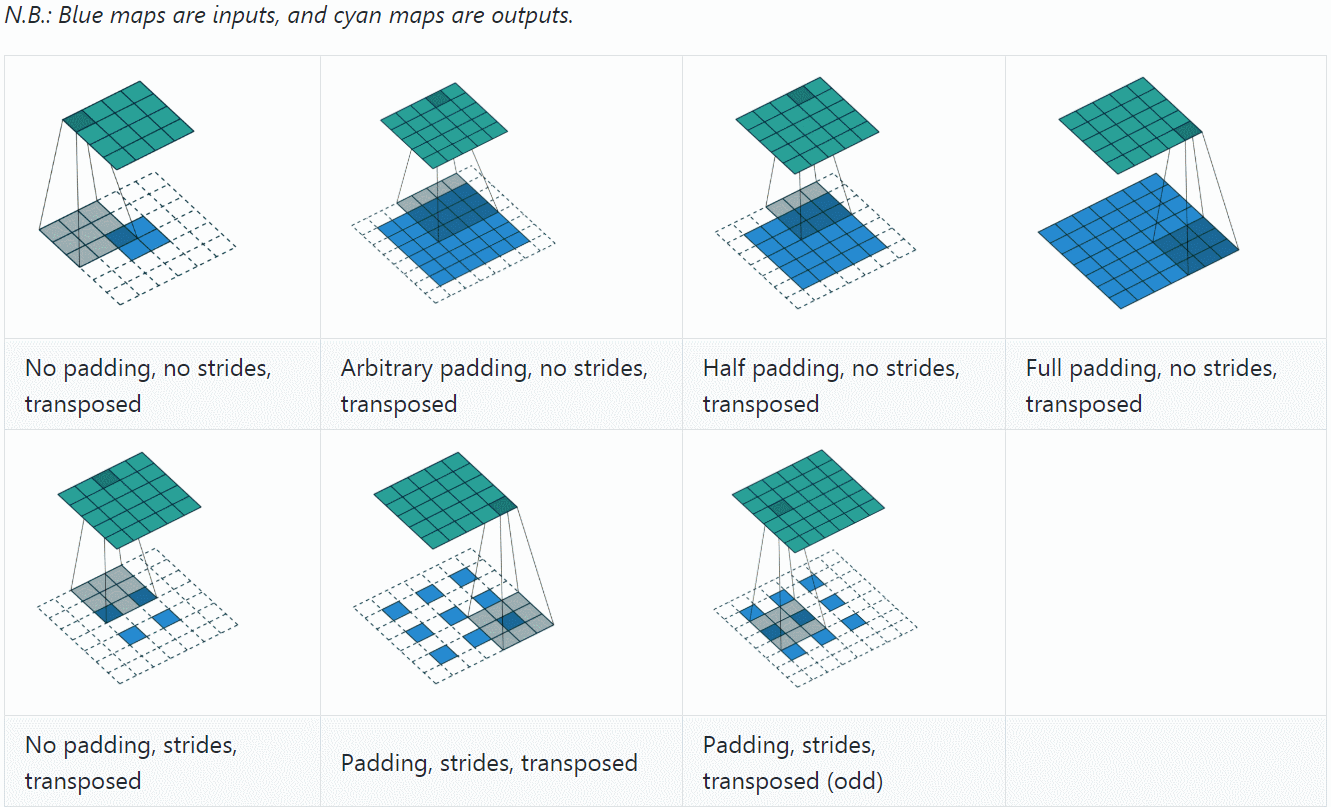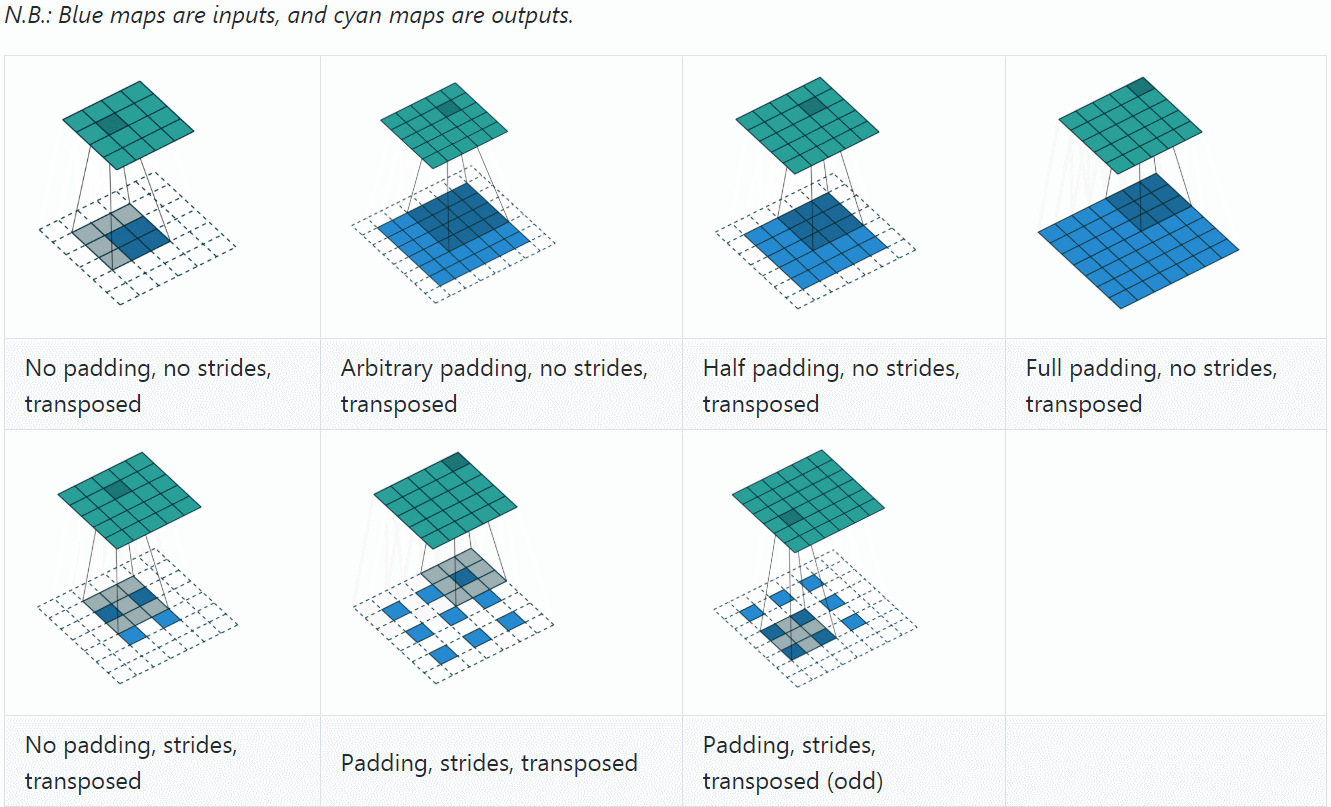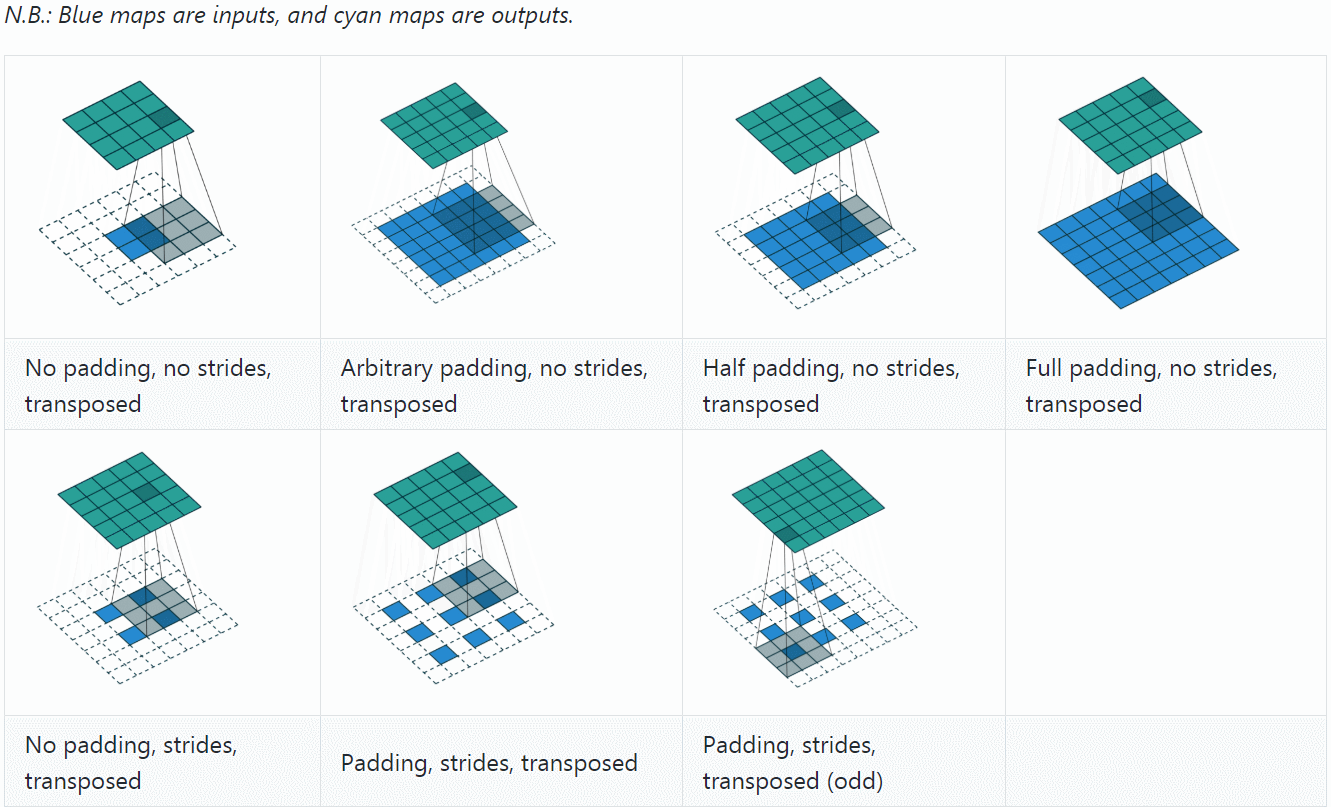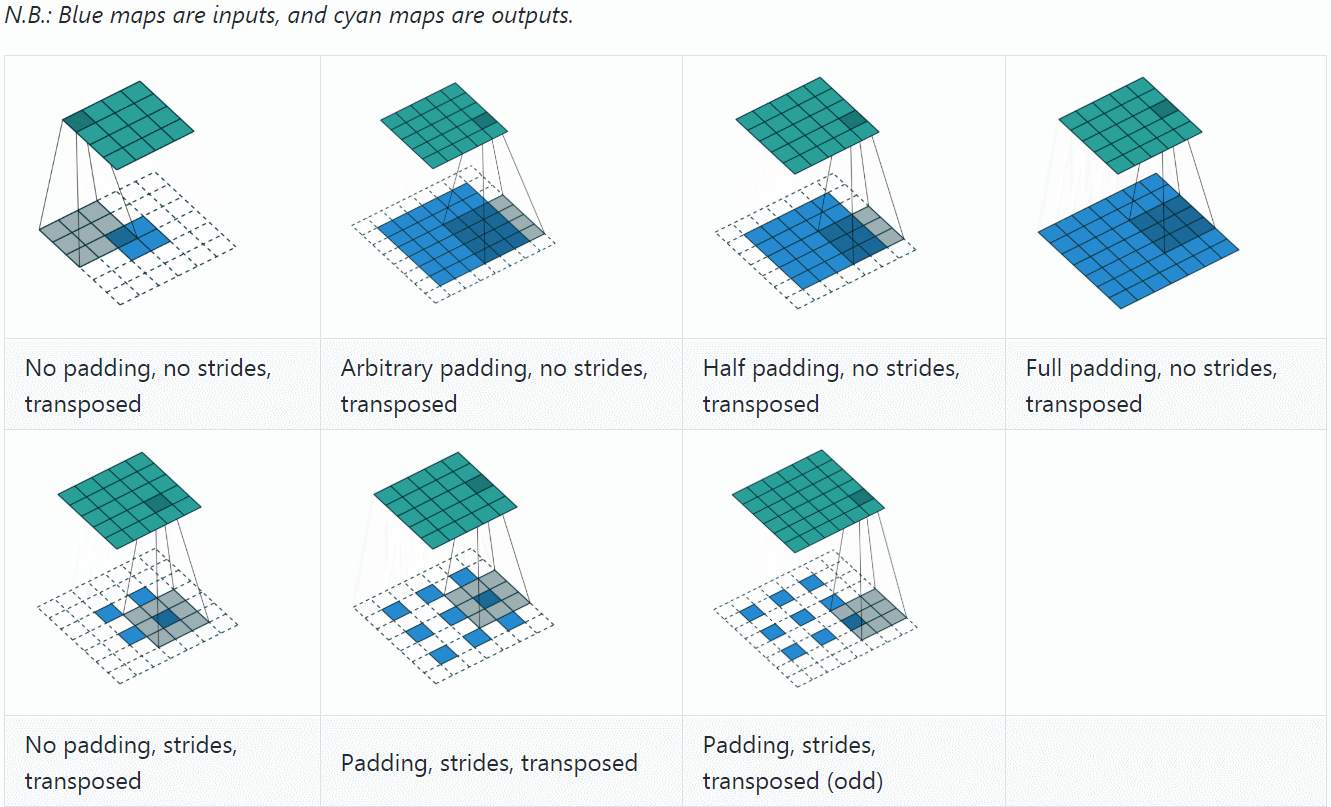
最后,总结一下,
convolution 和 transposed convolution 互为对称过程,存在一个 convolution,就存在一个与之对应的 transposed convolution,反之亦然;
convolution 是将 input size 的 map 映射为 output size 的 map,transposed convolution 是将 output size 的 map 映射为 input size 的 map——旨在将尺寸恢复;
两者均使用卷积操作,为了方便,两者使用同样的 stride、padding、kernel size 超参数,但实际执行时的操作不同,一般情况下,transposed convolution 与 convolution 实际超参数关系为:i′\=o+(s−1)(o−1) i’=o+(s-1)(o-1)、
%2B(k-2p-1)%7D%7B2%7D%20%3D%20k-p-1%20%E3%80%81%20%E3%80%81s%E2%80%99%3D1%E3%80%81%20%E3%80%81k%E2%80%99%3Dk#card=math&code=p%E2%80%99%3D%5C%5Cfrac%7B%28k-1%29%2B%28k-2p-1%29%7D%7B2%7D%20%3D%20k-p-1%20%E3%80%81%20%E3%80%81s%E2%80%99%3D1%E3%80%81%20%E3%80%81k%E2%80%99%3Dk)。
之所以做这样的操作,是为了保证 map 间的连接方式相同(权重不一定相同),权重的设置需根据应用的场景,可能通过学习得到,也可能与 convolution 共享(但需要中心对称后再使用)。
Is the deconvolution layer the same as a convolutional layer?
What are deconvolutional layers?
https://blog.csdn.net/blogshinelee/article/details/101078452

