反卷积(Transposed Convolution)详细推导 - 知乎

阅读本文的基础，是默认已经理解了图像处理中正向卷积的过程 (卷积特征提取 - UFLDL)。

什么是反卷积？

• 上采样 (Upsample)

在应用在计算机视觉的深度学习领域，由于输入图像通过卷积神经网络 (CNN) 提取特征后，输出的尺寸往往会变小，而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.: 图像的语义分割)，这个采用扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样(Upsample)。

• 反卷积 (Transposed Convolution)

上采样有 3 种常见的方法：双线性插值 (bilinear)，反卷积 (Transposed Convolution)，反池化 (Unpooling)，我们这里只讨论反卷积。这里指的反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：

反卷积是一种特殊的正向卷积，先按照一定的比例通过补
来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

反卷积的数学推导

• 正向卷积的实现过程

假设输入图像
尺寸为
，元素矩阵为：

卷积核
尺寸为
，元素矩阵为：

步长
，填充
，即
，

则按照卷积计算公式
，输出图像
的尺寸为
。

• 用矩阵乘法描述卷积

把
的元素矩阵展开成一个列向量
：

把输出图像
的元素矩阵展开成一个列向量
：

对于输入的元素矩阵
和 输出的元素矩阵
，用矩阵运算描述这个过程：

通过推导，我们可以得到稀疏矩阵
：

反卷积的操作就是要对这个矩阵运算过程进行逆运算，即通过
和
得到
，根据各个矩阵的尺寸大小，我们能很轻易的得到计算的过程，即为反卷积的操作：

但是，如果你代入数字计算会发现，反卷积的操作只是恢复了矩阵
的尺寸大小，并不能恢复
的每个元素值，本文最后会在 tensorflow 平台进行这个实验。

在此之前，我们先给出反卷积图像尺寸变化的公式。

• 反卷积的输入输出尺寸关系

在进行反卷积时，简单来说，大体上可分为以下两种情况：

Relationship 1：

此时反卷积的输入输出尺寸关系为：

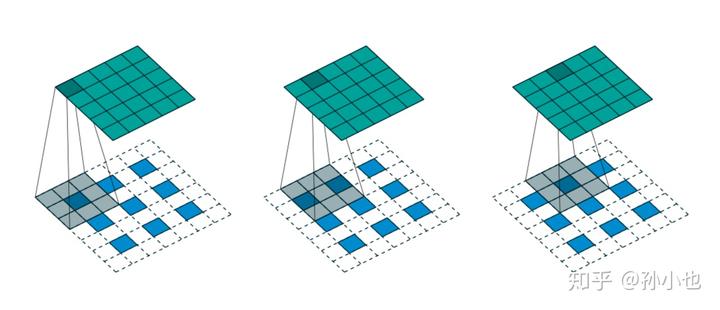
如上图所示，我们选择一个输入
尺寸为
，卷积核
尺寸为
，步长
，填充
，即
，则输出
的尺寸为
。

Relationship 2：

此时反卷积的输入输出尺寸关系为：

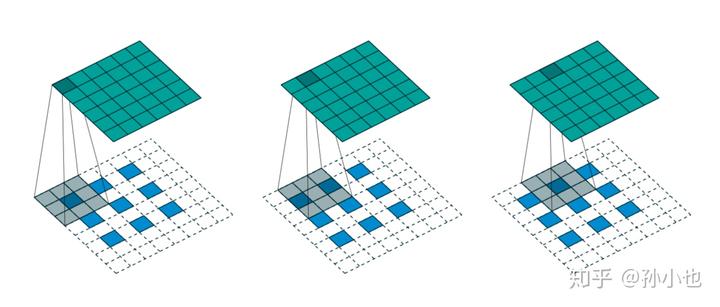
如上图所示，我们选择一个输入
的尺寸为
，卷积核
的尺寸为
，步长
，填充
，即
，则输出
的尺寸为
。

• 反卷积在 FCN 中的应用

在图像语义分割网络 FCN-32s 中，上采样反卷积操作的输入每张 {\E heatmap} 的尺寸是
，我们希望进行一次上采样后能恢复成原始图像的尺寸
，代入公式：

根据上式，我们可以得到一个关于
三者之间关系的等式：

通过实验，最终找出了最合适的一组数据：

在 tensorflow 中实现反卷积

• 反卷积的具体计算步骤

下面我们用一组实验更直观的解释一下在 tensorflow 中反卷积的过程：

我们令输入图像为：

卷积核为：

case 1

如果要使输出的尺寸是
，步数
，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input, 
                                        filter=kernel, 
                                        output_shape=[1,5,5,1], 
                                        strides=2, 
                                        padding='SAME')

当执行 transpose_conv 命令时，tensorflow 会先计算卷积类型、输入尺寸、步数和输出尺寸之间的关系是否成立，如果不成立，会直接提示错误，如果成立，执行如下操作：

1. 现根据步数
   对输入的内部进行填充，这里
   可以理解成输入放大的倍数，即在
   的每个元素之间填充
   ，
   的个数
   与
   的关系为：

例如这里举例的
，即在
的每个元素之间填
个
：

因为卷积类型为 same，所以此时，
。

1. 接下来，用卷积核
   对填充后的输入
   进行步长
   的正向卷积，根据正向卷积输出尺寸公式：
   得到输出尺寸是
   ，反卷积公式中我们给出的输出尺寸参数
   也是为
   ，两者相同，所以可以进行计算，结果为：

与 tensorflow 的运行结果相同。

case 2

我们将 case 1 中的输出尺寸
改成
，其他参数均不变，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input, 
                                        filter=kernel, 
                                        output_shape=[1,6,6,1], 
                                        strides=2, 
                                        padding='SAME')

卷积类型是 same，我们首先在外围填充一圈
：

这时发现，填充后的输入尺寸与
的卷积核卷积后的输出尺寸是
，没有达到
的
，这就需要继续填充
，tensorflow 的计算规则是优先在左侧和上侧填充一排
，填充后的输入变为：

接下来，再对这个填充后的输入与
的卷积核卷积，结果为：

与 tensorflow 的运行结果相同。

• 反卷积只能恢复尺寸，不能恢复数值

最后，我们要验证一下前文中提到的 “如果你代入数字计算会发现，反卷积的操作只是恢复了矩阵
的尺寸大小，并不能恢复
的每个元素值”。

1. 正向卷积：
   value = tf.reshape(tf.constant([[1., 2., 3.],
   [4., 5., 6.],
   [7., 8., 9.]]),
   [1, 5, 5, 1])
   filter = tf.reshape(tf.constant([[1., 0.],
   [0., 1.]]),
   [2, 2, 1, 1])
   output = tf.nn.conv2d(value, filter, [1, 2, 2, 1], ‘SAME’)

卷积的结果是：

1. 我们用和正向卷积完全相同的参数对这个结果进行反卷积：
   input = tf.reshape(tf.constant([[6., 8., 3.],
   [12., 14., 6.],
   [7., 8., 9.]]),
   [1, 3, 3, 1])
   kernel = tf.reshape(tf.constant([[1., 0.],
   [0., 1.]]),
   [2, 2, 1, 1])
   output = tf.nn.conv2d_transpose(value=input,
   filter=kernel,
   output_shape=[1, 3, 3, 1],
   strides=[1, 2, 2, 1],
   padding=’SAME’)

卷积的结果是：

可见，反卷积不能恢复数值，而且，在当
时，即便使用完全相同的参数进行转置卷积，输入的尺寸也不能恢复。

参考文献

Dumoulin V, Visin F. A guide to convolution arithmetic for deep learning[J]. arXiv preprint arXiv:1603.07285, 2016.
https://zhuanlan.zhihu.com/p/48501100