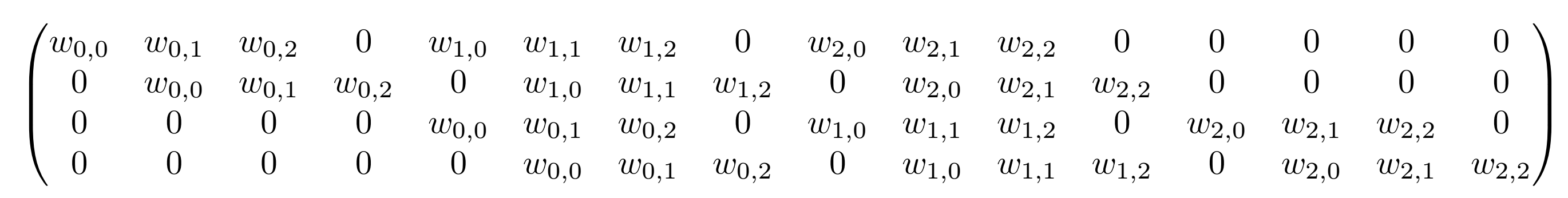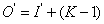A guide to convolution arithmetic for deep learning学习笔记
A guide to convolution arithmetic for deep learning学习笔记—-
1.综述
本文章是对深度学习中出现的各种类型的卷积进行汇总。
https://github.com/vdumoulin/conv_arithmetic
文章主要关注两个方面：一是卷积层和转秩卷积层之间的关系；二是对卷积层、池化层和转秩卷积层中input,kernel,padding,stride,output的尺寸提供直观的理解。
离散卷积：
卷积神经网络的基本组成是仿射变换，f(wx+b)。图像、语音或者其他无序的特征组合都可以作为卷积的输入，一般是先将其变成一个向量。但图像、语音和其他相似数据都有固定的结构，他们存在一些共有属性：保存成多维数组的形式；某些象限按序保存数据；另外有一个象限来获取不同视角的数据。使用仿射变化处理上述数据时，所有的数据都以相同的方式进行处理，没有利用数据本身的拓扑信息。在图像处理和语音识别领域，利用数据的内部结构是非常有益的，所以这就是为什么要利用离散卷积的原因。
离散卷积是一种保持了数据本身顺序的线性变换，两个关键特性：稀疏连接和权值共享能够减少参数数量，防止过拟合。
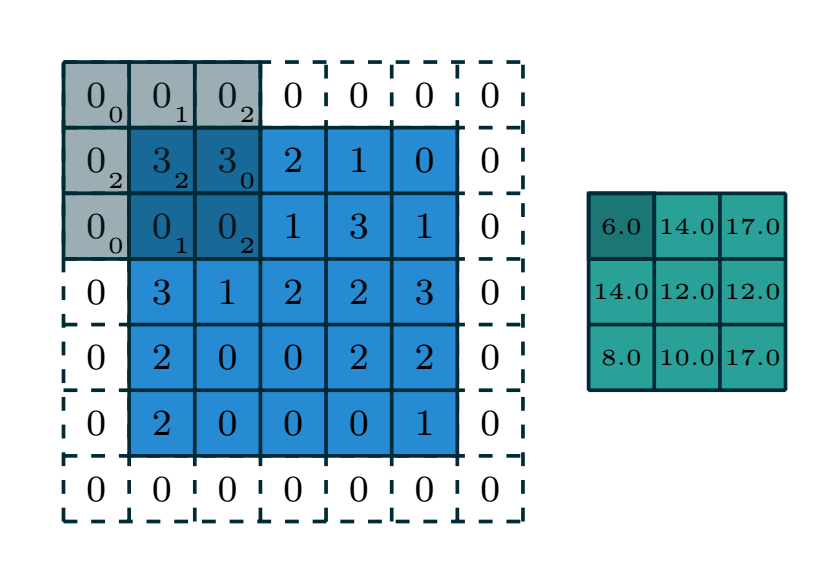
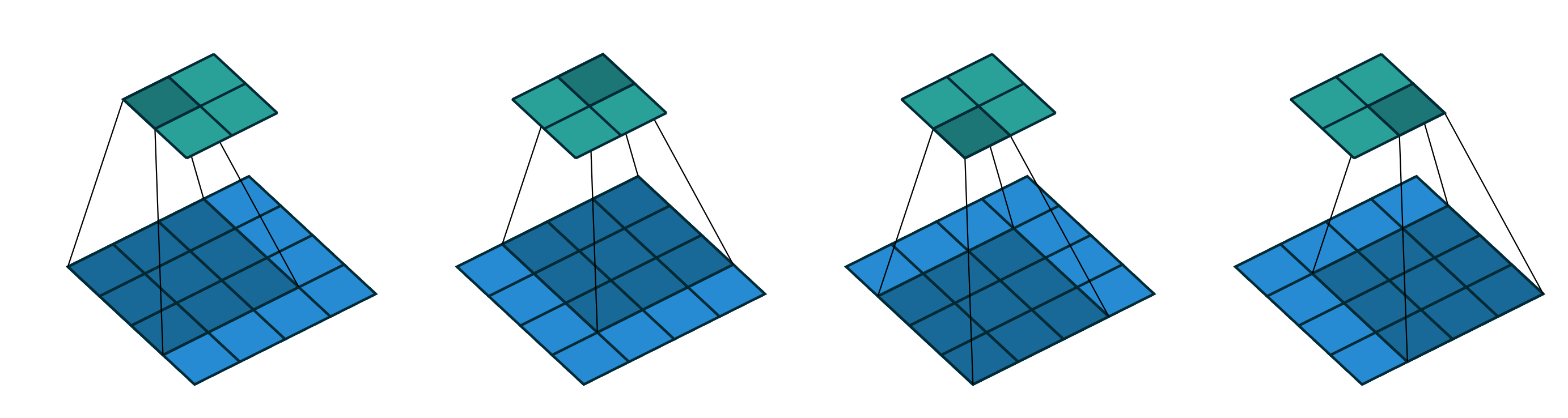
离散卷积的实现过程包括了input feature map、kernel、output feature map，卷积核按照一定的stride值在输入feature map上进行滑动，在每一位置，计算卷积核和覆盖的input feature map对应位置的元素乘积再求和，作为该处的output feature map的值。二维卷积如下图所示，给出了计算output feature map的第一个值6.0的计算过程。
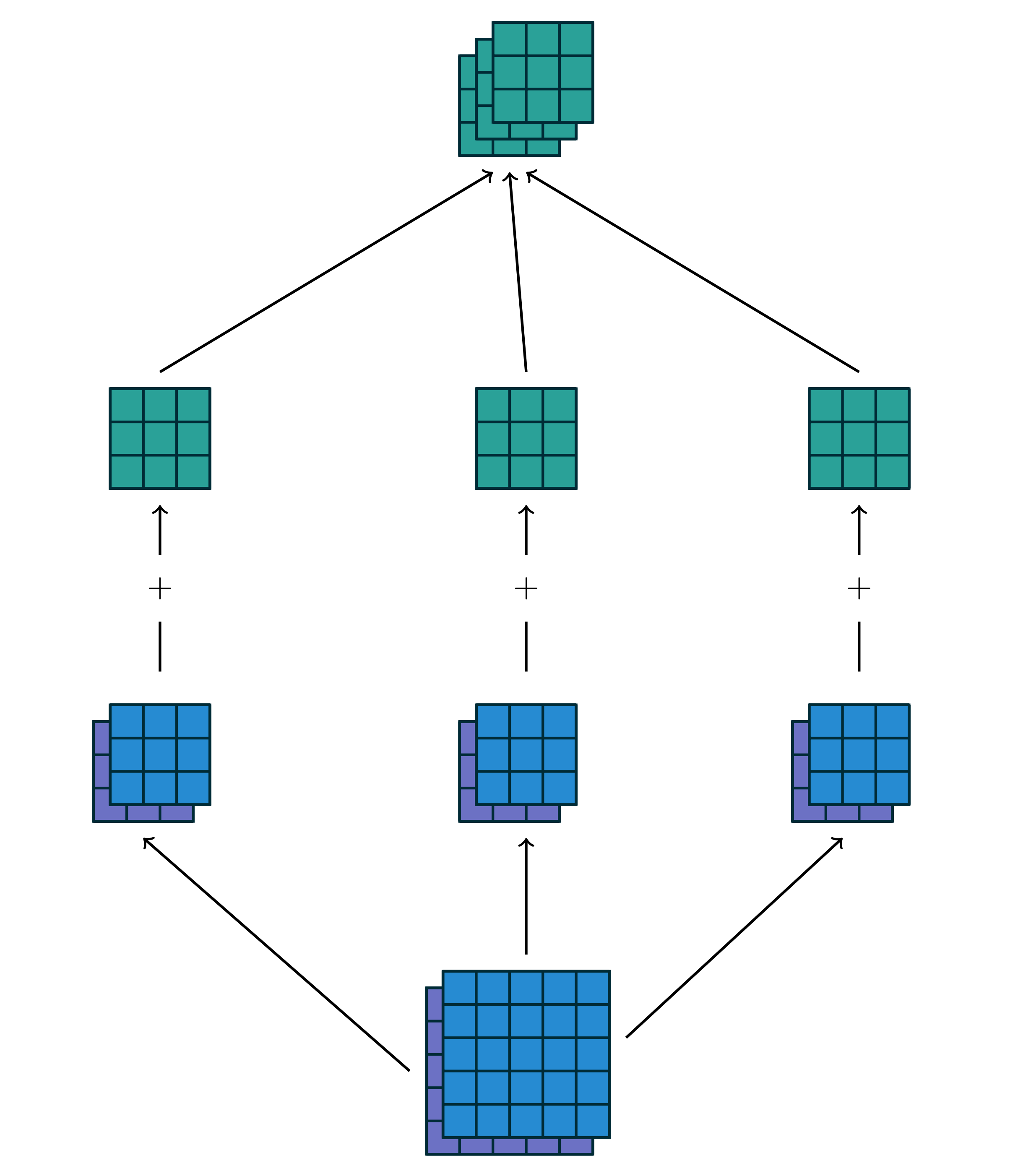
如果input feature map有多个通道，那么kernel就需要有相同数量的通道，在卷积过程中，kernel和input feature map相同的channel进行元素相乘再求和(求和是先各channel对应元素相乘结果求和，然后再是各channel的求和结果再求和，最终得到的是一个数值)。如下图所示，输入为255，卷积核为3233，表示共有三个不同的卷积核，每个卷积核2个通道(和输入的通道数相同)，每个通道的卷积核大小为33，卷积完成之后得到的输出为333，表示3个卷积核分别得到了卷积结果，每个卷积结果的尺寸为3*3.
决定卷积之后output feature map尺寸的因素包括：input feature map的尺寸，kernel的尺寸，stride的大小和zero padding的大小。
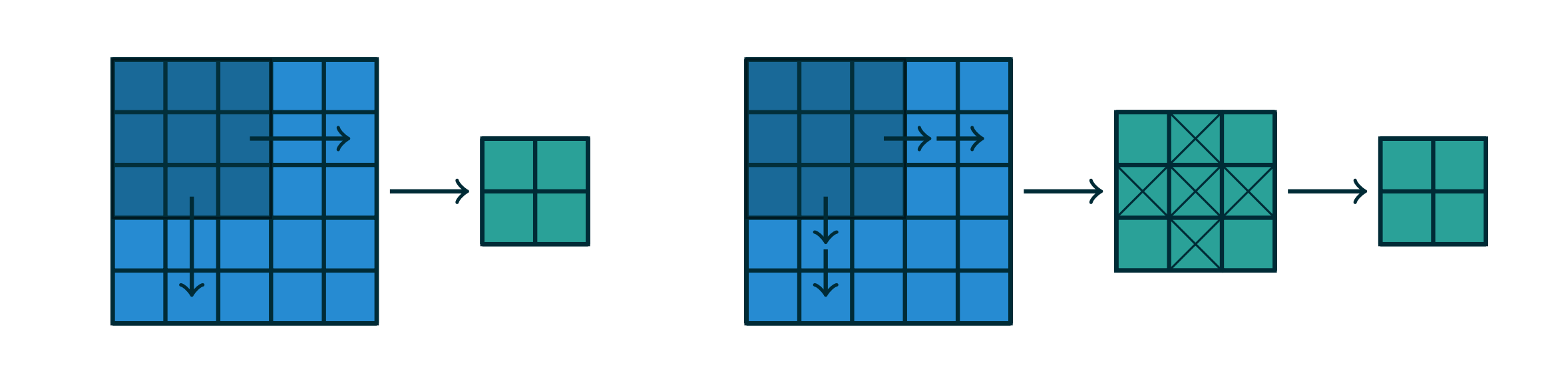
stride可以理解成卷积核滑动步长的大小，也可以理解成一种二次采样的形式，可以理解成按照stride=1进行卷积之后再进行采样的过程。如下图右侧所示，stride=2可以理解成先按照stride=1进行卷积之后只保留奇数位置的值。
池化：
池化是卷积神经网络的另一个重要组成部分，池化是对图像的子块进行操作，常用的池化有平均池化和最大池化两种。平均池化是取子块的均值作为输出结果，最大池化则是取子块的最大值作为输出结果。池化输出的尺寸由输入尺寸、kernel大小和stride值的大小决定。
2.卷积
输入的尺寸为i，卷积核大小为k，stride的大小为s，padding的大小为p，输出的尺寸为o，只考虑卷积核和输入的x和y相等的情况。
2.1 不补0，stride为1的卷积
o = (i - k) + 1
2.2 补0，stride为1的卷积
o = (i - k) + 2p + 1
2.2.1 half(same) padding
这种方式的卷积要进行padding，并且目的是保证输出和输入具有相同的尺寸。由于卷积过程中使用的卷积核一半大小为奇数，所以为了保证
(i-k)+2p+1 = i,则p=(k-1)/2=(k/2)的向下取整。
2.2.2 full padding
padding的大小为k-1.
2.3 不补0，stride不为1
o = ((i-k)/s)向下取整 + 1
2.4 补0，stride不为1
o = ((i-k+2*p)/s)向下取整 + 1
3.池化
池化层为神经网络提供了对小范围平移的不变性，以最大池化为例，对图像进行小范围平移之后，如果平移量小于池化区域的大小，那么平移前后该区域得到了相同的池化结果，因此具有了平移不变性。
o = ((i - k) / s)向下取整 + 1
4.转秩卷积
转秩卷积是卷积的逆变换过程，是根据输出来推导输入。很多地方把根据输出推输入的过程叫做逆卷积，这个名字容易误导，真实的过程是转秩卷积。
转秩卷积也不会跨通道进行计算。
4.1 卷积就是一个矩阵乘积的过程
把卷积核扩充为416的矩阵C，图像展开成116的向量，矩阵乘之后得到41的向量，再变换成22的输出。卷积的计算过程就是O = C I。那么反向计算的时候，是根据O来计算I，就是 I = C的转秩 O.
4.2 转秩卷积
转秩卷积过程正向时左乘C的转秩；反向时乘C的转秩的转秩，也就是左乘C。
4.3 不补0，stride为1的转秩卷积
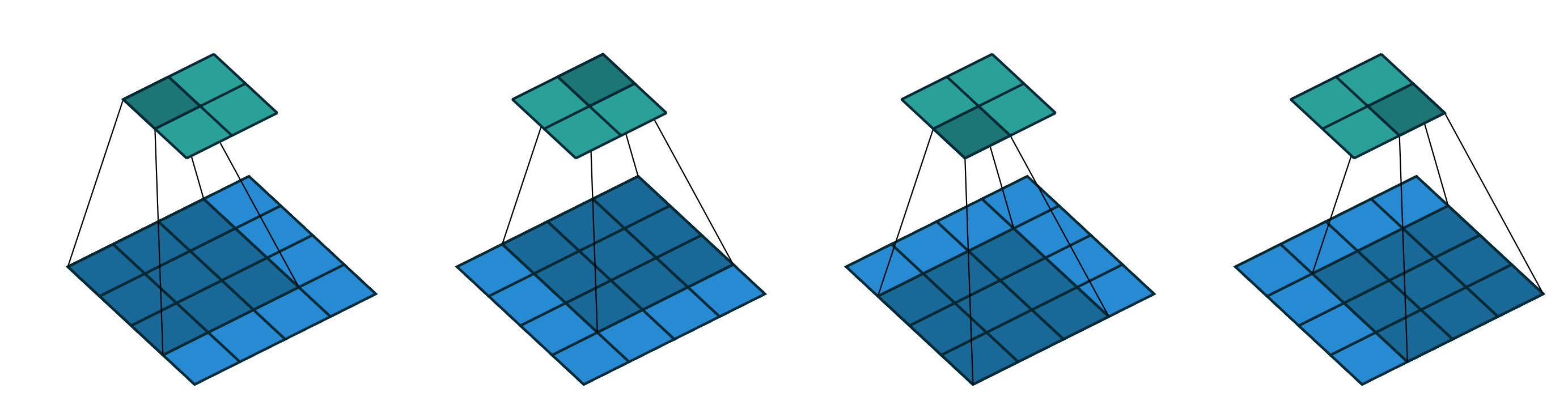
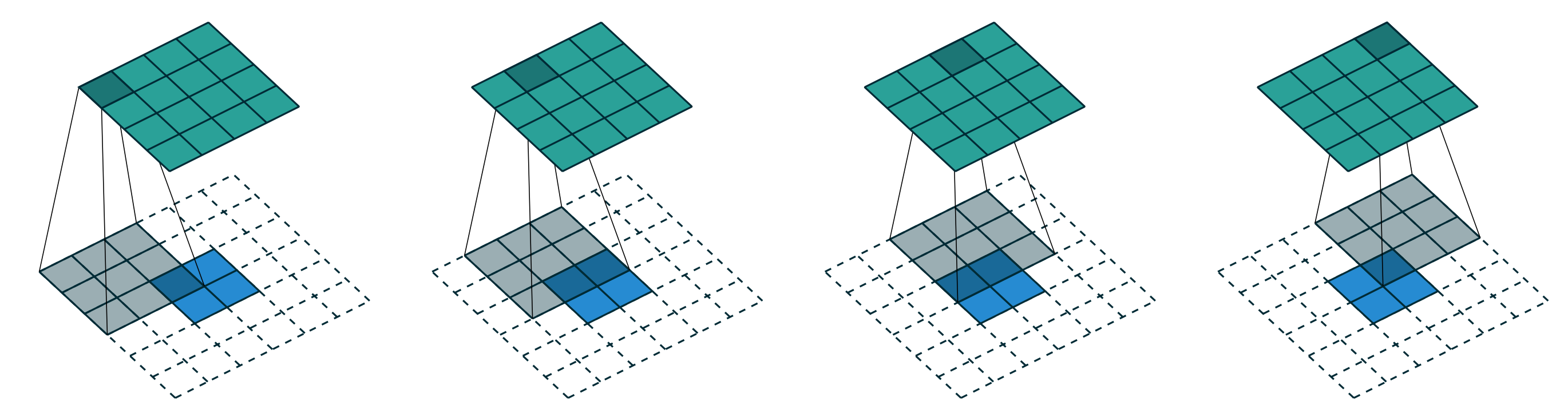
计算转秩卷积的过程可以是对输入进行补0扩充，之所以这样做是因为正向卷积的过程中，输入的最左上角的元素只对输出的左上角元素有贡献，而输入的第一行第二列的元素则对输出的第一行的两个元素都有贡献。那么在转秩卷积的过程中，输入只需要对输出的最左上角的元素有贡献即可，而输入的第一行第二列的元素则需要对输出的第一行第一列和第一行第二列的两个元素都有贡献。以此类推，可以得到转秩卷积时要对输入进行padding为2的补0操作。
下面是各种类型的转秩卷积如何补0，输出与输入的计算公式。
若有收获，就点个赞吧
0 人点赞
