参考：
https://zhuanlan.zhihu.com/p/28749411
https://zhuanlan.zhihu.com/p/28186857
https://blog.yani.io/filter-group-tutorial/
https://www.zhihu.com/question/54149221
http://blog.csdn.net/guvcolie/article/details/77884530?locationNum=10&fps=1
http://blog.csdn.net/zizi7/article/details/77369945
https://github.com/vdumoulin/conv_arithmetic
https://www.zhihu.com/question/43609045/answer/130868981

在可分离卷积（separable convolution）中，通常将卷积操作拆分成多个步骤。而在神经网络中通常使用的就是深度可分离卷积（depthwise separable convolution）。
举个例子，假设有一个 3×3 大小的卷积层，其输入通道为 16、输出通道为 32。
那么一般的操作就是用 32 个 3×3 的卷积核来分别同输入数据卷积，这样每个卷积核需要 3×3×16 个参数，得到的输出是只有一个通道的数据。之所以会得到一通道的数据，是因为刚开始 3×3×16 的卷积核的每个通道会在输入数据的每个对应通道上做卷积，然后叠加每一个通道对应位置的值，使之变成了单通道，那么 32 个卷积核一共需要 (3×3×16)×32 =4068 个参数。

1.1 标准卷积与深度可分离卷积的不同

用一张来解释深度可分离卷积，如下：
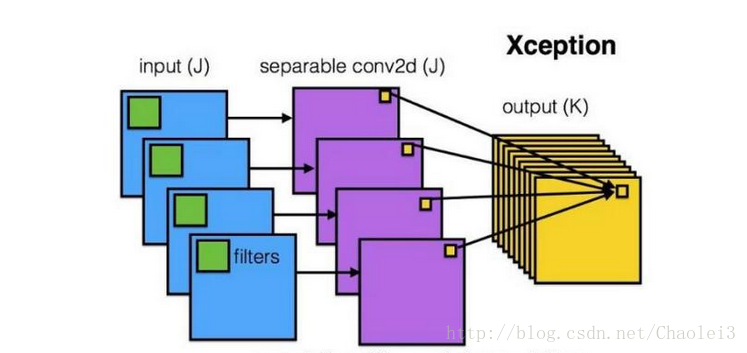
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图1

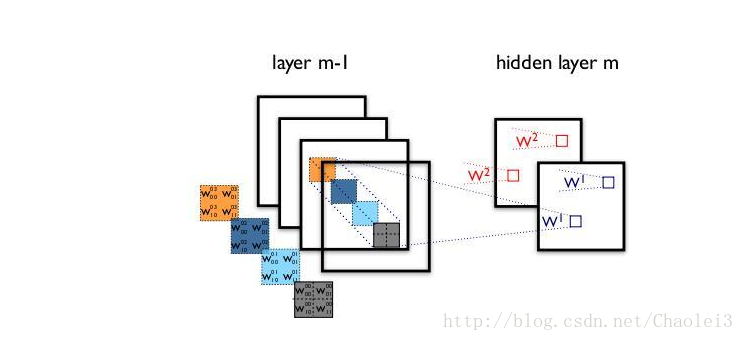
可以看到每一个通道用一个 filter 卷积之后得到对应一个通道的输出，然后再进行信息的融合。而以往标准的卷积过程可以用下面的图来表示：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图2

1.2 深度可分离卷积的过程

而应用深度可分离卷积的过程是①用 16 个 3×3 大小的卷积核（1 通道）分别与输入的 16 通道的数据做卷积（这里使用了 16 个 1 通道的卷积核，输入数据的每个通道用 1 个 3×3 的卷积核卷积），得到了 16 个通道的特征图，我们说该步操作是 depthwise（逐层）的，在叠加 16 个特征图之前，②接着用 32 个 1×1 大小的卷积核（16 通道）在这 16 个特征图进行卷积运算，将 16 个通道的信息进行融合（用 1×1 的卷积进行不同通道间的信息融合），我们说该步操作是 pointwise（逐像素）的。这样我们可以算出整个过程使用了 3×3×16+（1×1×16）×32 =656 个参数。

1.3 深度可分离卷积的优点

可以看出运用深度可分离卷积比普通卷积减少了所需要的参数。重要的是深度可分离卷积将以往普通卷积操作同时考虑通道和区域改变成，卷积先只考虑区域，然后再考虑通道。实现了通道和区域的分离。

Group convolution 分组卷积，最早在 AlexNet 中出现，由于当时的硬件资源有限，训练 AlexNet 时卷积操作不能全部放在同一个 GPU 处理，因此作者把 feature maps 分给多个 GPU 分别进行处理，最后把多个 GPU 的结果进行融合。

2.1 什么是分组卷积

在说明分组卷积之前我们用一张图来体会一下一般的卷积操作。
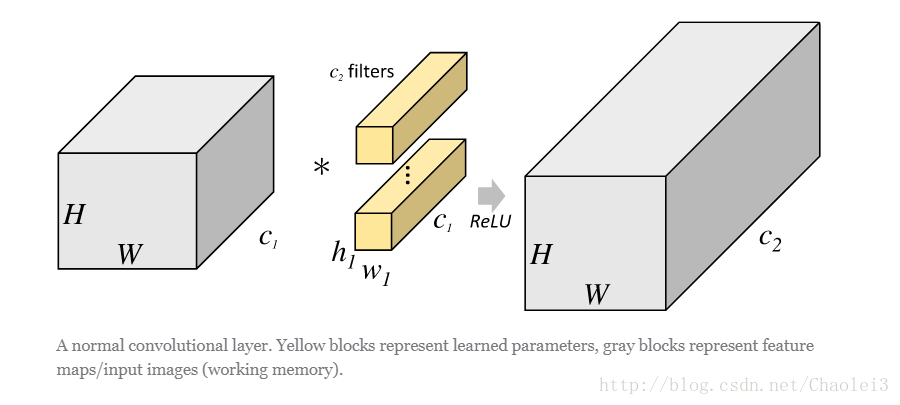
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图3

从上图可以看出，一般的卷积会对输入数据的整体一起做卷积操作，即输入数据：H1×W1×C1；而卷积核大小为 h1×w1，一共有 C2 个，然后卷积得到的输出数据就是 H2×W2×C2。这里我们假设输出和输出的分辨率是不变的。主要看这个过程是一气呵成的，这对于存储器的容量提出了更高的要求。
但是分组卷积明显就没有那么多的参数。先用图片直观地感受一下分组卷积的过程。对于上面所说的同样的一个问题，分组卷积就如下图所示。
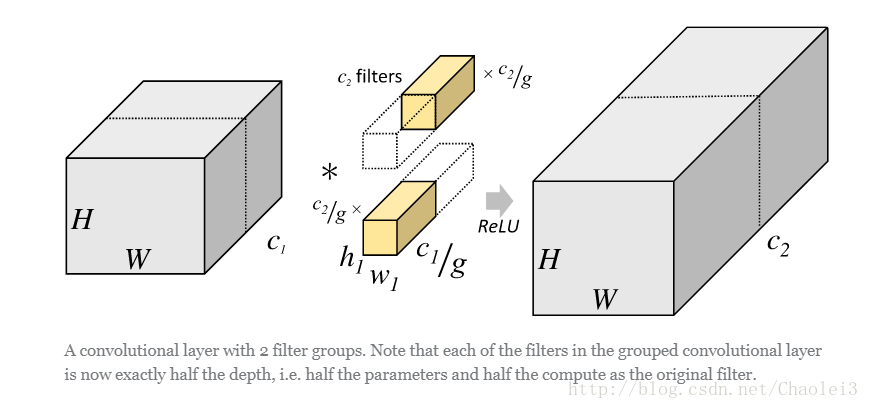
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图4

可以看到，图中将输入数据分成了 2 组（组数为 g），需要注意的是，这种分组只是在深度上进行划分，即某几个通道编为一组，这个具体的数量由（C1/g）决定。因为输出数据的改变，相应的，卷积核也需要做出同样的改变。即每组中卷积核的深度也就变成了（C1/g），而卷积核的大小是不需要改变的，此时每组的卷积核的个数就变成了（C2/g）个，而不是原来的 C2 了。然后用每组的卷积核同它们对应组内的输入数据卷积，得到了输出数据以后，再用 concatenate 的方式组合起来，最终的输出数据的通道仍旧是 C2。也就是说，分组数 g 决定以后，那么我们将并行的运算 g 个相同的卷积过程，每个过程里（每组），输入数据为 H1×W1×C1/g，卷积核大小为 h1×w1×C1/g，一共有 C2/g 个，输出数据为 H2×W2×C2/g。

2.2 分组卷积具体的例子

从一个具体的例子来看，Group conv 本身就极大地减少了参数。比如当输入通道为 256，输出通道也为 256，kernel size 为 3×3，不做 Group conv 参数为 256×3×3×256。实施分组卷积时，若 group 为 8，每个 group 的 input channel 和 output channel 均为 32，参数为 8×32×3×3×32，是原来的八分之一。而 Group conv 最后每一组输出的 feature maps 应该是以 concatenate 的方式组合。
Alex 认为 group conv 的方式能够增加 filter 之间的对角相关性，而且能够减少训练参数，不容易过拟合，这类似于正则的效果。

空洞卷积（dilated convolution）是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野，让原本 3
x3 的卷积核，在相同参数量和计算量下拥有 5x5（dilated rate =2）或者更大的感受野，从而无需下采样。扩张卷积（dilated convolutions）又名空洞卷积（atrous convolutions），向卷积层引入了一个称为 “扩张率 (dilation rate)” 的新参数，该参数定义了卷积核处理数据时各值的间距。换句话说，相比原来的标准卷积，扩张卷积（dilated convolution） 多了一个 hyper-parameter（超参数）称之为 dilation rate（扩张率），指的是 kernel 各点之前的间隔数量，【正常的 convolution 的 dilatation rate 为 1】。

图说空洞卷积的概念

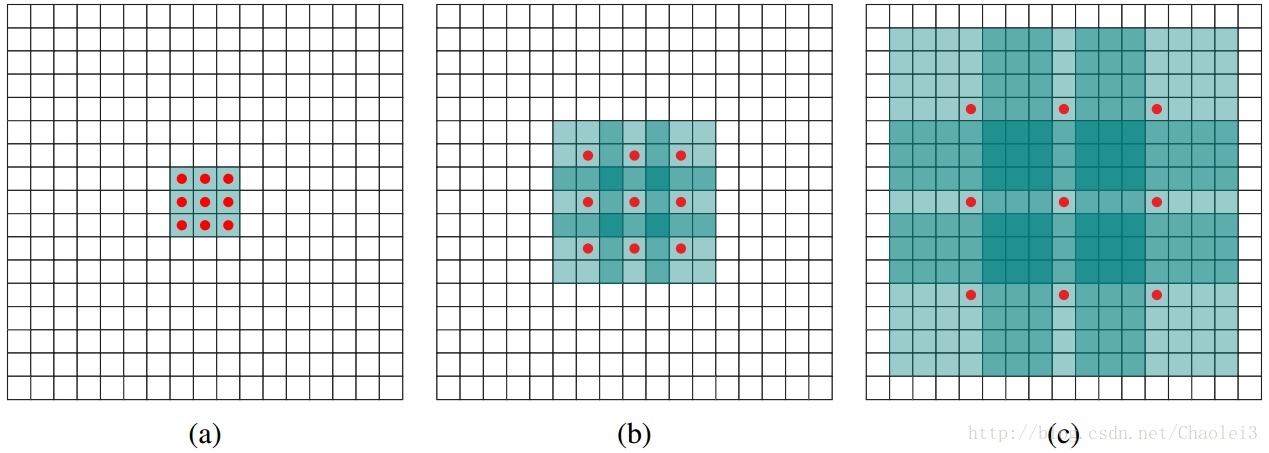
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图5

(a) 图对应 3x3 的 1-dilated conv，和普通的卷积操作一样。(b) 图对应 3x3 的 2-dilated conv，实际的卷积 kernel size 还是 3x3，但是空洞为 1，需要注意的是空洞的位置全填进去 0，填入 0 之后再卷积即可。【此变化见下图】（c）图是 4-dilated conv 操作。
在上图中扩张卷积的感受野可以由以下公式计算得到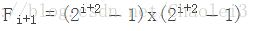对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图6
；其中 i+1 表示 dilated rate。
比如上图中（a），dilated=1，F(dilated) = 3×3；图（b）中，dilated=2，F(dilated)=7×7；图（c）中，dilated=4， F(dilated)=15×15。
dilated=2 时具体的操作，即按照下图在空洞位置填入 0 之后，然后直接卷积就可以了。
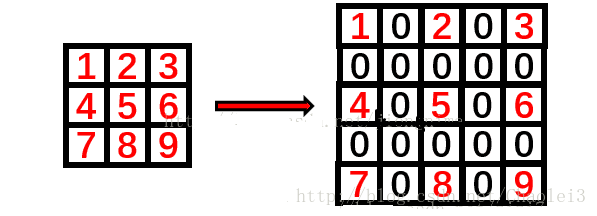
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图7

空洞卷积的动态过程

在二维图像上直观地感受一下扩张卷积的过程：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图8

上图是一个扩张率为 2 的 3×3 卷积核，感受野与 5×5 的卷积核相同，而且仅需要 9 个参数。你可以把它想象成一个 5×5 的卷积核，每隔一行或一列删除一行或一列。
在相同的计算条件下，空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野，但计算资源有限而无法提高卷积核数量或大小时，可以考虑空洞卷积。

Dilated Convolution 感受野指数级增长

对于标准卷积核情况，比如用 3×3 卷积核连续卷积 2 次，在第 3 层中得到 1 个 Feature 点，那么第 3 层这个 Feature 点换算回第 1 层覆盖了多少个 Feature 点呢？
第 3 层：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图9

第 2 层：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图10

第 1 层：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图11

第一层的一个 5×5 大小的区域经过 2 次 3×3 的标准卷积之后，变成了一个点。也就是说从 size 上来讲，2 层 33 卷积转换相当于 1 层 55 卷积。题外话，从以上图的演化也可以看出，一个 5×5 的卷积核是可以由 2 次连续的 3×3 的卷积代替。
但对于 dilated=2，3*3 的扩张卷积核呢？
第 3 层的一个点：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图12

第 2 层：
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图13

对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图14

可以看到第一层 13×13 的区域，经过 2 次 3×3 的扩张卷积之后，变成了一个点。即从 size 上来讲，连续 2 层的 3×3 空洞卷积转换相当于 1 层 13×13 卷积。

转置卷积（transposed Convolutions）又名反卷积（deconvolution）或是分数步长卷积（fractially straced convolutions）。反卷积（Transposed Convolution, Fractionally Strided Convolution or Deconvolution）的概念第一次出现是 Zeiler 在 2010 年发表的论文 Deconvolutional networks 中。

转置卷积和反卷积的区别

那什么是反卷积？从字面上理解就是卷积的逆过程。值得注意的反卷积虽然存在，但是在深度学习中并不常用。而转置卷积虽然又名反卷积，却不是真正意义上的反卷积。因为根据反卷积的数学含义，通过反卷积可以将通过卷积的输出信号，完全还原输入信号。而事实是，转置卷积只能还原 shape 大小，而不能还原 value。你可以理解成，至少在数值方面上，转置卷积不能实现卷积操作的逆过程。所以说转置卷积与真正的反卷积有点相似，因为两者产生了相同的空间分辨率。但是又名反卷积（deconvolutions）的这种叫法是不合适的，因为它不符合反卷积的概念。

转置卷积的动态图

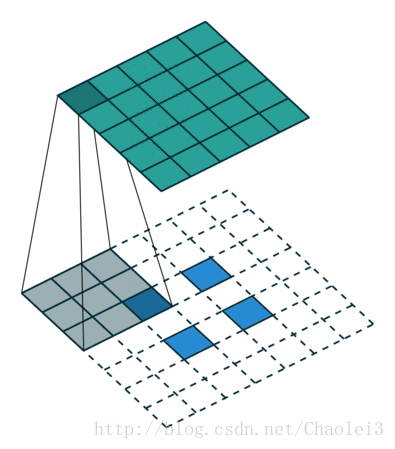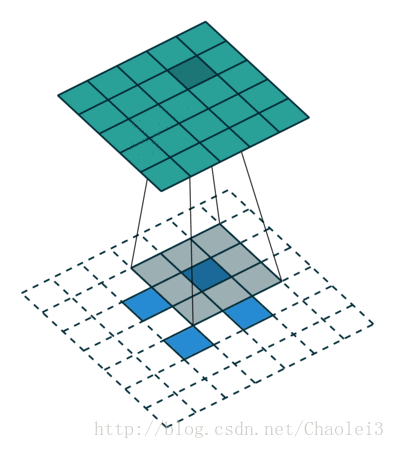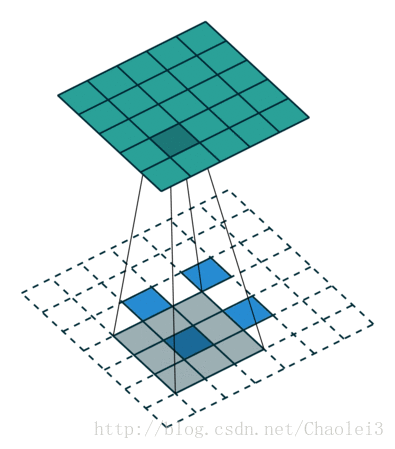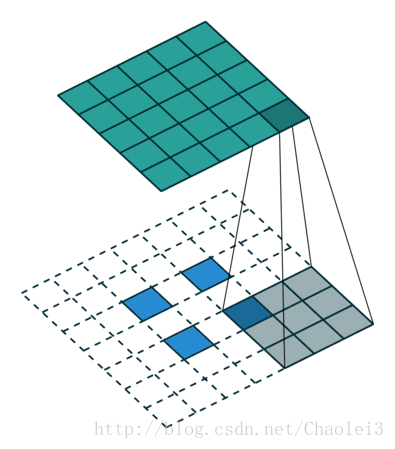
对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解 - 图15

△卷积核为 3×3、步幅为 2 和无边界扩充的二维转置卷积
需要注意的是，转置前后 padding，stride 仍然是卷积过程指定的数值，不会改变。

例子

由于上面只是理论的说明了转置卷积的目的，而并没有说明如何由卷积之后的输出重建输入。下面我们通过一个例子来说明感受下。
比如有输入数据：3×3，Reshape 之后，为 A ：1×9，B(可以理解为滤波器)：9×4(Toeplitz matrix) 那么 AB=C：1×4；Reshape C=2×2。所以，通过 B 卷积，我们从输入数据由 shape=3×3 变成了 shape=2×2。反过来。当我们把卷积的结果拿来做输入，此时 A：2×2,reshape 之后为 1×4，B 的转置为 4×9，那么 AB=C=1×9，注意此时求得的 C，我们就认为它是卷积之前的输入了，虽然存在偏差。然后 reshape 为 3×3。所以，通过 B 的转置 - “反卷积”，我们从卷积结果 shape=2×2 得到了 shape=3×3，重建了分辨率。
也就是输入 feature map A=[3,3]经过了卷积 B=[2,2] 输出为 [2,2] , 其中 padding=0,stride=1，反卷积（转置卷积）则是输入 feature map A=[2,2], 经过了反卷积滤波 B=[2,2]. 输出为[3,3]。其中 padding=0,stride=1 不变。那么[2,2]的卷积核 (滤波器) 是怎么转化为[4,9]或者[9,4]的呢？通过 Toeplitz matrix。
至于这其中 Toeplitz matrix 是个什么东西，此处限于篇幅就不再介绍了。但即使不知道这个矩阵，转置卷积的具体工作也应该能够明白的。
https://blog.csdn.net/Chaolei3/article/details/79374563