哈夫曼树

哈夫曼树的构造过程

首先生成一颗哈夫曼树，每次生成过程中选取频率最少的两个节点，生成一个新节点作为它们的父节点，并且新节点的频率为两个节点的和。选取频率最少的原因是，生成过程使得先选取的节点位于树的更低层，那么需要的编码长度更长，频率更少可以使得总编码长度更少。

生成编码时，从根节点出发，向左遍历则添加二进制位 0，向右则添加二进制位 1，直到遍历到叶子节点，叶子节点代表的字符的编码就是这个路径编码。

举例：

  • 给定了四个结点a，b，c，d，权值分别为7，5，2，4。
    image.png
  • 找出现有权值中最小的两个，2 和 4 ，相应的结点 c 和 d 构建一个新的二叉树，树根的权值为 2 + 4 = 6，同时将原有权值中的 2 和 4 删掉，将新的权值 6 加入。
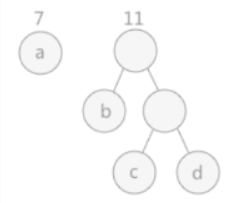
    image.png
  • 重复之前的步骤。image.png
  • 所有的结点构建成了一个全新的二叉树，这就是哈夫曼树。
    image.png

代码

  1. public class Huffman {
  3.     private class Node implements Comparable<Node> {
  4.         char ch;
  5.         int freq;
  6.         boolean isLeaf;
  7.         Node left, right;
  9.         public Node(char ch, int freq) {
  10.             this.ch = ch;
  11.             this.freq = freq;
  12.             isLeaf = true;
  13.         }
  15.         public Node(Node left, Node right, int freq) {
  16.             this.left = left;
  17.             this.right = right;
  18.             this.freq = freq;
  19.             isLeaf = false;
  20.         }
  22.         @Override
  23.         public int compareTo(Node o) {
  24.             return this.freq - o.freq;
  25.         }
  26.     }
  28.     public Map<Character, String> encode(Map<Character, Integer> frequencyForChar) {
  29.         PriorityQueue<Node> priorityQueue = new PriorityQueue<>();
  30.         for (Character c : frequencyForChar.keySet()) {
  31.             priorityQueue.add(new Node(c, frequencyForChar.get(c)));
  32.         }
  33.         while (priorityQueue.size() != 1) {
  34.             Node node1 = priorityQueue.poll();
  35.             Node node2 = priorityQueue.poll();
  36.             priorityQueue.add(new Node(node1, node2, node1.freq + node2.freq));
  37.         }
  38.         return encode(priorityQueue.poll());
  39.     }
  41.     private Map<Character, String> encode(Node root) {
  42.         Map<Character, String> encodingForChar = new HashMap<>();
  43.         encode(root, "", encodingForChar);
  44.         return encodingForChar;
  45.     }
  47.     private void encode(Node node, String encoding, Map<Character, String> encodingForChar) {
  48.         if (node.isLeaf) {
  49.             encodingForChar.put(node.ch, encoding);
  50.             return;
  51.         }
  52.         encode(node.left, encoding + '0', encodingForChar);
  53.         encode(node.right, encoding + '1', encodingForChar);
  54.     }
  55. }