最短路径

Dijkstra 单源最短路径算法

前提：图中不能有负权边

图中的蓝色顶点表示已加入最短路径树。红色的边就是最短路径。

图的右方左部分是索引堆，右部分是distTo[v] (表示从源点到v的已知最短路径长度)。

Dijkstra算法思路 ：

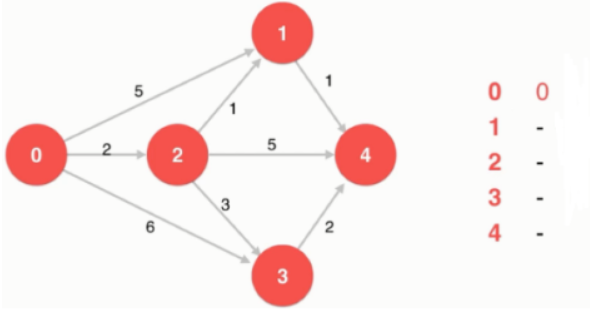
将0顶点开始，将访问顶点1、2、3

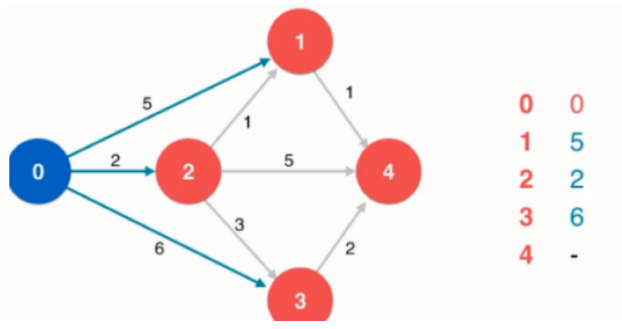
到没有访问过的顶点的最短路径是2，也就是顶点2

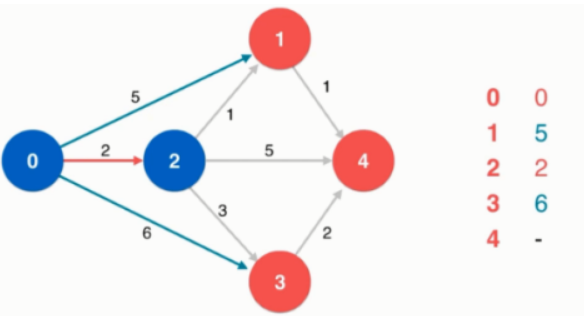
从2开始，将访问1、3、4。

先访问顶点 1 ，则0->2->1的路径就为3，此时不需要考虑0->1权为5的边了。

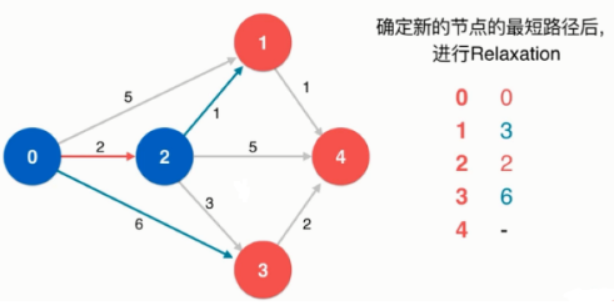
访问 顶点 4 ，则 0->2->4的路径长为7。

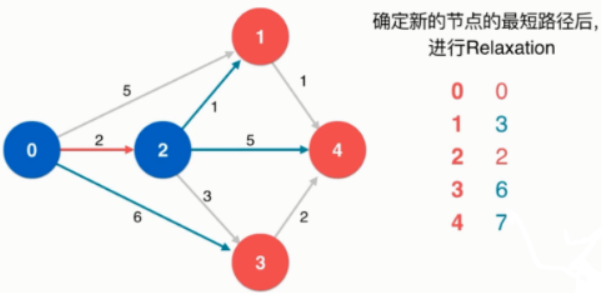
访问 顶点 3，则 0->2->3的路径长为5，此时就不需要考虑0->3权为6的边了。

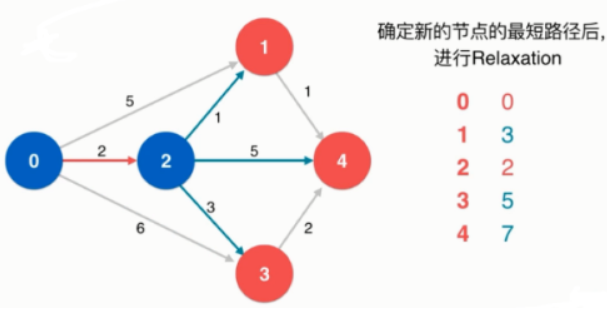
此时所能到达的最短路径是顶点1。

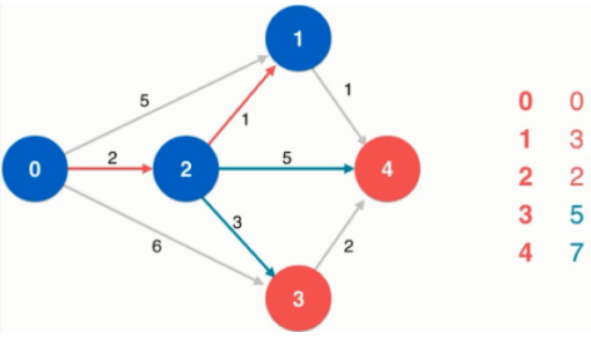
考虑顶点1的邻边，1->4的路径更小。

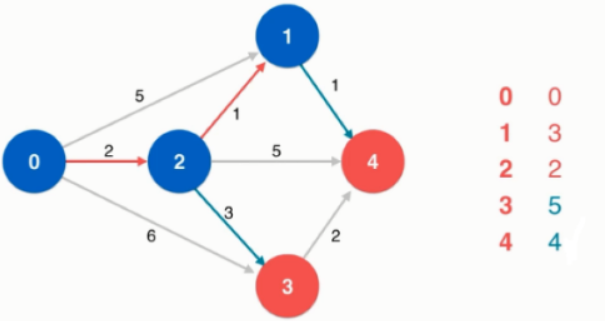
此时所能到达的最短路径是顶点4。

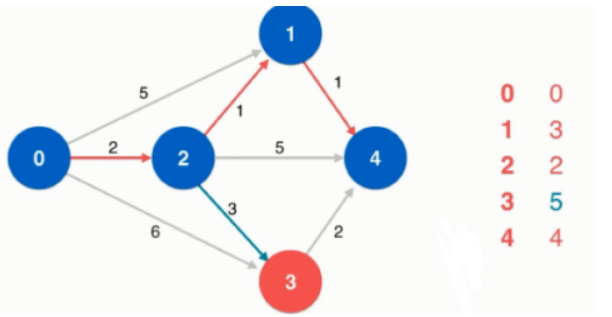
此时所能到达的最短路径是顶点3.

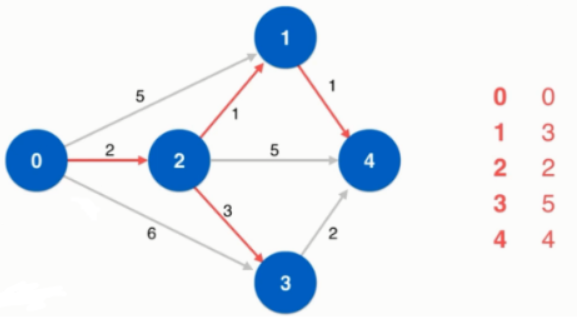
public class DijkstraSP<E extends Number & Comparable>{
    private WeightedGraph G;
    // 图的引用
    private int s;
    // 起始点
    private Number[] distTo;
    // distTo[i]存储从起始点s到顶点i的最短路径长度
    private boolean[] marked;
    // 标记数组, 在算法运行过程中标记节点i是否被访问
    private Edge<E>[] from;
    // from[i]记录最短路径中, 到达i点的边是哪一条
    // 可以用来恢复整个最短路径
    public DijkstraSP(WeightedGraph graph,int s){
        this.G=graph;
        this.s=s;
        distTo=new Number[G.V()];
        marked=new boolean[G.V()];
        from=new Edge[G.V()];
        //使用索引堆记录当前找到的到达每个顶点的最短距离 ---> Number类型
        IndexMinHeap<E> indexMinHeap=new IndexMinHeap<>(G.V());
        //初始化起始点
        distTo[s] = 0.0;
        from[s]=new Edge<E>(s,s,(E)((Number)0.0));
        marked[s]=true;
        indexMinHeap.insert(s,(E)distTo[s]);
        while (!indexMinHeap.isEmpty()){
            int v=indexMinHeap.extractMinIndex();
            // distTo[v]就是s到v的最短距离
            marked[v] = true;
            for(Object item:G.adj(v)){
                Edge<E> edge=(Edge<E>)item;
                int w=edge.other(v);
                //如果从s点到w点的最短路径还没有找到
                if(!marked[w]){
                    // 如果w点以前没有访问过,
                    // 或者访问过, 但是通过当前的v点到w点距离更短, 则进行更新
                    if(from[w]==null ||
                            (distTo[v].doubleValue()+edge.wt().doubleValue() < distTo[w].doubleValue())){
                        distTo[w]=distTo[v].doubleValue()+edge.wt().doubleValue();
                        from[w]=edge;
                        if(indexMinHeap.contain(w)){
                            indexMinHeap.change(w,(E)distTo[w]);
                        }else{
                            indexMinHeap.insert(w,(E)distTo[w]);
                        }
                    }
                }
            }
        }
    }
    //获取从s点到w点的最短路径长度
    public Number shortestPathTo(int w){
        assert hasPathTo(w);
        return distTo[w];
    }
    // 判断从s点到w点是否联通
    public boolean hasPathTo(int w){
        assert w>=0 && w<G.V();
        return marked[w];
    }
    //寻找从s到w的最短路径, 将整个路径经过的边存放在res中
    public Vector<Edge<E>> shortestPath(int w){
        assert hasPathTo(w);
        //通过from数组逆向查找到从s到w的路径, 存放到栈中
        Stack<Edge<E>> stack=new Stack<>();
        Edge<E> e=from[w];
        while (e.v()!=s){
            stack.push(e);
            e=from[e.v()];
        }
        //最后e.v()就是s,那么e这条边入栈
        stack.push(e);
        //从栈中依次取出元素, 获得顺序的从s到w的路径
        Vector<Edge<E>> res=new Vector<>();
        while (!stack.isEmpty()){
            Edge<E> edge=stack.pop();
            res.add(edge);
        }
        return res;
    }
    // 打印出从s点到w点的路径
    public void showPath(int w){
        assert hasPathTo(w);
        Vector<Edge<E>> path =  shortestPath(w);
        for( int i = 0 ; i < path.size() ; i ++ ){
            System.out.print( path.elementAt(i).v() + " -> ");
            if( i == path.size()-1 ){
                System.out.println(path.elementAt(i).w());
            }
        }
    }
}

Bellman-Ford 单源最短路径算法

1. 负权边问题

顶点0、1、2构成了一个负权环。

显然，有负权环的图，没有最短路径。

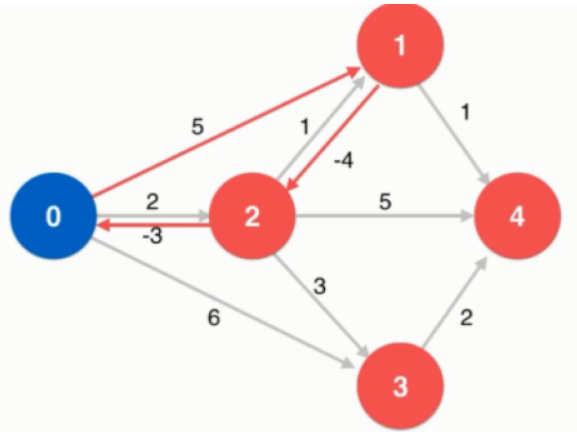
如果一个图没有负权环，从一点到另外一点的最短路径，
最多经过所有的V个顶点，有(V-1)条边。
否则，存在顶点经过了两次，也就是说存在负权环。

2. 思路

• 对一个顶点的一次松弛操作，就是找到经过这个点的另外一条路径，多一条边，权值更小。
• 如果一个图没有负权环，从一个顶点到另外一个顶点的最短路径，最多经过所有的V个顶点，有(V-1)条边。
• 对所有的点进行(V-1)次松弛操作，理论上可以找到到其他所有点的最短路径。
• 如果还可以继续松弛，说明原图中有负权环。

3. 实践

public BellmanFordSP(WeightedGraph graph,int s){
    this.G=graph;
    this.s=s;
    distTo=new Number[G.V()];
    marked=new boolean[G.V()];
    from=new Edge[G.V()];
    // // 设置distTo[s] = 0, 并且让from[s]不为NULL, 表示初始s节点可达且距离为0
    distTo[s] = 0.0;
    from[s] = new Edge<E>(s, s, (E)(Number)(0.0));
    // Bellman-Ford的过程
    // 进行V-1次循环, 每一次循环求出从起点到其余所有点, 最多使用pass步可到达的最短距离
    for(int pass=1;pass<G.V();pass++){
        // 每次循环中对所有的边进行一遍松弛操作
        // 遍历所有边的方式是先遍历所有的顶点, 然后遍历和所有顶点相邻的所有边
        for(int i=0;i<G.V();i++){
            for(Object item:G.adj(i)){
                Edge<E> e=(Edge<E>)item;
                // 对于每一个边首先判断e->v()可达
                // 之后看如果e->w()以前没有到达过， 显然我们可以更新distTo[e->w()]
                // 或者e->w()以前虽然到达过, 但是通过这个e我们可以获得一个更短的距离,
                // 即可以进行一次松弛操作, 我们也可以更新distTo[e->w()]
                if(from[e.v()]!=null &&
                        (from[e.w()]==null || distTo[e.v()].doubleValue()+e.wt().doubleValue()<distTo[e.w()].doubleValue())){
                    distTo[e.w()]=distTo[e.v()].doubleValue()+e.wt().doubleValue();
                    from[e.w()]=e;
                }
            }
        }
    }
}

4. 查看图中是否有负权环