| 底层结构 | 入队 | 出队(获取最大元素) |
|---|---|---|
| 普通线性结构 | O(1) | O(n) |
| 顺序线性结构 | O(n) | O(1) |
| 堆 | O(log n) | O(log n) |
堆
二叉堆的性质
- 二叉堆是一棵完全二叉树

- 堆中的某个结点值总是不大于其父节点的值
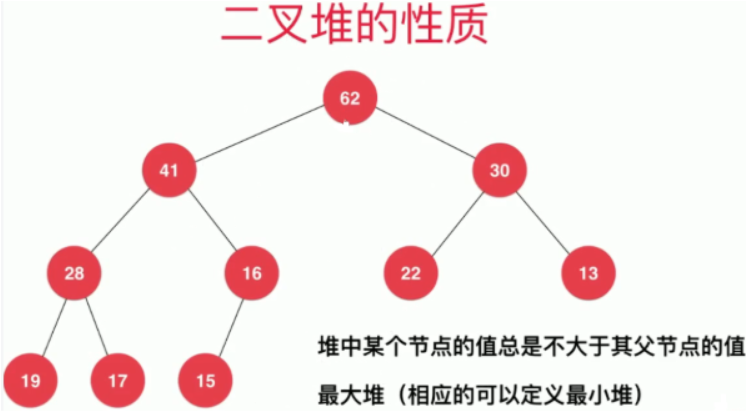
堆的基本结构
- 使用数组存储二叉堆,下标从1开始

- 使用数组存储二叉堆,下标从0开始
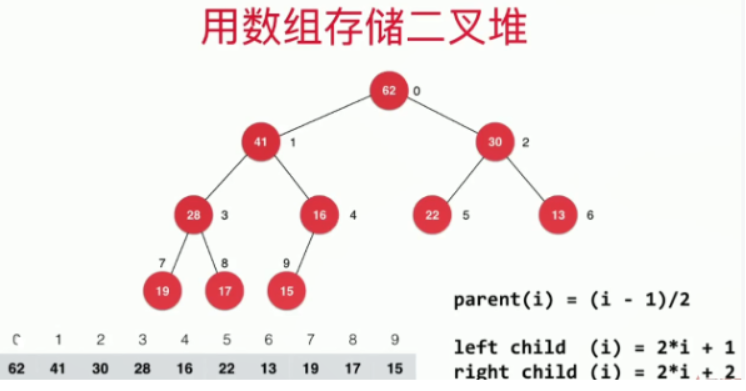
白板编程最大堆的一些准备工作:
public class MaxHeap<E extends Comparable<E>> {private E[] data;private int size;//记录堆中元素个数public MaxHeap(int capacity){data=(E[])new Comparable[capacity];}public MaxHeap(){this(10);}//返回堆中元素个数public int size(){return size;}//判断堆是否为空public boolean isEmpty(){return size==0;}//返回一个索引的父节点的索引private int parent(int index){if(index==0){throw new IllegalArgumentException("index-0 does not have parment");}return (index-1)/2;}//返回一个索引的左孩子节点的索引private int leftChild(int index){return 2*index+1;}//返回一个索引的左孩子节点的索引private int rightChild(int index){return 2*index+2;}private void swap(int i,int j){if(i<0 || i>=size || j<0 || j>=size){throw new IllegalArgumentException("Index is illegal");}E tmp=data[i];data[i]=data[j];data[j]=tmp;}//调整数组大小private void resize(int newCapacity){E[] newData=(E[])new Object[newCapacity];for(int i=0;i<size;i++){newData[i]=data[i];}data=newData;}}
添加元素和取出元素
- 向堆中添加元素和上浮操作
//向堆中添加元素//时间复杂度 O(log n)public void add(E e){if(size==data.length){resize(data.length*2);}data[size]=e;size++;swim(size-1);}//对索引为k的元素,进行上浮操作,得到一个新的最大堆private void swim(int k){while(k>0 && data[k].compareTo(data[parent(k)])>0){swap(k,parent(k));k=parent(k);}}
- 向堆中取出元素和下沉操作
//查看堆中最大元素public E findMax(){if(size==0){throw new IllegalArgumentException("Can not find max when maxheap is empty!");}return data[0];}//从堆中取出元素//时间复杂度O(log n)public E extractMax(){if(size==0){throw new IllegalArgumentException("MaxHeap is empty");}E ret=findMax();swap(0,size-1);size--;sink(0);return ret;}private void sink(int k){while (leftChild(k)<size){ //leftChild(k)<size 下标为k的元素存在左子树int j=leftChild(k);if(j+1<size &&data[j].compareTo(data[j+1])<0){j=j+1;}//j是data[leftChild(k)]和data[rightChild(k)]的较大值的下标if(data[k].compareTo(data[j])>=0){break;}swap(k,j);k=j;}}
replace和heapify
- replace:取出最大元素后,放入新元素
实现一:先extractMax(),再add(),两次O(log n)操作
实现二:直接替换堆顶元素,在进行下沉操作,一次O(log n)操作
//replace:取出最大元素后,放入新元素public E replace(E e){E ret=data[0];data[0]=e;sink(0);return ret;}
- heapify:将任意数组整理成堆的形状
将数组看成一颗完全二叉树,从该二叉树的最后一个分叶子节点开始,进行下沉操作。

//heapify:将任意数组整理成堆的形状public MaxHeap(E[] arr){data=(E[])new Comparable[arr.length];for(int i=0;i<arr.length;i++){data[i]=arr[i];}size=arr.length;for(int i=parent(arr.length-1);i>=0;i--){sink(i);}}
基于堆的优先队列
public class PriorityQueue<E extends Comparable<E>> implements Queue<E>{private MaxHeap<E> maxHeap;public PriorityQueue(){maxHeap=new MaxHeap<>();}@Overridepublic int getSize() {return maxHeap.size();}@Overridepublic boolean isEmpty() {return maxHeap.isEmpty();}@Overridepublic void enqueue(E e) {maxHeap.add(e);}@Overridepublic E dequeue() {return maxHeap.extractMax();}@Overridepublic E getFront() {return maxHeap.findMax();}}
Java中的PriorityQueue
LeetCode 347 Top K Frequent Elements
private class Pair implements Comparable<Pair> {int numFreq;int num;Pair(int numFreq,int num){this.numFreq=numFreq;this.num=num;}@Overridepublic int compareTo(Pair o) {return this.numFreq-o.numFreq;}}public List<Integer> topKFrequent(int[] nums, int k) {//统计数字出现的频率Map<Integer,Integer> map=new HashMap<>();for(int num:nums){int freq=map.get(num)==null?0:map.get(num);map.put(num,++freq);}//维护一个优先队列,最小堆,维护当前频率最高的元素PriorityQueue<Pair> priorityQueue=new PriorityQueue<>();//pair存的是(频率,元素)的形式for(Integer num:map.keySet()){int numFreq=map.get(num);if(priorityQueue.size()==k){if(numFreq>priorityQueue.peek().numFreq){priorityQueue.poll();priorityQueue.add(new Pair(numFreq,num));}}else{priorityQueue.add(new Pair(numFreq,num));}}List<Integer> ret=new ArrayList<>();while(!priorityQueue.isEmpty()){ret.add(priorityQueue.poll().num);}return ret;}
使用匿名比较器对象改进:
public List<Integer> topKFrequent(int[] nums, int k) {//统计数字出现的频率Map<Integer,Integer> map=new HashMap<>();for(int num:nums){int freq=map.get(num)==null?0:map.get(num);map.put(num,++freq);}//维护一个优先队列,最小堆,维护当前频率最高的元素PriorityQueue<Integer> priorityQueue=new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer a, Integer b) {return map.get(a)-map.get(b);}});//pair存的是(频率,元素)的形式for(Integer num:map.keySet()){priorityQueue.add(num);if(priorityQueue.size()>k) {priorityQueue.poll();}}List<Integer> ret=new ArrayList<>();while(!priorityQueue.isEmpty()){ret.add(priorityQueue.poll());}Collections.reverse(ret);return ret;}

