线性结构是最简单,也是最常用的数据结构之一。线性结构的特点是:在数据元素的有限集中,除第一个元素无直接前驱,最后一个元素无直接后继以外,每个数据元素有且仅有一个直接前驱元素和一个直接后续元素。
数组
/*** 二次封装属于我们自己的数组的准备工作*/public class Array {private int[] data;private int size;public Array(int capacity){data=new int[capacity];size=0;}//无参构造函数,默认数组的容量是10public Array(){this(10);}public int getSize(){return size;}public int getCapacity(){return data.length;}public boolean isEmpty(){return size==0;}@Overridepublic String toString(){StringBuilder builder=new StringBuilder();builder.append(String.format("Array size=%d,capacity=%d\n",size,data.length));builder.append("[");for(int i=0;i<size;i++){builder.append(data[i]);if(i!=size-1){builder.append(", ");}}builder.append("]");return builder.toString();}}
添加元素
//在所有元素后添加新元素public void addLast(int e) {//要先判断是否有空间来容纳新元素/*if(size==data.length){throw new IllegalArgumentException("AddLast failed,array is full");}data[size]=e;size++;*/add(size,e);}//在所有元素前添加新元素public void addFirst(int e){add(0,e);}//在index位置插入元素public void add(int index,int e){if(size==data.length){throw new IllegalArgumentException("Add failed,array is full");}if(index<0 || index>size){throw new IllegalArgumentException("Add Failed,0<=index<=size is required");}//index位置后的元素向右移动for(int i=size;i>index;i--){data[i]=data[i-1];}data[index]=e;size++;}
查询元素
//获取index位置的元素public int get(int index){if(index<0 || index>=size){throw new IllegalArgumentException("Get failed,index is illegal");}return data[index];}
//查找数组中是否有元素e,有就返回下标,没有就返回-1public boolean contains(int e){for(int i=0;i<size;i++){if(data[i]==e){return true;}}return false;}//查找数组中元素e所在索引public int find(int e){for(int i=0;i<size;i++){if(data[i]==e){return i;}}return -1;}
修改元素
//设置index位置元素值为epublic void set(int index,int e){if(index<0 || index>=size){throw new IllegalArgumentException("Get failed,index is illegal");}data[index]=e;}
删除元素
//删除指定位置元素public int remove(int index){if(size==0){throw new IllegalArgumentException("Remove failed,array is empty");}if(index<0 || index>=size){throw new IllegalArgumentException("Remove failed,index is illegal");}int ret=data[index];for(int i=index+1;i<size;i++){data[i-1]=data[i];}size--;return ret;}public int removeFirst(){return remove(0);}public int removeLast(){return remove(size-1);}public void removeElement(int e){int index=find(e);if(index!=-1){remove(index);}}
动态数组
调整数组大小
思路
- 准备一个新数组,长度是原来数组的2倍
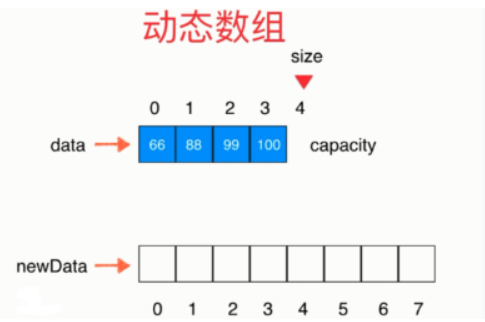
- 将原来数组中的元素复制到新数组中
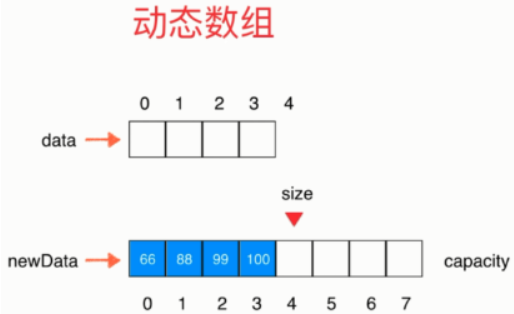
- 将data指向newData,完成扩容
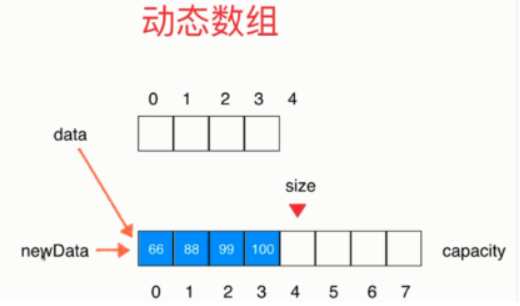
- 完成扩容,capacity是原来的2倍,size不变,数组中数据不变
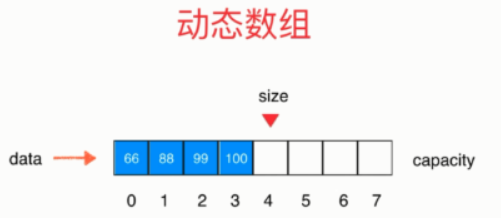
代码
//动态调整数组大小private void resize(int newCapacity){E[] newData=(E[])new Object[newCapacity];for(int i=0;i<size;i++){newData[i]=data[i];}data=newData;}
添加元素
//在index位置插入元素public void add(int index,E e){/* if(size==data.length){throw new IllegalArgumentException("Add failed,array is full");}*/if(size==data.length){resize(data.length*2);}if(index<0 || index>size){throw new IllegalArgumentException("Add Failed,0<=index<=size is required");}//index位置后的元素向右移动for(int i=size;i>index;i--){data[i]=data[i-1];}data[index]=e;size++;}
删除元素
//删除指定位置元素public int remove(int index){/*if(size==0){throw new IllegalArgumentException("Remove failed,array is empty");}*/if(size==data.length/2){resize(data.length/2);}if(index<0 || index>=size){throw new IllegalArgumentException("Remove failed,index is illegal");}E ret=data[index];for(int i=index+1;i<size;i++){data[i-1]=data[i];}size--;data[size]=null;//loitering objectsreturn ret;}
addLast() 时间复杂度分析
假设 capacity=n,(n+1)次进行 addLast 操作,会触发 resize,总共进行(2*n+1)次基本操作。
平均情况下,每次 addLast 操作,进行 2 次基本操作。这样均摊计算,时间复杂度是 O(1)。所以addLast的均摊复杂度是 O(1)。同理,removeLast 的均摊复杂度是O(1)。
复杂度震荡
capcity 为 n,此时 size=n:
进行 addLast() 操作,由于需要 resize(),时间复杂度为 O(n);
再进行 removeLast() 操作,由于需要 resize(),时间复杂度为 O(n);
再进行 addLast() 操作,由于需要 resize(),时间复杂度为 O(n)
…
这就是复杂度震荡。
解决复杂度震荡的方法:lazy,即在 size==capacity/4,才将 capacity 减半。
//删除指定位置元素public int remove(int index){/*if(size==0){throw new IllegalArgumentException("Remove failed,array is empty");}*//* if(size==data.length/2){resize(data.length/2);}*/if(size==data.length/4 && data.length/2!=0){resize(data.length/2);}if(index<0 || index>=size){throw new IllegalArgumentException("Remove failed,index is illegal");}E ret=data[index];for(int i=index+1;i<size;i++){data[i-1]=data[i];}size--;//data[size]=null;//loitering objects,使用泛型时,进行此操作return ret;}
时间复杂度分析
| 操作 | 时间复杂度 |
|---|---|
| 添加操作 | 平均时间复杂度:O(n) |
| addLast(e) | O(1) |
| addFirst(e) | O(n) |
| add(index) | O(n) |
| 删除操作 | 平均时间复杂度:O(n) |
| removeLast(e) | O(1) |
| removeFirst(e) | O(n) |
| remove(index,e) | O(n) |
| 修改操作 | |
| set(index,e) | O(1) |
| 查找操作 | |
| get(index) | O(1) |
| contains(e) | O(n) |
| find(e) | O(n) |
链表
链表结点
/*** 链表结点*/public class Node<E> {public E e;public Node next;public Node(E e, Node next){this.e=e;this.next=next;}public Node(E e){this(e,null);}public Node(){this(null,null);}@Overridepublic String toString() {return e.toString();}}
public class LinkedList<E> {private Node head;private int size;public LinkedList(){head=null;size=0;}public boolean isEmpty(){return size==0;}public int getSize(){return size;}@Overridepublic String toString() {StringBuilder builder=new StringBuilder();Node cur=dummyHead.next;while(cur!=null){builder.append(cur+"->");cur=cur.next;}builder.append("NULL");return builder.toString();}}
插入元素
在链表头插入元素
//在链表头添加元素public void addFirst(E e){Node node=new Node(e);node.next=head;head=node;size ++;}
在链表中间插入元素
//在链表index位置[从0开始]插入元素//这项操作在链表中并不常用public void add(int index,E e){if(index<0 || index>=size){throw new IllegalArgumentException("Index is illegal");}if(index==0){addFirst(e);}else{Node prev=head;for(int i=0;i<index-1;i++){prev=prev.next;}Node node=new Node(e);node.next=prev.next;prev.next=node;size ++;}}
虚拟头结点
public LinkedList(){dummyHead=new Node(null,null);size=0;}//在链表index位置[从0开始]插入元素//这项操作在链表中并不常用public void add(int index,E e){if(index<0 || index>size){throw new IllegalArgumentException("Index is illegal");}Node prev=dummyHead;for(int i=0;i<index;i++){prev=prev.next;}Node node=new Node(e);node.next=prev.next;prev.next=node;size++;}//在链表头添加元素public void addFirst(E e){add(0,e);}public void addLast(E e){add(size,e);}
查询元素
//获取链表index位置[从0开始]元素//这项操作在链表中并不常用public E get(int index){if(index<0 || index>=size){throw new IllegalArgumentException("Index is illegal");}Node cur=dummyHead.next;for(int i=0;i<index;i++){cur=cur.next;}return (E)cur.e;}public E getFirst(){return get(0);}public E getLast(){return get(size-1);}
//查找链表中是否有元素epublic boolean contains(E e){Node cur=dummyHead.next;while(cur!=null){if(cur.e.equals(e)){return true;}cur=cur.next;}return false;}
修改元素
//修改链表index位置[从0开始]元素public void set(int index,E e){if(index<0 || index>=size){throw new IllegalArgumentException("Index is illegal");}Node cur=dummyHead.next;for(int i=0;i<index;i++){cur=cur.next;}cur.e=e;}
删除元素
//删除链表index位置[从0开始]元素public E remove(int index){if(index<0 || index>=size){throw new IllegalArgumentException("Index is illegal");}Node prev=dummyHead;for(int i=0;i<index;i++){prev=prev.next;}Node delNode= prev.next;prev.next=delNode.next;delNode.next=null;size--;return (E)delNode.e;}public E removeFirst(){return remove(0);}public E removeLast(){return remove(size-1);}
时间复杂度分析
| 操作 | 时间复杂度 |
|---|---|
| 添加操作 | 平均时间复杂度:O(n) |
| addlast() | O(n) |
| addFirst() | O(1) |
| add(index,e) | O(n/2)=O(n) |
| 删除操作 | 平均时间复杂度:O(n) |
| removeLast() | O(n) |
| removeFirst() | O(1) |
| remove(index,e) | O(n/2)=O(n) |
| 修改操作 | O(n) |
| set(index,e) | O(n) |
| 查找操作 | O(n) |
| get(index) | O(n) |
| contains(e) | O(n) |

