二叉搜索树（BST）

image.png

BST 的基本功能

  1. public class BST<E extends Comparable<E>> {
  2.     private Node root;
  3.     private int size;
  5.     public BST(){
  6.         root=null;
  7.         size=0;
  8.     }
  10.     public int size(){
  11.         return size;
  12.     }
  14.     public boolean isEmpty(){
  15.         return size==0;
  16.     }
  18.     private class Node{
  19.         public E e;
  20.         public Node left,right;
  21.         public Node(E e){
  22.             this.e=e;
  23.             this.left=null;
  24.             this.right=null;
  25.         }
  26.     }
  27. }

添加元素

思路

  • 对于如下的 BST，向其中添加 28：

image.png

  • 28 与根结点 41 比较，应该插入左子树

image.png

  • 28 与左子树的根结点 22 比较，应该插入该结点的右子树

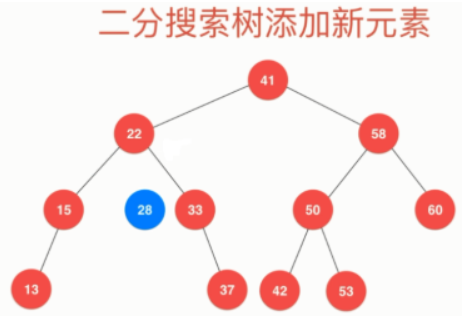
image.png

  • 28 与 33 比较，应该插入该结点的左子树，该结点的左子树为空，则将值为 28 的结点添加到该结点的左子树中

image.png

  • 最终将 28 添加到该 BST 中

image.png

代码

  1. //向BST中添加新元素e
  2. public void add(E e){
  3.     if(root==null){
  4.         root=new Node(e);
  5.         size++;
  6.         return;
  7.     }else{
  8.         add(root,e);
  9.     }
  10. }
  12. //向以node为根节点的BST树种插入元素e
  13. private void add(Node node,E e){
  14.     if(e.equals(node.e)){
  15.         //插入元素与根节点相等，直接返回
  16.         return;
  17.     }else if(e.compareTo(node.e)<0 && node.left==null){
  18.         node.left=new Node(e);
  19.         size++;
  20.         return;
  21.     }else if(e.compareTo(node.e)>0 && node.right==null){
  22.         node.right=new Node(e);
  23.         size++;
  24.         return;
  25.     }
  26.     if(e.compareTo(node.e)<0){
  27.         add(node.left,e);
  28.     }else{ //e.compareTo(node.e)>0
  29.         add(node.right,e);
  30.     }
  31. }

改进添加元素

前文中的添加操作，对 root==null 的情况进行了特殊处理,并且 add(Node,E) 中的递归条件也太冗长了。
这里我们写一个 add() 方法，返回插入新节点后该 BST 的根节点

  1. //向BST中添加新元素e
  2. public void add(E e){
  3.     root=add(root,e);
  4. }
  6. //向以node为根节点的BST树种插入元素e
  7. //返回插入新元素后该BST的根
  8. private Node add(Node node,E e){
  9.     if(node==null){
  10.         size++;
  11.         return new Node(e);
  12.     }
  13.     //注意：对于e.equals(node.e)不做处理
  14.     if(e.compareTo(node.e)<0){
  15.         node.left=add(node.left,e);
  16.     }else if(e.compareTo(node.e)>0){
  17.         node.right=add(node.right,e);
  18.     }
  19.     return node;
  20. }

查询元素

  1. //查看BST中是否包含元素e
  2. public boolean contains(E e){
  3.     return contains(root,e);
  4. }
  6. //查看以node为根节点的BST中是否包含元素e
  7. private boolean contains(Node node,E e){
  8.     if(node==null){
  9.         return false;
  10.     }
  11.     if(e.compareTo(node.e)==0){
  12.         return true;
  13.     }else if(e.compareTo(node.e)<0){
  14.         return contains(node.left,e);
  15.     }else{
  16.         return contains(node.right,e);
  17.     }
  18. }

遍历元素（递归形式）

  • 前序遍历
  1. //BST的前序遍历
  2. public void preOrder(){
  3.     preOrder(root);
  4. }
  6. private void preOrder(Node node){
  7.     if(node==null){
  8.         return;
  9.     }
  10.     System.out.println(node.e);
  11.     preOrder(node.left);
  12.     preOrder(node.right);
  13. }
  1. /**
  2. * 利用前序遍历打印 BST
  3. */
  4. @Override
  5. public String toString() {
  6.     StringBuilder res=new StringBuilder();
  7.     generateBST(root,0,res);
  8.     return res.toString();
  9. }
  11. //生成以node为根节点，深度为depth的描述二叉树的字符串（利用前序遍历）
  12. private void generateBST(Node node,int depth,StringBuilder res){
  13.     if(node==null){
  14.         res.append(generateDepth(depth)+"null\n");
  15.         return;
  16.     }
  17.     res.append(generateDepth(depth)+node.e+"\n");
  18.     generateBST(node.left,depth+1,res);
  19.     generateBST(node.right,depth+1,res);
  20. }
  22. private String generateDepth(int depth){
  23.     StringBuilder res=new StringBuilder();
  24.     for(int i=0;i<depth;i++){
  25.         res.append("--");
  26.     }
  27.     return res.toString();
  28. }
  • 中序遍历
  1. //BST的中序遍历
  2. public void inOrder(){
  3.     inOrder(root);
  4. }
  6. private void inOrder(Node node){
  7.     if(node==null){
  8.         return;
  9.     }
  10.     inOrder(node.left);
  11.     System.out.println(node.e);
  12.     inOrder(node.right);
  13. }
  • 后序遍历
  1. //BST的后序遍历
  2. public void postOrder(){
  3.     postOrder(root);
  4. }
  6. private void postOrder(Node node){
  7.     if(node==null){
  8.         return;
  9.     }
  10.     postOrder(node.left);
  11.     postOrder(node.right);
  12.     System.out.println(node.e);
  13. }

遍历元素（非递归形式）

  1. //枚举命令，GO表示访问元素，COUT表示打印元素
  2. private enum Command{GO,COUT};
  4. private class StackNode{
  5.     Command command;
  6.     Node node;
  7.     StackNode(Command command,Node node){
  8.         this.command=command;
  9.         this.node=node;
  10.     }
  11. }
  • 前序遍历
  1. //BST的前序遍历（非递归方式）
  2. public void preOrderNR(){
  3.     preOrderNR(root);
  4. }
  6. private void preOrderNR(Node node){
  7.     if(node==null){
  8.         return;
  9.     }
  10.     Stack<StackNode> stack=new Stack<>();
  11.     stack.push(new StackNode(Command.GO,node));
  12.     while(!stack.isEmpty()){
  13.         StackNode stackNode=stack.pop();
  14.         Node n=stackNode.node;
  15.         Command command=stackNode.command;
  16.         if(command==Command.COUT){
  17.             System.out.println(stackNode.node.e);
  18.         }else{
  19.             if(n.right!=null){
  20.                 stack.push(new StackNode(Command.GO,n.right));
  21.             }
  22.             if(n.left!=null){
  23.                 stack.push(new StackNode(Command.GO,n.left));
  24.             }
  25.             stack.push(new StackNode(Command.COUT,n));
  26.         }
  27.     }
  28. }
  • 中序遍历
  1. //BST的中序遍历（非递归方式）
  2. public void inOrderNR(){
  3.     inOrderNR(root);
  4. }
  6. private void inOrderNR(Node node){
  7.     if(node==null){
  8.         return;
  9.     }
  10.     Stack<StackNode> stack=new Stack<>();
  11.     stack.push(new StackNode(Command.GO,node));
  12.     while(!stack.isEmpty()){
  13.         StackNode stackNode=stack.pop();
  14.         Node n=stackNode.node;
  15.         Command command=stackNode.command;
  16.         if(command==Command.COUT){
  17.             System.out.println(stackNode.node.e);
  18.         }else{
  19.             if(n.right!=null){
  20.                 stack.push(new StackNode(Command.GO,n.right));
  21.             }
  22.             stack.push(new StackNode(Command.COUT,n));
  23.             if(n.left!=null){
  24.                 stack.push(new StackNode(Command.GO,n.left));
  25.             }
  26.         }
  27.     }
  28. }
  • 后序遍历
  1. //BST的后序遍历（非递归方式）
  2. public void postOrderNR(){
  3.     postOrderNR(root);
  4. }
  6. private void postOrderNR(Node node){
  7.     if(node==null){
  8.         return;
  9.     }
  10.     Stack<StackNode> stack=new Stack<>();
  11.     stack.push(new StackNode(Command.GO,node));
  12.     while(!stack.isEmpty()){
  13.         StackNode stackNode=stack.pop();
  14.         Node n=stackNode.node;
  15.         Command command=stackNode.command;
  16.         if(command==Command.COUT){
  17.             System.out.println(stackNode.node.e);
  18.         }else{
  19.             stack.push(new StackNode(Command.COUT,n));
  20.             if(n.right!=null){
  21.                 stack.push(new StackNode(Command.GO,n.right));
  22.             }
  23.             if(n.left!=null){
  24.                 stack.push(new StackNode(Command.GO,n.left));
  25.             }
  26.         }
  27.     }
  28. }

层序遍历

  1. //BST的层序遍历
  2. public void levelOrder(){
  3.     Queue<Node> q=new LinkedList<>();
  4.     q.add(root);
  5.     while(!q.isEmpty()){
  6.         Node node=q.remove();
  7.         System.out.println(node.e);
  8.         if(node.left!=null){
  9.             q.add(node.left);
  10.         }
  11.         if(node.right!=null){
  12.             q.add(node.right);
  13.         }
  14.     }
  15. }

删除元素

删除最小值和最大值

  • 寻找 BST 中的最小元素和最大元素
  1. //寻找BST中的最小元素
  2. public E min(){
  3.     if(size==0){
  4.         throw new IllegalArgumentException("BST is emmpty");
  5.     }
  6.     return min(root).e;
  7. }
  9. private Node min(Node node){
  10.     if(node.left==null){
  11.         return node;
  12.     }
  13.     return min(node.left);
  14. }
  16. //寻找BST中的最大元素
  17. public E max(){
  18.     if(size==0){
  19.         throw new IllegalArgumentException("BST is emmpty");
  20.     }
  21.     return max(root).e;
  22. }
  24. private Node max(Node node){
  25.     if(node.right==null){
  26.         return node;
  27.     }
  28.     return max(node.right);
  29. }
  • 删除BST中的最大值和最小值
    情况一：最小值是叶子节点。直接删除该节点
    image.png

情况二：最小值有右子树。删除该节点，再将该节点的右子树连接到原来的 BST 中

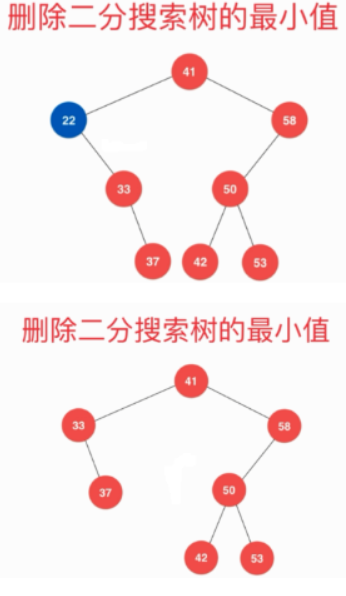
image.png

  • 代码：
  1. //删除BST中的最小值
  2. public E delMin(){
  3.     E res=min();
  4.     delMin(root);
  5.     return res;
  6. }
  8. //删除以node为根结点的BST中的最小值元素
  9. //这里考虑最小值只有右子树的情况，因为叶子节点是其特例
  10. private Node delMin(Node node){
  11.     if(node.left==null){
  12.         Node nodeRight=node.right;
  13.         node.right=null;
  14.         size--;
  15.         return nodeRight;
  16.     }
  17.     node.left=delMin(node.left);
  18.     return node;
  19. }
  21. //删除BST中的最大值
  22. public E delMax(){
  23.     E res=max();
  24.     delMax(root);
  25.     return res;
  26. }
  28. //删除以node为根结点的BST中的最大值元素
  29. private Node delMax(Node node){
  30.     if(node.right==null){
  31.         Node nodeLeft=node.left;
  32.         node.left=null;
  33.         size--;
  34.         return nodeLeft;
  35.     }
  36.     node.right=delMax(node.right);
  37.     return node;
  38. }

删除任意元素

  • 删除只有左孩子的节点。直接删除即可

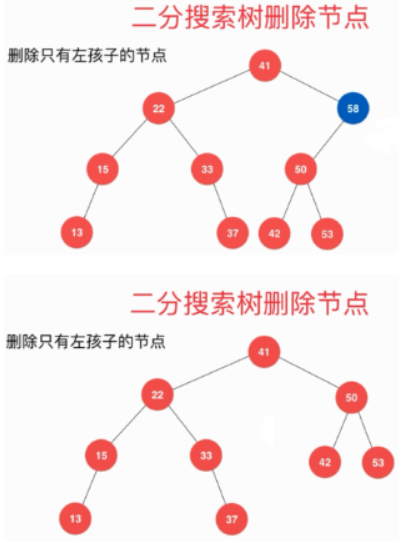
image.png

  • 删除只有右孩子的节点。直接删除即可

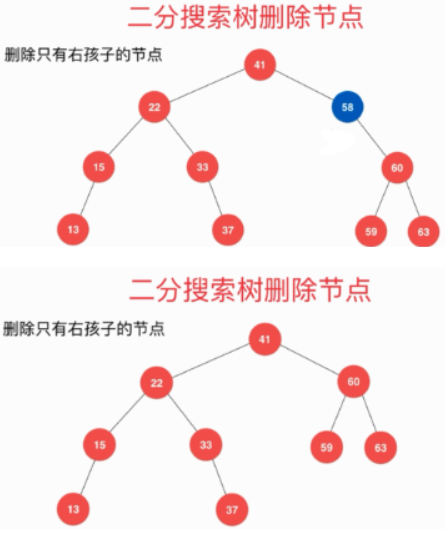
image.png

  • 删除左右孩子都有的节点

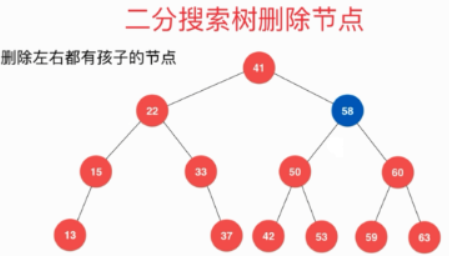
image.png

Habbard-Deletion：

d 是待删除的节点，s 节点是 d 的后继，也就是 d 的右子树的最小值所在的节点。

注意：这里选择左子树的最大值所在的节点效果也是相同的。

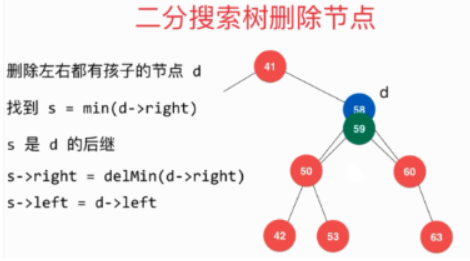
image.png

使用 s 代替 d

image.png

最后删除 d 节点

  • 代码
  1. //删除BST中任意元素
  2. public void del(E e){
  3.     root=del(root,e);
  4. }
  7. private Node del(Node node,E e){
  8.     if(node==null){
  9.         return null;
  10.     }
  11.     if(e.compareTo(node.e)<0){
  12.         node.left=del(node.left,e);
  13.         return node;
  14.     }else if(e.compareTo(node.e)>0){
  15.         node.right=del(node.right,e);
  16.         return node;
  17.     }else{
  18.         //节点node就是要删除的节点
  19.         //该节点只右有子树
  20.         if(node.left==null){
  21.             Node rightNode=node.right;
  22.             node.right=null;
  23.             size--;
  24.             return rightNode;
  25.         }
  26.         //该节点只有左子树
  27.         if(node.right==null){
  28.             Node leftNode=node.left;
  29.             node.left=null;
  30.             size--;
  31.             return leftNode;
  32.         }
  33.         //删除既有左子树又有右子树的节点
  34.         Node s=min(node.right);
  35.         s.right=delMin(node.right);
  36.         s.left=node.left;
  38.         //删除node
  39.         node.left=node.right=null;
  40.         return s;
  41.     }
  42. }